Angular momentum of a planet about the point of it's apogee is
Maximum when the planet is at perigee.
Maximum when the planet is at apogee.
Maximum when the planet is at end parts of the minor axis of the ellipse.
Maximum when the planet is at the end polats of the minor axis.
To solve the problem of finding the angular momentum of a planet about the point of its apogee, we can follow these steps:
Step 1: Understand the Definitions
- Apogee: The point in the orbit of a planet where it is farthest from the body it is orbiting.
- Perigee: The point in the orbit of a planet where it is closest to the body it is orbiting.
- Angular Momentum (L): The angular momentum of an object can be expressed as L=m⋅v⋅r, where m is the mass, v is the tangential velocity, and r is the distance from the point of rotation.
Step 2: Identify the Relevant Points
- The problem states that we need to find the angular momentum about the point of the apogee.
- The maximum distance r from the center of the planet (the body being orbited) occurs at the perigee.
Step 3: Analyze Angular Momentum at Apogee
- At the apogee, the distance r is the distance from the apogee point to the center of the planet.
- The velocity v of the planet is lower at the apogee compared to the perigee due to the conservation of angular momentum.
Step 4: Conclusion on Angular Momentum
- Since angular momentum is dependent on both the distance r and the velocity v, the angular momentum will be maximum when the planet is at the perigee, where r is minimized and v is maximized.
- Therefore, the angular momentum of the planet about the point of its apogee is maximum when the planet is at perigee.
Final Answer
The angular momentum of a planet about the point of its apogee is maximum when the planet is at its perigee.
---
- Apogee: The point in the orbit of a planet where it is farthest from the body it is orbiting.
- Perigee: The point in the orbit of a planet where it is closest to the body it is orbiting.
- Angular Momentum (L): The angular momentum of an object can be expressed as L=m⋅v⋅r, where m is the mass, v is the tangential velocity, and r is the distance from the point of rotation.
- The problem states that we need to find the angular momentum about the point of the apogee.
- The maximum distance r from the center of the planet (the body being orbited) occurs at the perigee.
- At the apogee, the distance r is the distance from the apogee point to the center of the planet.
- The velocity v of the planet is lower at the apogee compared to the perigee due to the conservation of angular momentum.
- Since angular momentum is dependent on both the distance r and the velocity v, the angular momentum will be maximum when the planet is at the perigee, where r is minimized and v is maximized.
- Therefore, the angular momentum of the planet about the point of its apogee is maximum when the planet is at perigee.
The angular momentum of a planet about the point of its apogee is maximum when the planet is at its perigee.
Similar Questions
Angular momentum is
View SolutionAngular momentum is
View SolutionAngular momentum is
View SolutionA: The speed of a planet is maximum at perihelion .
R : The angular momentum of a planet about centre of sun is conserved .
View SolutionSTATEMENT-1 : Assuming sun to be a body of very large mass in comparison to all other planets, the angular momentum of all the planets about the sun remains conserved.
because
STATEMENT-2 : Gravitational force is always conservative.
View SolutionWhen a body is projected at an angle with the horizontal in the uniform gravitational field of the earth, the angular momentum of the body about the point of projection, as it proceeds along its path
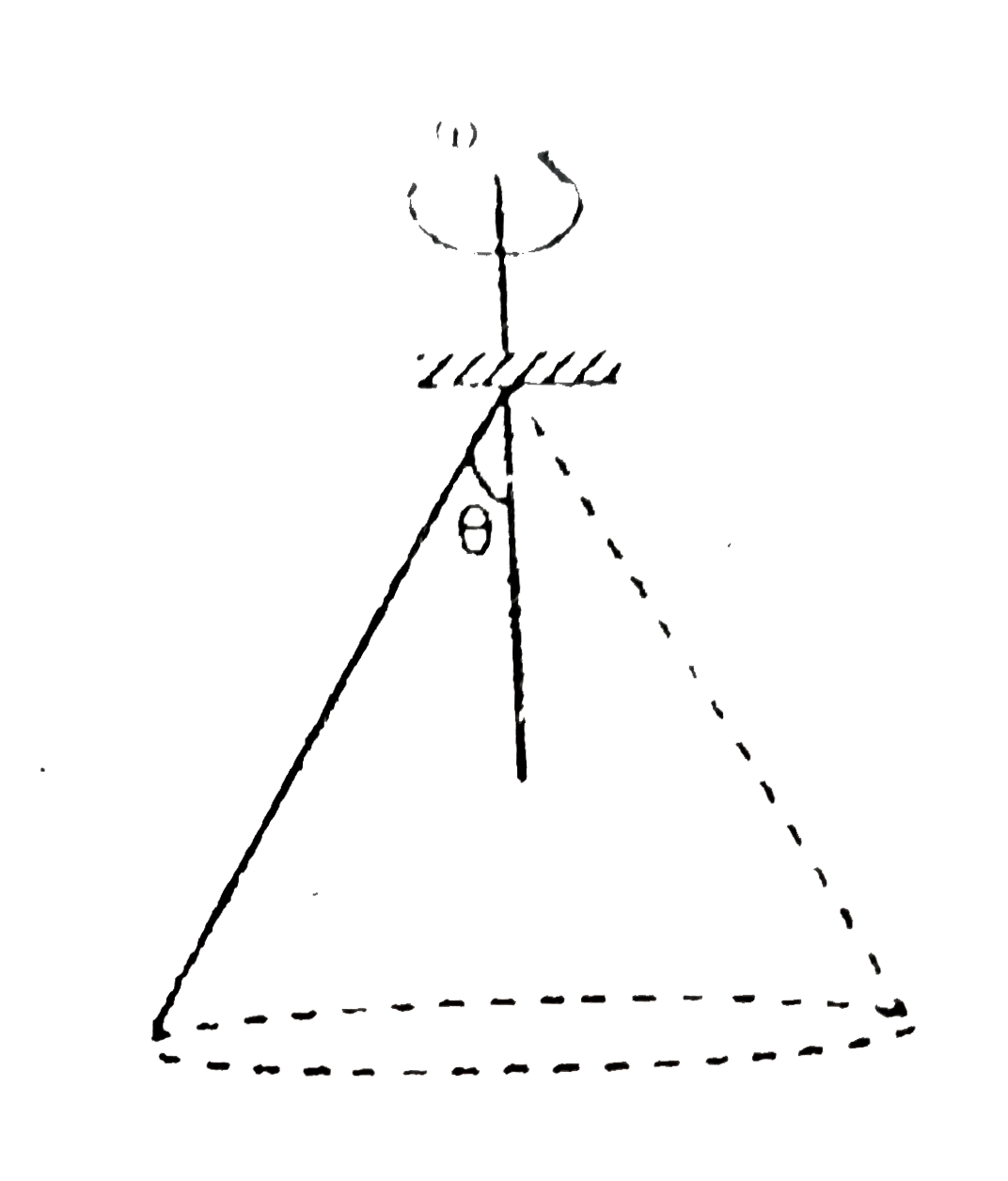
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.
View SolutionAssertion : Angular momentum of a planet is constant about any point
Reason : For acting on the planet is a central force.
View SolutionAssertion : In planetary motion angular momentum of planet about centre of sun remains constant. But linear momentum of system does not remain constant.
Reason : Net torque on planet any point is zero.
View SolutionSupose a planet is revolving around the sun in an elliptical path given by x2a2+y2b2=1
Find time period of revolution Angular momentum of the planet about the sun is L
 .
.
View Solution

