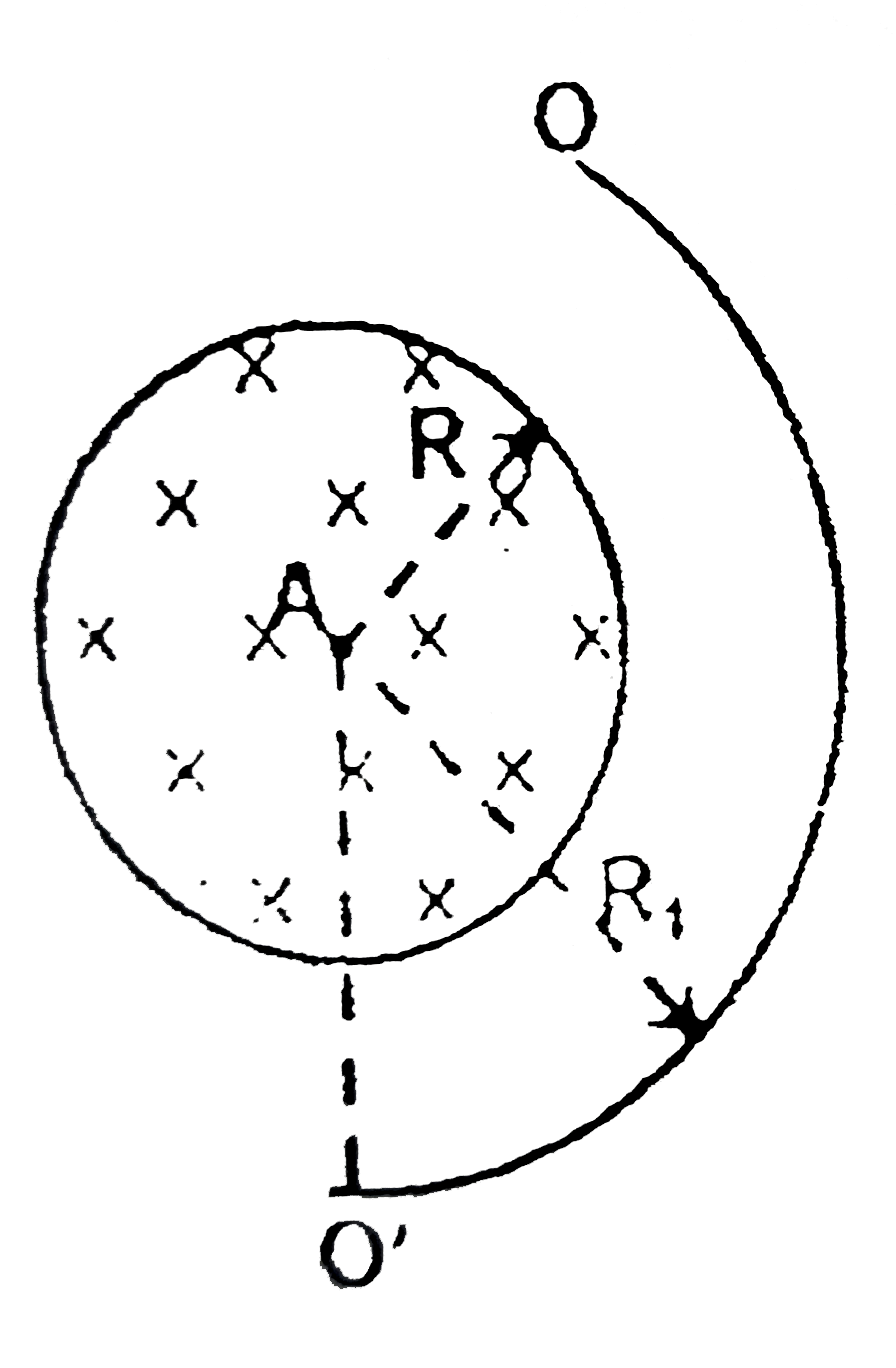
There is a uniform magnetic field $B$ in a circular region of radius $R$ as shown in Fig. 3.149 whose magnitude changes at the rate of $d B / d t$ . The emf circular concentric conducting arc of radius $R_{1}$ having an angle $θ$ as shown $(- O A O' = θ)$ is

$\frac{θ}{2 π} R_{1}^{2} \frac{d B}{d t}$

$\frac{θ}{2} R^{2} \frac{d B}{d t}$

$\frac{θ}{2 π} R^{2} \frac{d B}{d t}$

none of these

Video Solution

Text Solution

Verified by Experts

Required emf $= π R^{2} \frac{d B}{D t} \cdot \frac{θ}{2 π}$
$∴ E = \frac{R^{2}}{2 R_{1}} (\frac{d B}{d t})$
$e m f = \frac{θ}{2 π} \frac{R^{2}}{2 R_{1}} (\frac{d B}{D t}) 2 π R_{1} = \frac{θ}{2} R^{2} (\frac{d B}{d t})$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

The flux of electric field through the circular region of radius $r$ as shown in the figure is
View Solution
Magnetic field in cylindrical region of radius $R$ in inward direction is as shown in figure.

View Solution
A part of a long wire carrying a current $i$ is bent into a circle of radius $r$ as shown in figure. The net magnetic field at the centre $O$ of the circular loop is

View Solution
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View Solution
The magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate. $\frac{d B}{d t}$ . Then
View Solution
A particle of charge q and mass m is projected with a velocity $v_{0}$ toward a circular region having uniform magnetic field B perpendicular and into the plane of paper from point P as shown in Fig. 1.136. R is the radius and O is the center of the circular region. If the line OP makes an angle $θ$ with the direction of $v_{0}$ then the value of $v_{0}$ so that particle passes through O is

View Solution
In a very long solenoid of radius $R$ , if the magnetic field chabges at the rate of $d B / d t . A B = B C$
The induced emf for the trianglar circuit $A B C$ shown in Fig. 3.196 is

View Solution
a uniform magnetic field of induction $B$ fills a cylindrical volume of radius $R$ . A rod $A B$ of length $2 l$ is placed as shown in . If $B$ changing at the rate $d B / d t$ , the emf that is produced by the changing magnetic field and that acts between the ends of the rod is

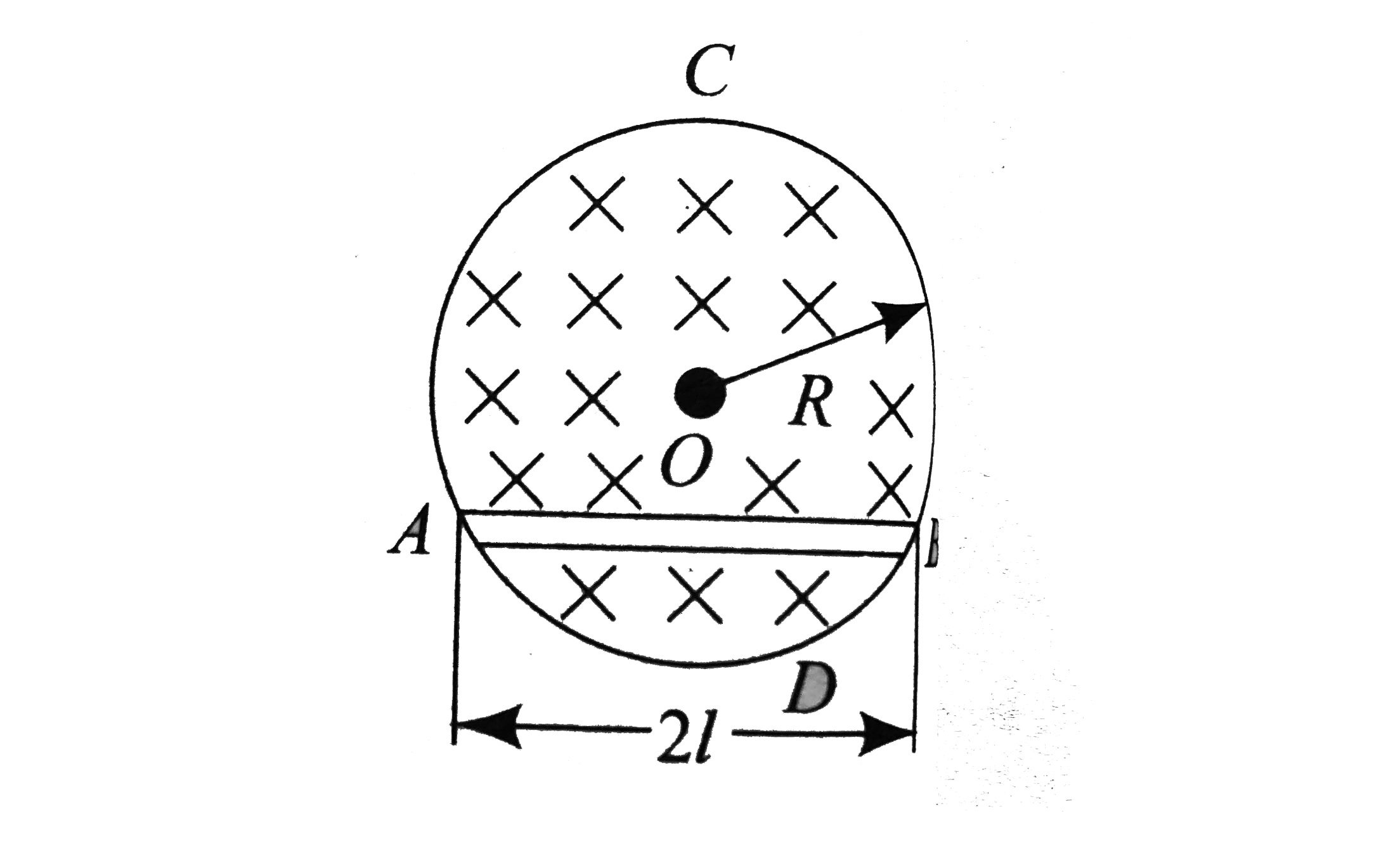
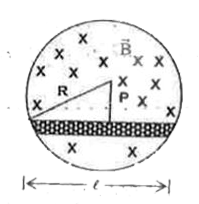
View Solution
A uniform magneitc field B fills a cylindrical volume of radius R, A metal rod of length l is placed as shown. If B is changing at the rate of dB/dt, the emf that is produced by the changing magnetic field is $ξ$ here p = $\sqrt{R^{2} - {(\frac{l}{2})}^{2}}$ . then

View Solution
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate $\frac{d B}{d t}$ . Loop 1 of radius R $>$ r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is

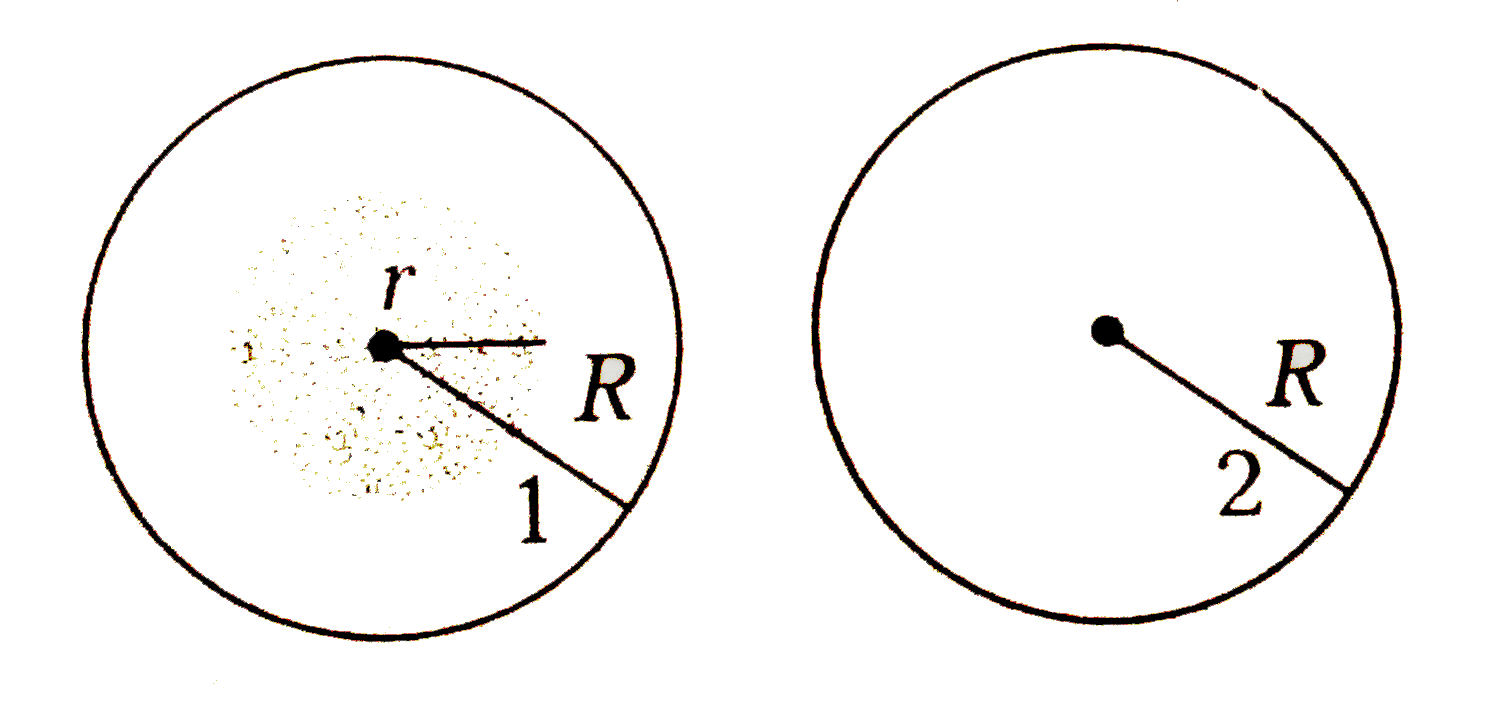
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
View Solution

There is a uniform magnetic field B in a circular region of radius R as shown in Fig. 3.149 whose magnitude changes at the rate of dB/dt. The emf circular concentric conducting arc of radius R1 having an angle θ as shown (−OAO'=θ) is

Required emf =πR2dBDt⋅θ2π ∴E=R22R1(dBdt) emf=θ2πR22R1(dBDt)2πR1=θ2R2(dBdt)

Similar Questions

Recommended Questions

There is a uniform magnetic field $B$ in a circular region of radius $R$ as shown in Fig. 3.149 whose magnitude changes at the rate of $d B / d t$ . The emf circular concentric conducting arc of radius $R_{1}$ having an angle $θ$ as shown $(- O A O' = θ)$ is

Required emf $= π R^{2} \frac{d B}{D t} \cdot \frac{θ}{2 π}$
$∴ E = \frac{R^{2}}{2 R_{1}} (\frac{d B}{d t})$
$e m f = \frac{θ}{2 π} \frac{R^{2}}{2 R_{1}} (\frac{d B}{D t}) 2 π R_{1} = \frac{θ}{2} R^{2} (\frac{d B}{d t})$