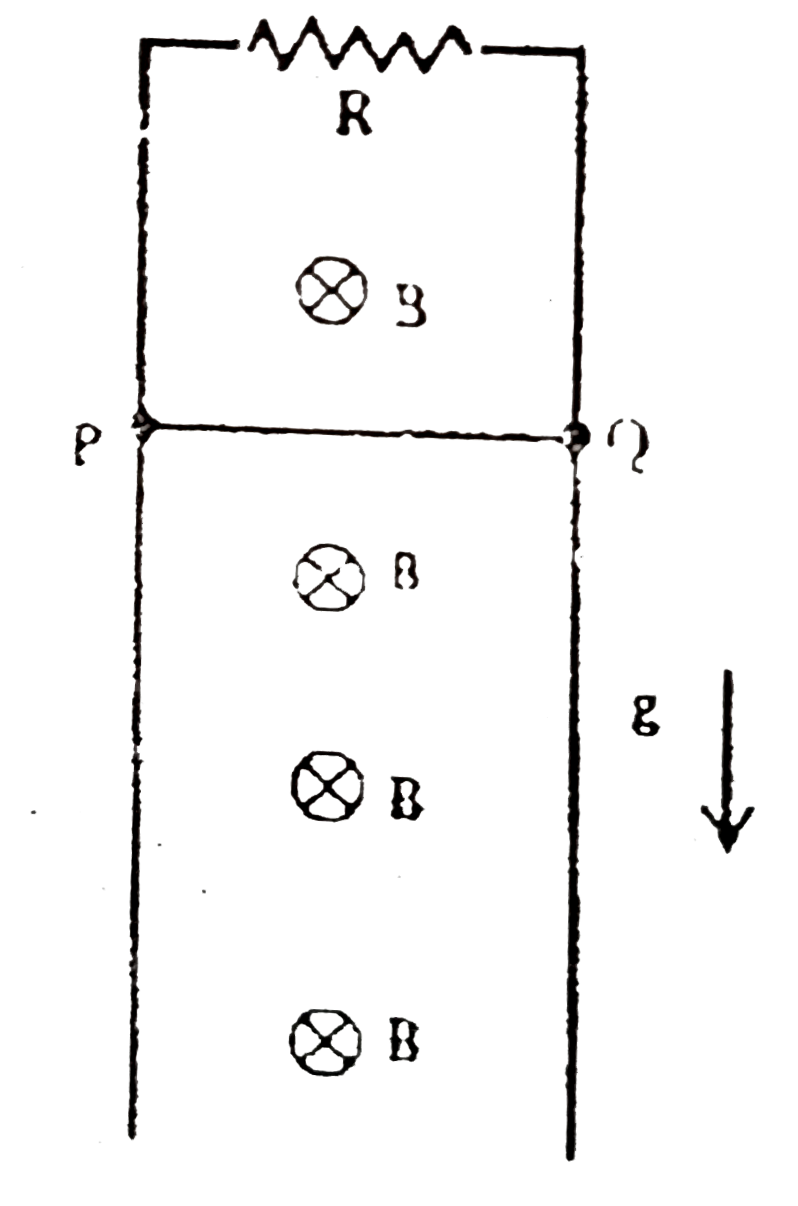
A rod PQ mass 'm' and length l can slide without friction on two vertical conducting semi infinite rails. It is given a velocity V0 downwards, so that it continues to move downward with the same speed V0 on its own at any later instant of time. Assuming g to be constant every where, the value of V0 is :-
mgR2B2L2
mgRB2L2
zero
Any value
B2V0L2R=mg
⇒V0=mgrB2L2
Similar Questions
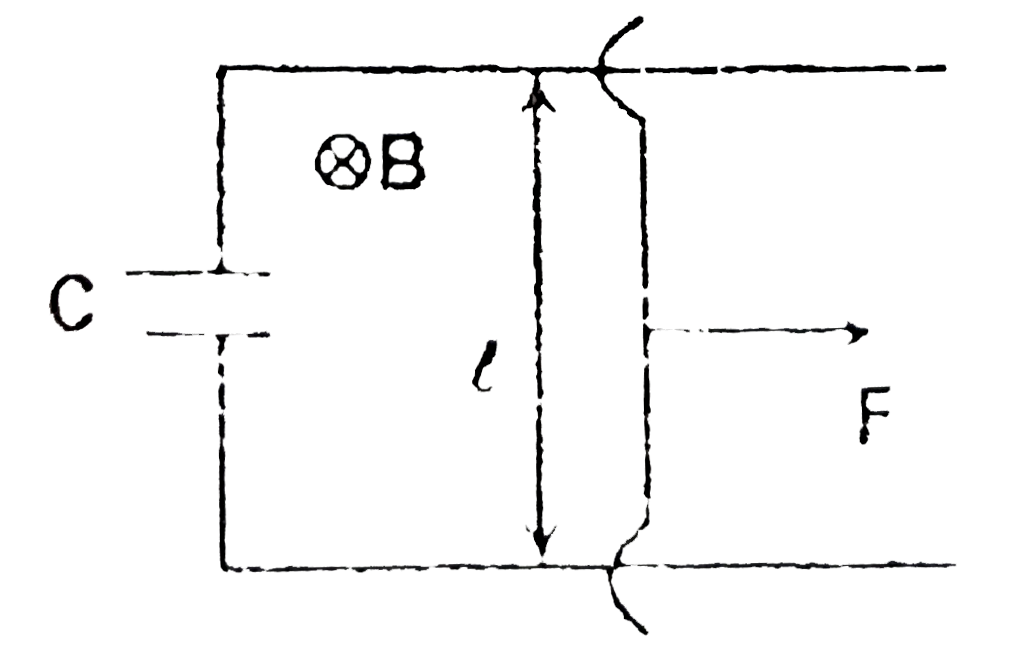
A conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
 View Solution
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. The whole system lies in amagnetic field B and a constant force F is applied to the rod . Then
 View Solution
View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of
 View Solution
View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of
 View Solution
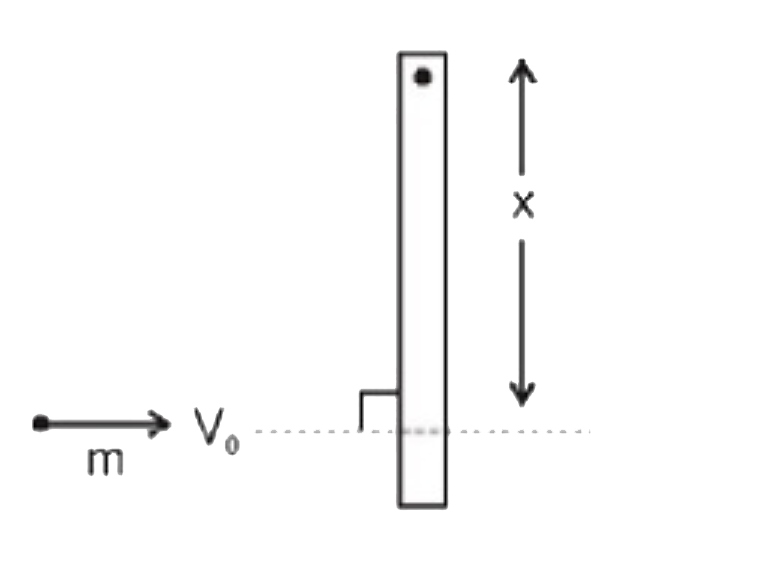
View SolutionA uniform rod of mass m and length L is hinged at one end and free to rotate in the horizontal plane. All the surface are smooth. A particle of same mass m collides with the rod with a speed V0. The coefficient of restitution for the collision is e=12. If hinge reaction during the collision is zero then the value of x is :
 View Solution
View SolutionA conducting rod of length L slides at a constant velocity V on two parallel conducting rails as shown in figure. The mechanical power required to pull the rod at constant velocity is
 View Solution
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
Velocity of particle at time is :View SolutionA rod of mass M and length L is falling vertically with speed v. Suddenly its one end gets stuck in a friciitonless hook. Find the angular velocity of the rod just after its end gets struck.
 View Solution
View SolutionA rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
As x is increased from 0 to l/2 , the angular speed ω.View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
After how much time, speed of particle decreases by 75%View Solution
