Two identical loudspeakers are placed on a line at distance 4m and 6m from a microphone lying on the line joining them. The output of each speaker at the microphone is 2mW. If the two speakers are connected in series and excited by the same oscillator and they vibrate in phase with each other, the resultant ouput of the microphone will be
(frequency of oscillator =660Hz and speed of sound =330m/s)
zero
2mW
4mW
8mW
To solve the problem, we need to find the resultant output of the microphone when two identical loudspeakers are connected in series and vibrate in phase. Here are the steps to arrive at the solution:
Step 1: Calculate the Wavelength (λ)
The wavelength can be calculated using the formula:
λ=vf
where:
- v is the speed of sound (330 m/s)
- f is the frequency of the oscillator (660 Hz)
Substituting the values:
λ=330m/s660Hz=0.5m
Step 2: Determine the Distances in Terms of Wavelength
Now, we need to express the distances of the loudspeakers from the microphone in terms of the wavelength:
- Distance from Speaker 1 to Microphone = 4 m
- Distance from Speaker 2 to Microphone = 6 m
Calculating the number of wavelengths:
- For Speaker 1:
4m0.5m=8λ
- For Speaker 2:
6m0.5m=12λ
Step 3: Determine the Phase Relationship
Since both speakers are vibrating in phase, and the distances correspond to whole numbers of wavelengths (8λ and 12λ), constructive interference occurs, leading to a maximum intensity at the microphone.
Step 4: Calculate the Intensities
The intensity I is related to the power output P by the formula:
I=PA
where A is the area over which the power is distributed. However, since we are given the output power directly, we can use the relationship that intensity is proportional to the square of the amplitude.
Given that the output of each speaker at the microphone is 2 mW, we can denote the amplitude from each speaker as A1 and A2. Since both speakers are identical:
P1=P2=2mW
Step 5: Calculate the Resultant Intensity
The resultant intensity Inet when both speakers are in phase is given by:
Inet=I1+I2
Since intensity is proportional to the square of the amplitude:
Inet=A21+A22
Given A1=A2 (both speakers are identical):
Inet=22+22=4+4=8mW
Final Result
Thus, the resultant output of the microphone when both speakers are connected in series and excited by the same oscillator is:
Resultant Output=8mW
The wavelength can be calculated using the formula:
λ=vf
where:
- v is the speed of sound (330 m/s)
- f is the frequency of the oscillator (660 Hz)
λ=330m/s660Hz=0.5m
Now, we need to express the distances of the loudspeakers from the microphone in terms of the wavelength:
- Distance from Speaker 1 to Microphone = 4 m
- Distance from Speaker 2 to Microphone = 6 m
- For Speaker 1:
4m0.5m=8λ
- For Speaker 2:
6m0.5m=12λ
Since both speakers are vibrating in phase, and the distances correspond to whole numbers of wavelengths (8λ and 12λ), constructive interference occurs, leading to a maximum intensity at the microphone.
The intensity I is related to the power output P by the formula:
I=PA
where A is the area over which the power is distributed. However, since we are given the output power directly, we can use the relationship that intensity is proportional to the square of the amplitude.
P1=P2=2mW
The resultant intensity Inet when both speakers are in phase is given by:
Inet=I1+I2
Since intensity is proportional to the square of the amplitude:
Inet=A21+A22
Given A1=A2 (both speakers are identical):
Inet=22+22=4+4=8mW
Thus, the resultant output of the microphone when both speakers are connected in series and excited by the same oscillator is:
Resultant Output=8mW
Similar Questions
Knowledge Check
Two identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2
Two springs are made to oscillate simple harmonically due to the same mass individually. The time periods obtained are T1 and T2. If both the springs are connected in series and then made to oscillate by the same mass, the resulting time period will be
View SolutionIf each of the two lines is perpendicular to the same line, what kind of lines are they to each other?
View SolutionThe distance between the two identical speakers shown in Fig. 14.3.3 are 4.00m. They are driven by the same osicllator. Initially a listner stays at L at a distance 8.0 m from the centre of the line connecting the two speakers. The listner then walks to the point A where AL=0.4m. The first minium is sound intensity in heard just the listener reaches the point A. Find the frequency of the oscillator. Speed of sound in air is 340 m/s.
View SolutionTwo loudspeakers are arranged facing each other at some distance. Will a person standing behind one of the loudspeakers clearly hear the sound of the other loudspeaker or the clarity will be seriously damaged because of the 'collision' of the two sounds in between ?
View SolutionTwo identical loudspeakers are driven in phase by a common oscillator at 800Hz and face each other at a distance of 1.25m. Locate the points along the line joining the two speakers where relative minimum of sound pressure amplitude would be expected. ( Use v=343m/s.)
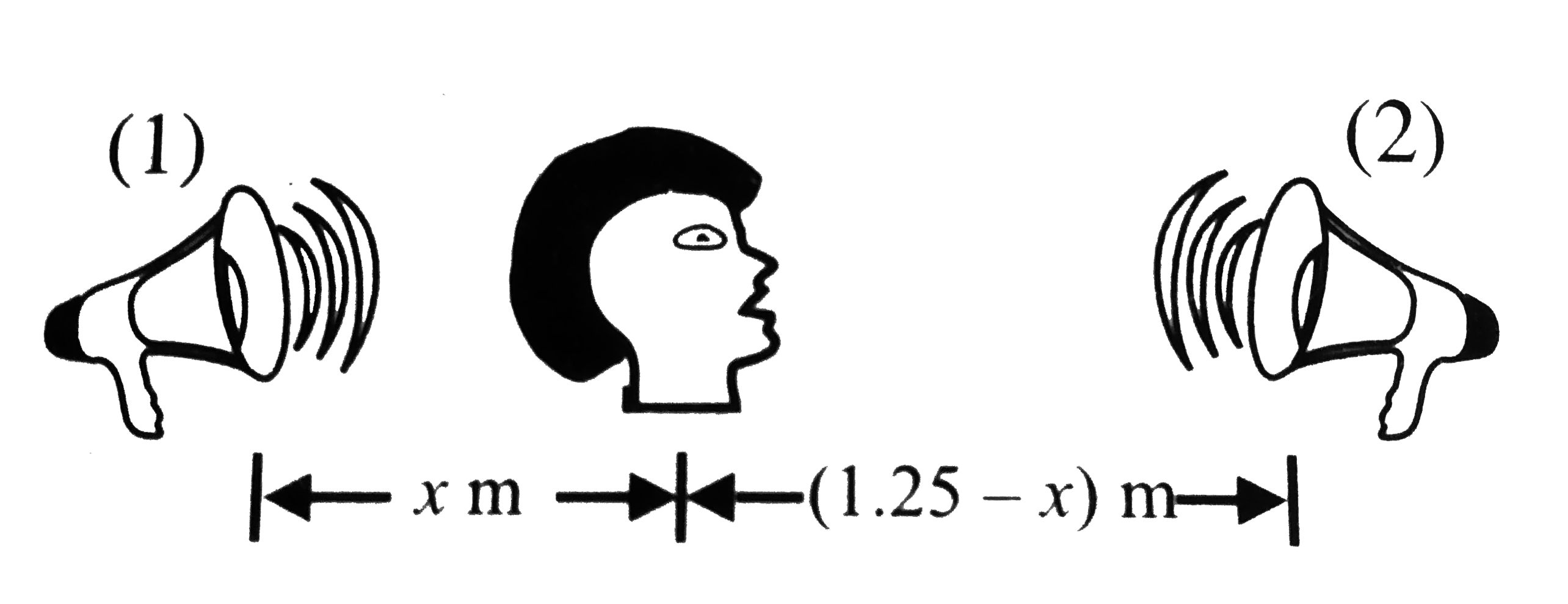
View SolutionWrite the energy conversions in
Microphone
View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
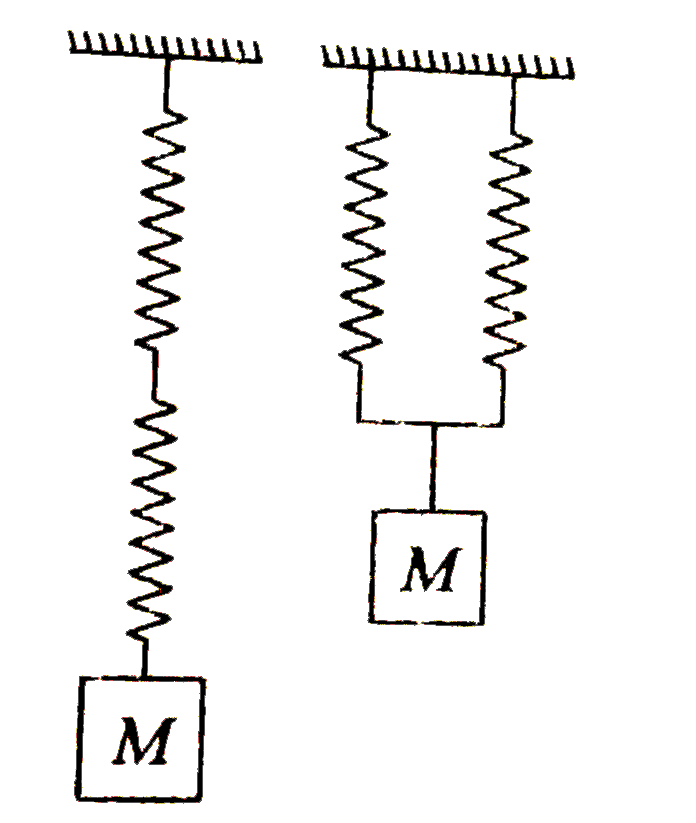
View Solution