A cavity is taken out from a uniform conducting sphere. Inside the cavity a dipole is placed as shown in the figure. Find the potential at point P (in Volt).
(q=10−8C, l=0.1mm, θ=30∘, d=10cm, R=12cm)
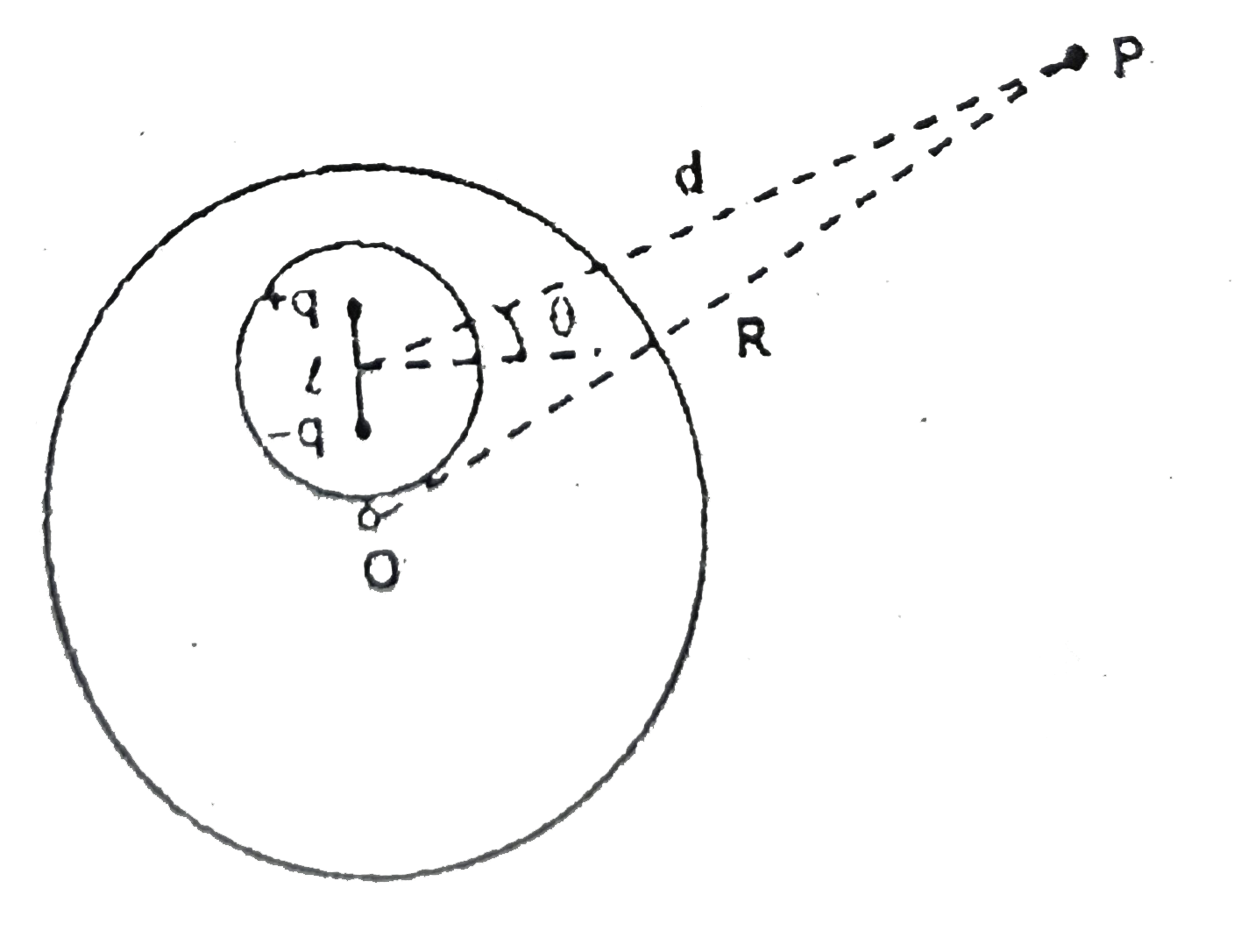
Charge on the outside surface of conducting sphere is zero so field and thus potential at any point outside the sphere is zero.
Similar Questions
The point charge is placed outside a spherical shell as shown i the figure. Find the electric potential (in kilo volt) on the surface of shell (Take: q=1μc and R=50cm)

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
 A1/2B7/9C3D7
A1/2B7/9C3D7
Inside a neutral hollow conducting sphere of radius X and centre C, a point charge q is placed as shown in the figure. Another point charge q1, is placed outside the sphere at distance d from centre. The net- electrostatic force on charge q placed at the centre is K=14πε0

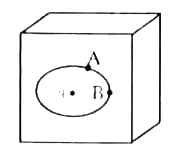
View SolutionAn ellipsoidal cavity is carved with in a perfect conductor. A positive charge q is placed at the centre of the cavity. The points A and B are on the cavity surface as shown in the figure then
(a) Electric field near A in the cavity = Electric field near B in the cavity
(b) Charge density at A= Charge density at B
(c ) Potential at A= Potential at B
(d) Total electric flux through the surface of the cavity is q/ε0.
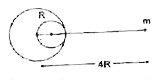
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
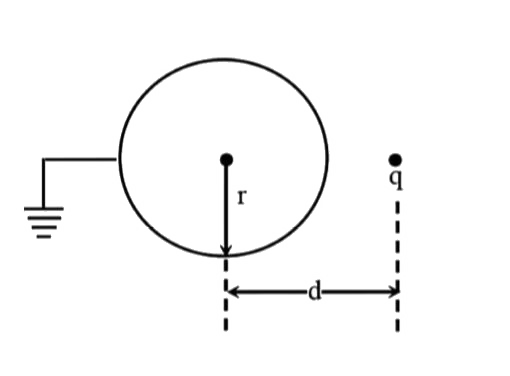
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
View SolutionPositive charge is uniformly distrubuted with volume charge density ρ of sphere of radius R. A spherical cavity is created in the sphere as shown in figure. This electric field intensity inside the cavity at point P is(where CP =R/5 , C0C = 2R/3 , radius of cavity is R/4, C0 & C are centre of sphere & cavity respectively)
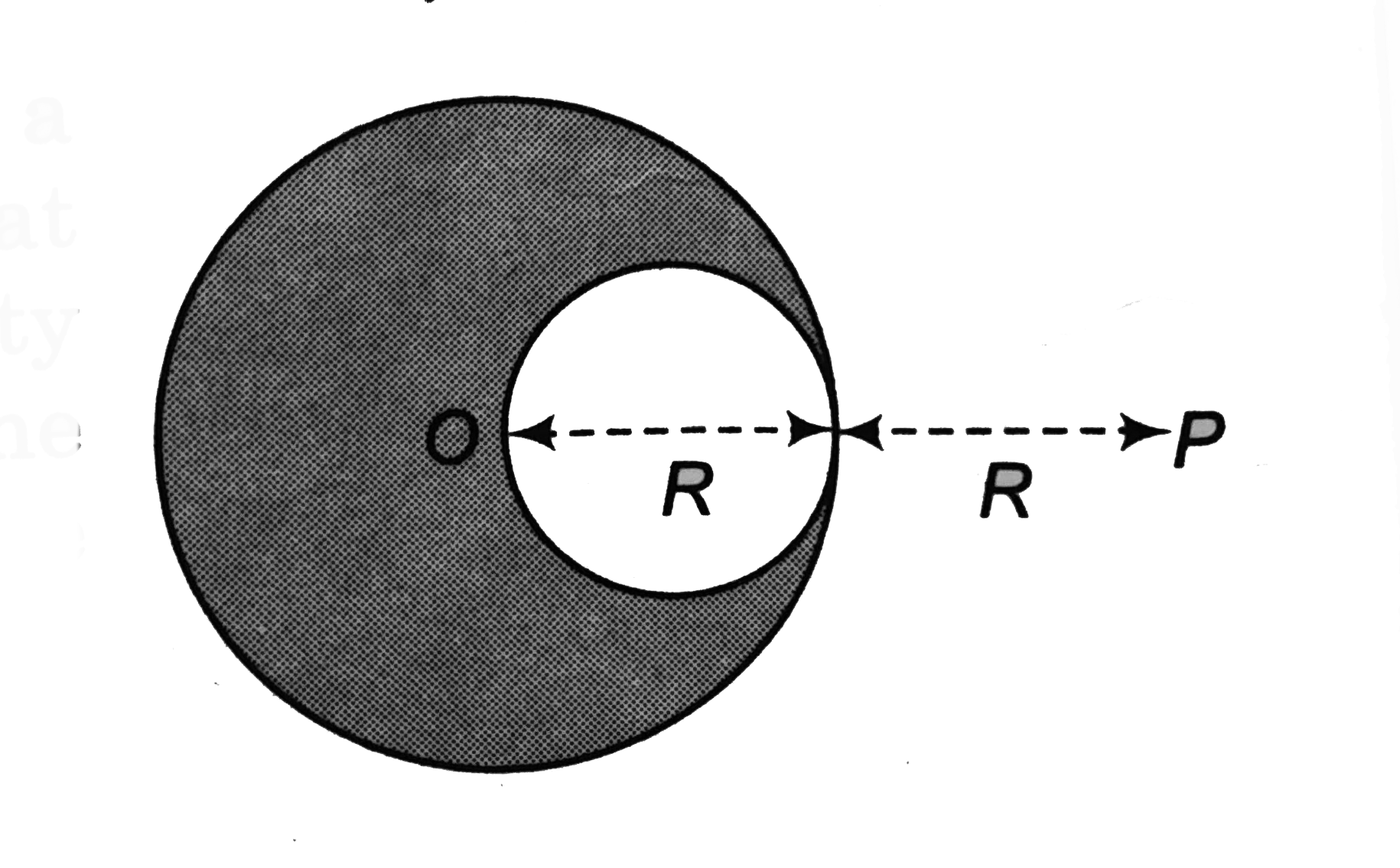
View SolutionThe point charge q is within the cavity of an electrically neutral conducting shell whose outer surface has spherical shape. Find the potential V at a point P lying outside the shell at distance r from the center O of the outer sphere.
 .
.
View SolutionA solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnetude) at point 'C' inside the cavity
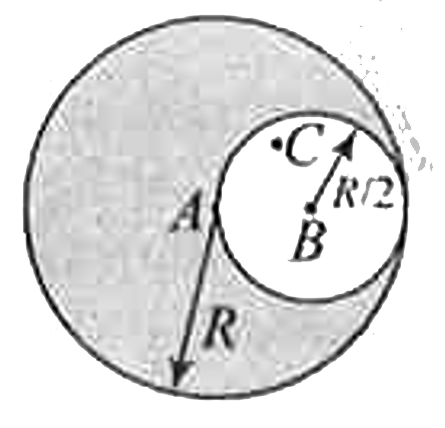
View Solution
