ΔABC is equilateral triangle of side a. P lies on AB such that A is midpoint of PB. If r1 is inradius of PAC and r2 is ex radius of PBC opposite to P, then r1+r2=
The correct Answer is:00000.50
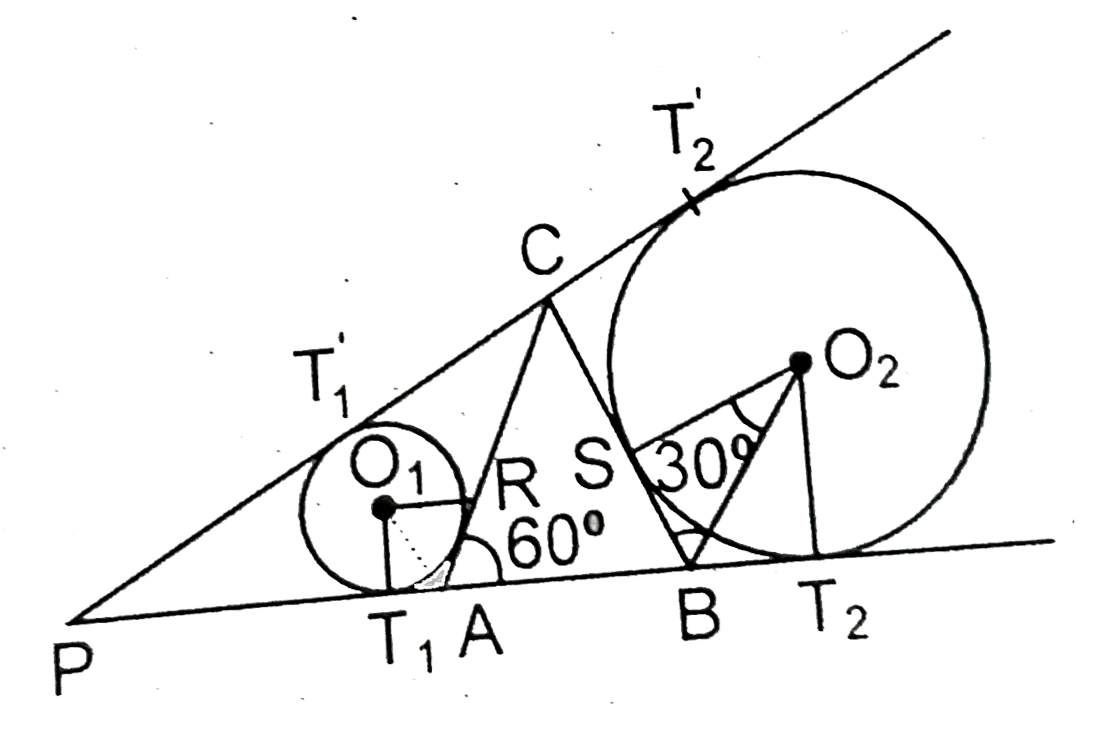
∠T1O1R=60∘ and ∠AO1R=0∘
similarly ∠BO2S=30∘
T1T2=T1A+AB+BT1=RA+RB+SB
=r1tan30∘+a+r2tan30∘=r1+r2√3+a
and T′1T′2=T′1C+T′2C=a−RA+a−BS=2a−r1+r2√3
Since common external tangents are equal T1T2=T′1T′2
⇒r1+r2=√3a2
Similar Questions
In the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
View SolutionLet ABC be an isosceles triangle with base BC. If r is the radius of the circle inscribsed in ΔABCandr1 is the radius of the circle ecribed opposite to the angle A, then the product r1r can be equal to (where R is the radius of the circumcircle of ΔABC)
View SolutionABC is an equilateral triangle of side 4cm. If R,randh are the circumradius, inradius, and altitude, respectively, then R+rh is equal to
View SolutionIn triangle ABC, let ∠C=π/2. If r is the inradius and R is circumradius of the triangle, then 2(r+R) is equal to
View SolutionIn an equilateral triangle with usual notations the value of 27r2Rr1r2r3is equal to
View SolutionABC is an equilateral triangle of side 4cm. If R,r,and,h are the circumradius, inradius, and altitude, respectively, then R+rh is equal to (a) 4 (b) 2 (c) 1 (d) 3
View SolutionIn a ΔABC,r1+r2+r3−r=
View SolutionIn a △ABC , if 2R + r =r1 , then
View SolutionIn an equilateral triangle show that the in-radius and the circum-radius are connected by r=R2.
View SolutionIn a triangle ABC if sides a = 13, b =14 and c = 15, then reciprocals of r1,r2,r3 are in the ratio
View Solution