Let $A B C$ be a triangle right-angled at $A a n d S$ be its circumcircle. Let $S_{1}$ be the circle touching the lines $A B$ and $A C$ and the circle $S$ internally. Further, let $S_{2}$ be the circle touching the lines $A B$ and $A C$ produced and the circle $S$ externally. If $r_{1}$ and $r_{2}$ are the radii of the circles $S_{1}$ and $S_{2}$ , respectively, show that $r_{1} r_{2} = 4$ area $(A B C) .$

A

$\frac{r_{1} r_{2}}{4}$

B

$\frac{r_{1} r_{2}}{8}$

C

$\frac{r_{1} r_{2}}{2}$

D

$r_{1} r_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Equation of $S = {(x - \frac{a}{2})}^{2} + {(y - \frac{b}{2})}^{2} = \frac{a^{2} + b^{2}}{4}$
$x^{2} + y^{2} - a x - b y = 0$
And circle with centre $(r, r)$ and radius $r$
Touches $A B$ and $A C$ its equation is
${(x - r)}^{2} + {(y - r)}^{2} = r^{2}$
$x^{2} + y^{2} - 2 x r - 2 y r + r^{2} = 0$
Both circle touches internally or externally
Using $\sqrt{{(r - \frac{a}{2})}^{2} + {(r - \frac{b}{2})}^{2}} = \sqrt{(\frac{a^{2}}{4} + \frac{b^{2}}{4})} \pm r$
$Δ A B C = \frac{r_{1} r_{2}}{4}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

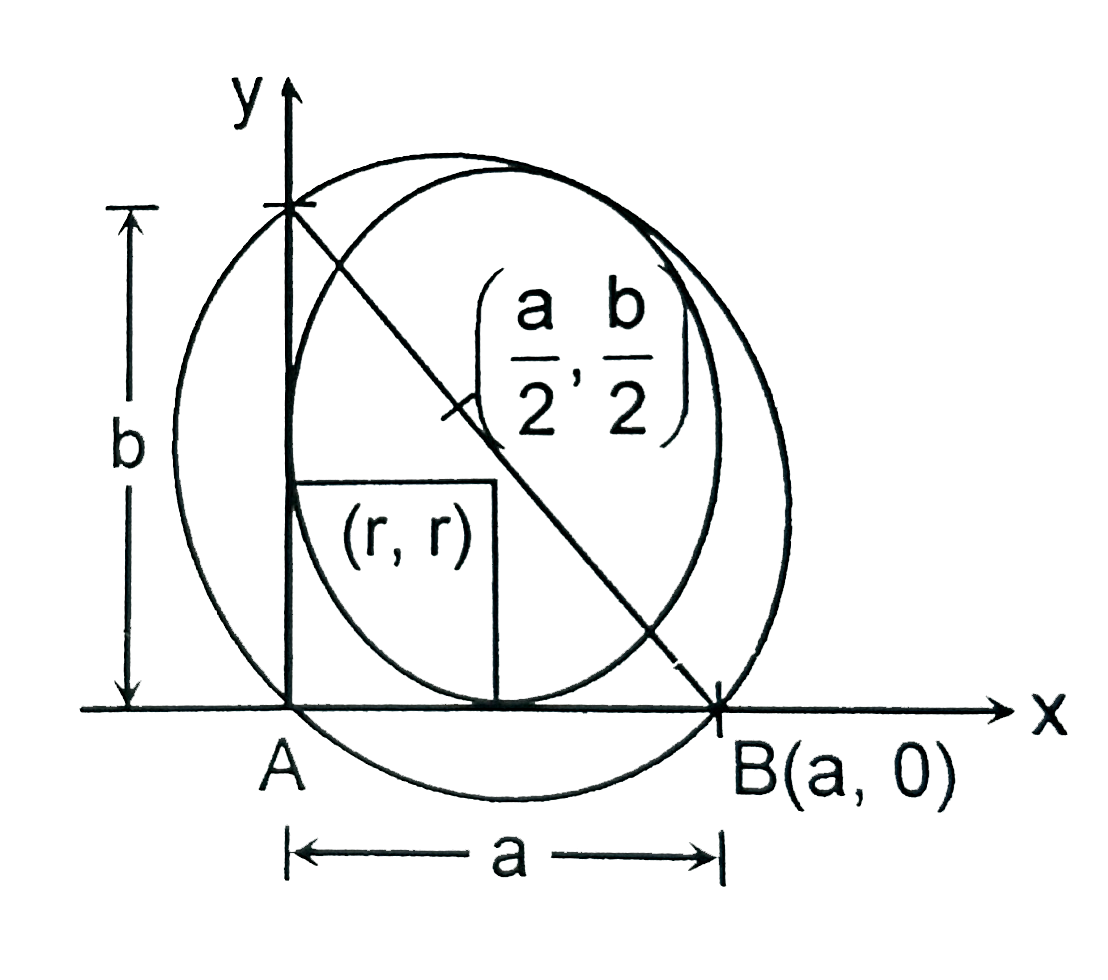
Similar Questions

Knowledge Check

Let S and S' be two (non - concentric circles with centres Aand B and radii $r_{1}, r_{2} and d$ be the distance between their centres , then one circle lies completely inside the other circle iff
A $d = r_{1} + r_{2}$
B $d = | r_{1} - r_{2} |$
C $d = | r_{2} - r_{1} |$
D $d < | r_{1} - r_{2} |$

Recommended Questions

Home
Ask Doubt
Profile