A sugar exist in two isomeric form α−D & β−D with specific rotation of 110∘ and 30∘ respectively. When α−D form of the suar is dissolved in water exhibits mutarotation till the equilibrium value of 90∘ is attained. The equilibrium constant of mutarotation of β−D form [Assuming only α and β form in solution] is equal to:
The correct Answer is:00003.33
To solve the problem, we need to determine the equilibrium constant for the mutarotation of the sugar from its alpha-D form to its beta-D form. Here are the steps to arrive at the solution:
1. Understanding the Given Information:
- Specific rotation of α-D: (α)α=110∘
- Specific rotation of β-D: (α)β=30∘
- Equilibrium specific rotation after mutarotation: (α)eq=90∘
2. Setting Up the Equilibrium:
- Let x be the fraction of the α-D form at equilibrium.
- Then, the fraction of the β-D form at equilibrium will be 1−x.
3. Using the Specific Rotation Formula:
- The specific rotation at equilibrium can be expressed as:
(α)eq=x⋅(α)α+(1−x)⋅(α)β
- Substituting the known values:
90=x⋅110+(1−x)⋅30
4. Solving for x:
- Expanding the equation:
90=110x+30−30x
- Simplifying:
90=80x+30
- Rearranging gives:
80x=90−30=60
- Therefore:
x=6080=34
5. Finding the Equilibrium Constant Kc:
- The equilibrium constant for the mutarotation can be defined as:
Kc=(β)(α)=1−xx
- Substituting x=34:
Kc=1−3434=1434=13
6. Final Answer:
- The equilibrium constant Kc for the mutarotation of the β-D form is:
Kc=13≈0.33
- Specific rotation of α-D: (α)α=110∘
- Specific rotation of β-D: (α)β=30∘
- Equilibrium specific rotation after mutarotation: (α)eq=90∘
- Let x be the fraction of the α-D form at equilibrium.
- Then, the fraction of the β-D form at equilibrium will be 1−x.
- The specific rotation at equilibrium can be expressed as:
(α)eq=x⋅(α)α+(1−x)⋅(α)β
- Substituting the known values:
90=x⋅110+(1−x)⋅30
- Expanding the equation:
90=110x+30−30x
- Simplifying:
90=80x+30
- Rearranging gives:
80x=90−30=60
- Therefore:
x=6080=34
- The equilibrium constant for the mutarotation can be defined as:
Kc=(β)(α)=1−xx
- Substituting x=34:
Kc=1−3434=1434=13
- The equilibrium constant Kc for the mutarotation of the β-D form is:
Kc=13≈0.33
Similar Questions
When either form of D-Glucose is dissolved In water, the solution gradually changes its optical rotation and finally attains a constant optical rotation of +52∘.

Which form of D-GIucose is more stable?View SolutionWhen α−D glucose is dissolved in water, it undergoes a partial converion to β−D glucose to exhibit mutarotation. This conversion stops when 63.6% of glucose is in β form. Assuming that equilibrium has been attained, calculate Kc for mutarotation.
View Solution
Knowledge Check
- Question 1 - Select One
1.1 moles of A are mixed with 2.2 moles of B and the mixture is kept in a one litre flask till the equilibrium
A+2B⇔2C+D
is reached. At equilibrium, 0.2 moles of C are formed. The equilibrium constant of the reaction isA0.001B0.002C0.0033D0.004 - Question 2 - Select One
D (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
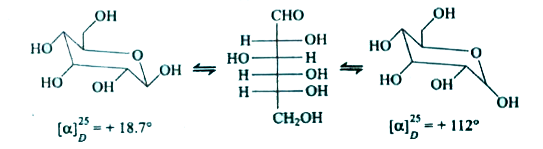
What percentage of β-D-(+) glucopyranose found at equilibrium in the aqueous solution?A50%B≈100%C38%D64%
When either form of D-Glucose is dissolved In water, the solution gradually changes its optical rotation and finally attains a constant optical rotation of +52∘.

What is the percentage of open chain D-Glucose in solution?View SolutionWhen either form of D-Glucose is dissolved In water, the solution gradually changes its optical rotation and finally attains a constant optical rotation of +52∘.

Which of the following statements, is true?View SolutionWhen 4mol of A is mixed with 4mol of B,2mol of C and D are formed at equilibrium, according to the reaction
A+B⇔C+D
the equilibrium constant isView Solution4 moles of A are mixed with 4 moles of B, when 2 moles of C are formed at equilibrium according to the reaction A+B⇔C+D.
The value of equilibrium constant isView SolutionOne mole of A reacts with one mole of B to form 0.1 mole of C and 0.1 mole of D . What will be the value of the equilibrium constant ?
A+B⇒C+DView Solution1.1 mole of A mixed with 2.2 mole of B and then the mixture is then kept in one litre flask till the equilibrium is attained A+2B⇌2C+D . At the equilibrium 0.2 mole of C is formed, then the value of Kc will be:
View Solution
