A uniform conducting ring of mass m=2kg, radius r=2m and resistance 8Ω is kept on smooth, horizontal surface. A time varying magnetic field →B=(ˆi+t2ˆj) Tesla is present in the region, where t is time in second and take vertical as y-axis. (Take π2=10). Then
Time when ring starts toppling is 1/2 sec
Time when ring starts toppling is 3/4 sec
Heat generated through the ring till the instant when the ring start toppling is 40/3 Joule.
Heat generated through the ring till the instant when the ring start toppling is 80/3 Joule
The correct Answer is:A, D
To solve the problem, we need to determine the time when the conducting ring starts to topple due to the induced current in the presence of a time-varying magnetic field. We will analyze the torques acting on the ring due to its weight and the magnetic field.
1. Identify the Forces and Torques:
- The ring has a mass m=2kg.
- The weight of the ring Fw=mg=2×10=20N acts downwards.
- The torque due to the weight τw is given by:
τw=r×Fw=2m×20N=40N m
2. Calculate the Magnetic Flux:
- The magnetic field is given by →B=^i+t2^j.
- The area A of the ring is A=πr2=π(22)=4πm2.
- The magnetic flux Φ through the ring is:
Φ=∫→B⋅d→A=∫(1^i+t2^j)⋅(0^i+1^j)dA=4πt2
3. Calculate the Induced EMF:
- The induced EMF E is given by:
E=−dΦdt=−ddt(4πt2)=−8πt
4. Calculate the Induced Current:
- The resistance R of the ring is 8Ω.
- The induced current I is given by:
I=ER=−8πt8=−πt
5. Calculate the Force due to the Magnetic Field:
- The force FB on the ring due to the magnetic field is given by:
FB=IA×→B=(−πt)(4π)^j×(^i+t2^j)=−4π2t^k
6. Calculate the Torque due to the Magnetic Field:
- The torque τB due to the magnetic field is:
τB=r×FB=2^r×(−4π2t^k)=8π2tN m
7. Set the Torques Equal to Find the Time:
- The ring will start to topple when the torque due to the magnetic field equals the torque due to the weight:
τB=τw⟹8π2t=40
- Substituting π2=10:
80t=40⟹t=12s
Final Answer:
The time when the ring starts to topple is t=12s.
- The ring has a mass m=2kg.
- The weight of the ring Fw=mg=2×10=20N acts downwards.
- The torque due to the weight τw is given by:
τw=r×Fw=2m×20N=40N m
- The magnetic field is given by →B=^i+t2^j.
- The area A of the ring is A=πr2=π(22)=4πm2.
- The magnetic flux Φ through the ring is:
Φ=∫→B⋅d→A=∫(1^i+t2^j)⋅(0^i+1^j)dA=4πt2
- The induced EMF E is given by:
E=−dΦdt=−ddt(4πt2)=−8πt
- The resistance R of the ring is 8Ω.
- The induced current I is given by:
I=ER=−8πt8=−πt
- The force FB on the ring due to the magnetic field is given by:
FB=IA×→B=(−πt)(4π)^j×(^i+t2^j)=−4π2t^k
- The torque τB due to the magnetic field is:
τB=r×FB=2^r×(−4π2t^k)=8π2tN m
- The ring will start to topple when the torque due to the magnetic field equals the torque due to the weight:
τB=τw⟹8π2t=40
- Substituting π2=10:
80t=40⟹t=12s
The time when the ring starts to topple is t=12s.
Similar Questions
A uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
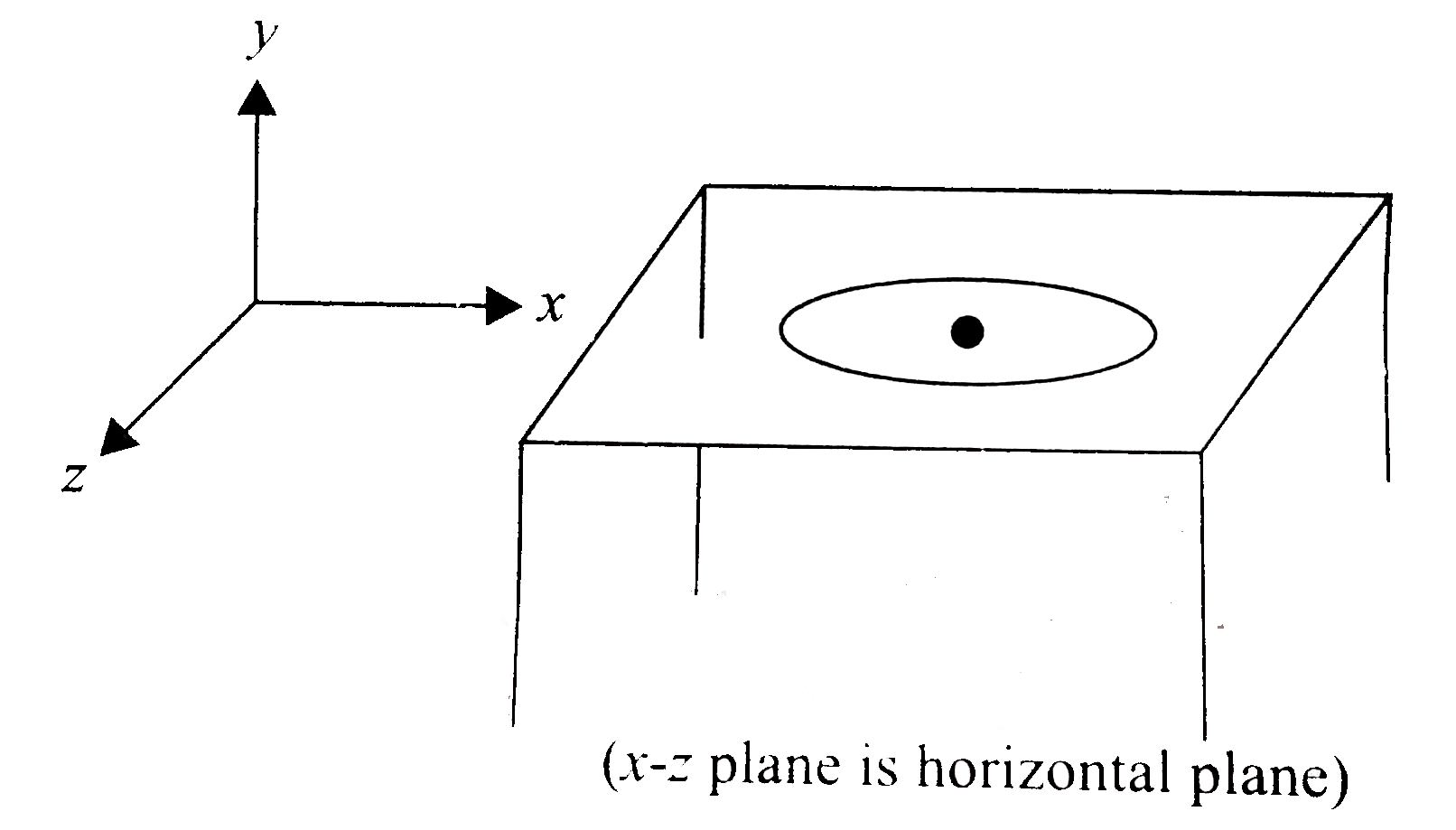
Time (in second) at which ring start toppling is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Time (in second) at which ring start toppling is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
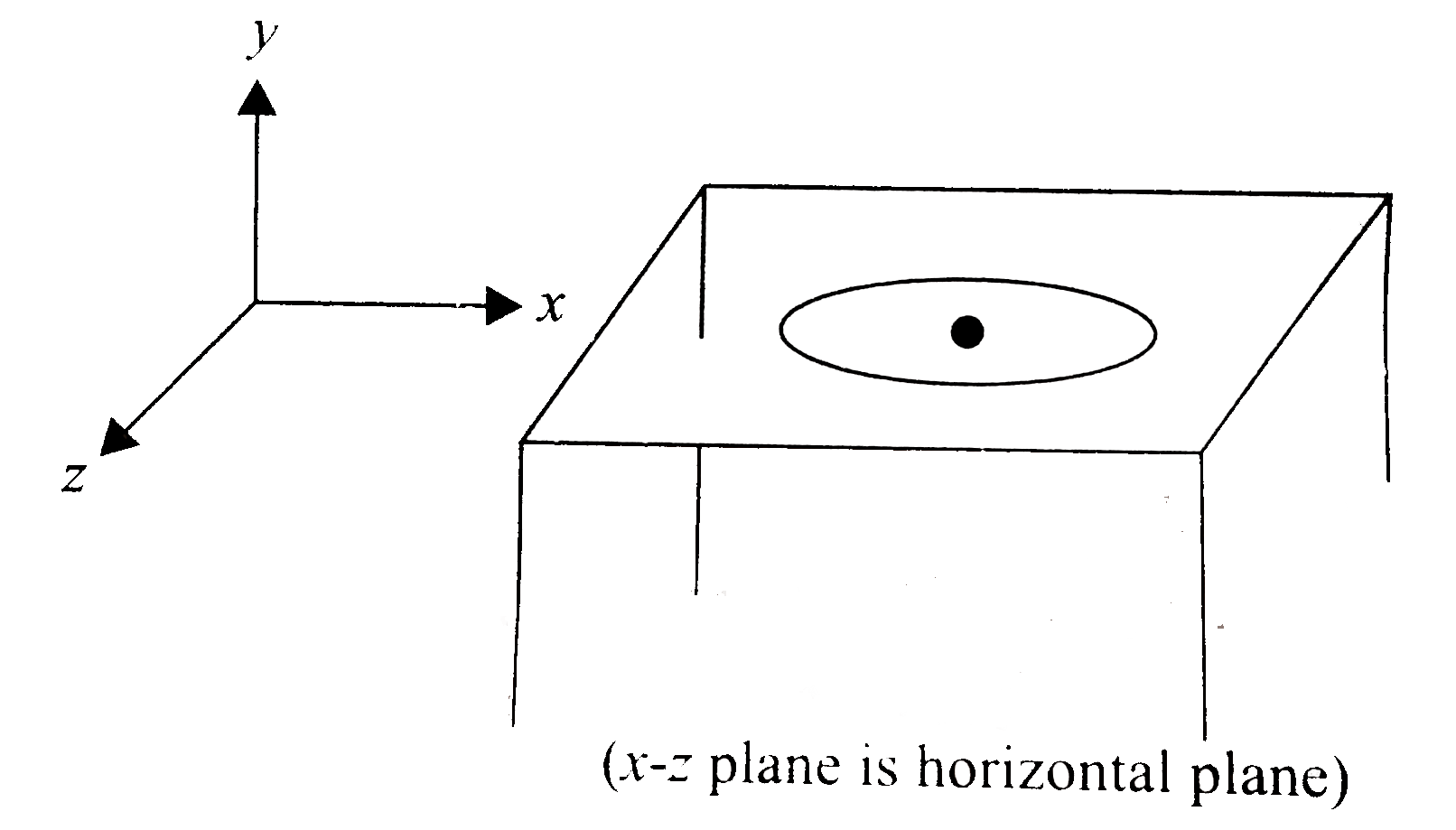
Net Induced EMF (in Volt) on conducting ring as function of time is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
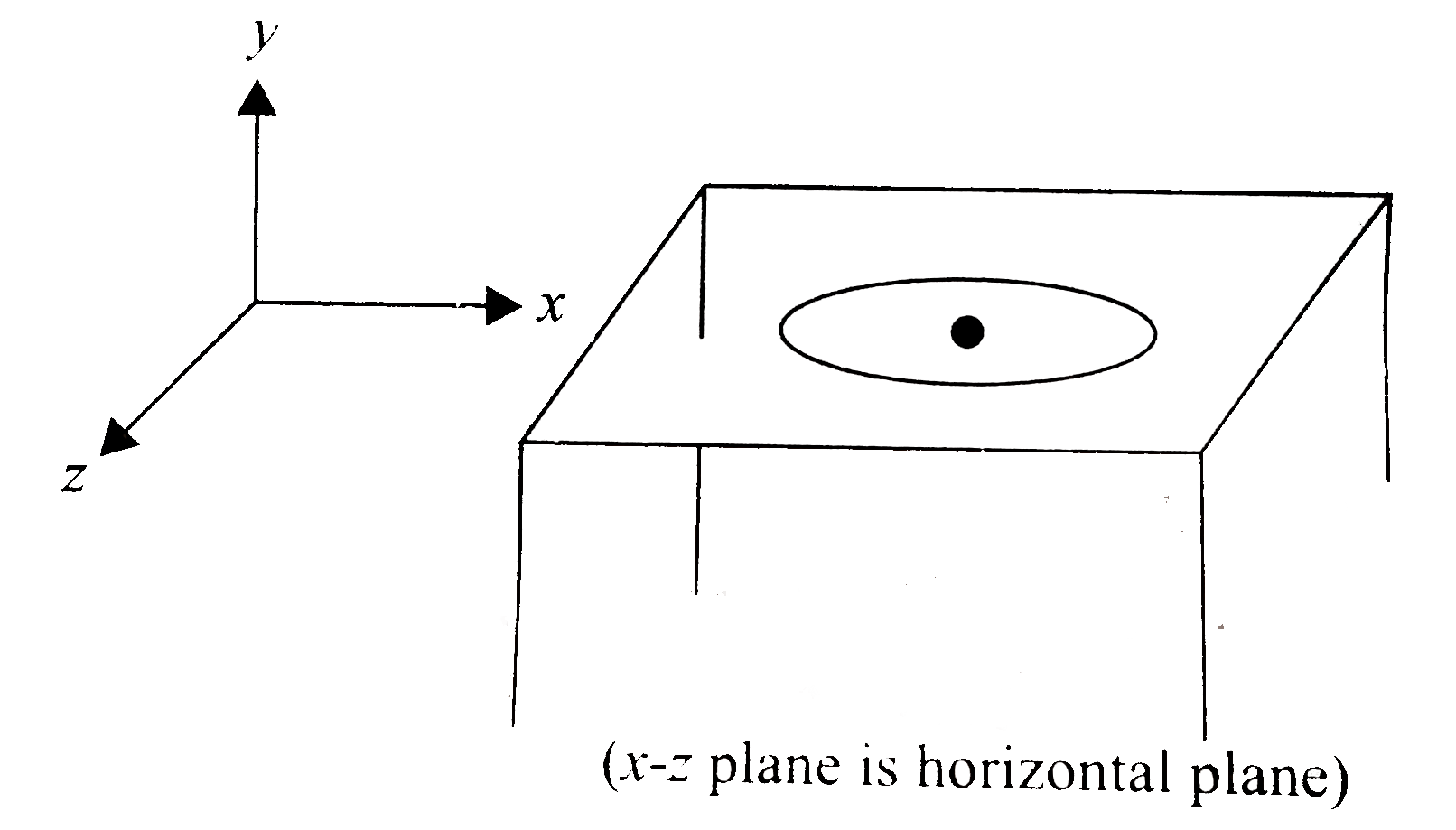
Heat generated (in kJ) through the ring till the instant when ring start toppling is
View SolutionA conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
View SolutionA conducting ring of mass 2kg, radius 0.5m carries a current of 4A. It is placed on a smooth horizontal surface. When a horizontal magnetic field of 10 T parallel to the diameter of the ring is applied, the initial acceleration is (in rad/sec2)

View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA circular conducting coil of radius r0, having resistance R is placed in a time varying transverse uniform magnetic field B=4t2 as shown in the figure. The current in the coil at time t = 2 s is (consider all quantities are in Si units)
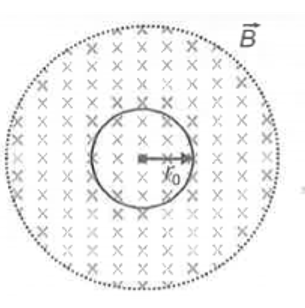
View Solution

