A disc is free ot rotate about an axis passing through its centre and perpendicular to its plane. The moment of inertia of the disc about its rotation axis is I. A light ribbon is tightly wrapped over it in multiple layers. The end of the ribbon is pulled of the ribboned disc be R at any time and thickness of the ribbon ve d(<<R). Then the force (F) required to pull the ribbon as a funcation of radius R is.
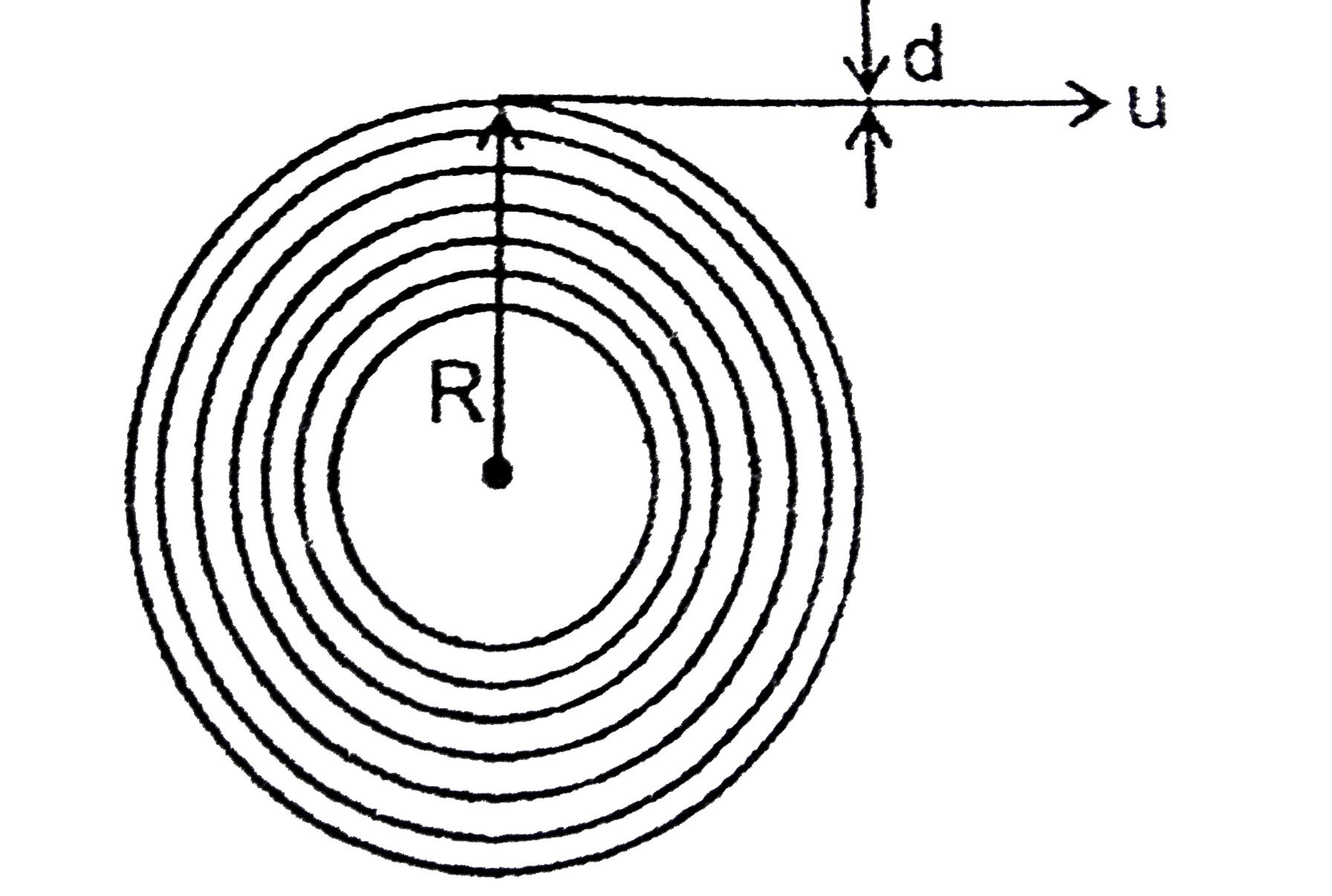
Angular acceleration of the disc at any insant is proportional to 1R3, where R is radius of the ribboned disc
Angular acceleration o the disc at any instant is proportional to 1R2 where R is the radius of the ribboned disc.
Force required to pull the ribbon at constant speed u is F=Iu2d2πR4
Force required to pull the ribbon at constant speed u is F=Iu2dπR4
The correct Answer is:A, C
ωR=u=constant
ωdRdt+Rdωdt=0
∴dωdt=−ωRdRdt
In time dt radius decreases by dR
−2πRdR=uddt
∴dRdt=−ud2πR
dωdt=α=ωRud2πR
α=u2d2πR3
τ=Iu2d2πR3
∴F=Iu2d2πR4
Similar Questions
A disc is free to rotate about an axis passing through its centre and perpendicular to its plane. The moment of inertia of the disc about its rotation axis is I. A light ribbon is tightly wrapped over it in multiple layers. The end of the ribbon is pulled out at a constant speed of u. Let the radius of the ribboned disc be R at any time and thickness of the ribbon be d(<<R). Find the force (F) required to pull the ribbon as a function of radius R.

View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionDerive an expression for the MI. of a disc,
(i) about an axis passing through its centre and perpendicular to its plane. (ii) about its diameter.
View SolutionA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
View SolutionA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionA nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity ω . The magnt moment of this disc is .
View SolutionThe rotational inertia of a disc about its geometrical axis does not depend upon its
View Solution
