A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
What is the magnitude of normal component of final velocity of the smaller disc'?
The correct Answer is:A, C, D
To solve the problem step by step, we need to analyze the elastic collision between the two discs.
Step 1: Understand the System
We have two circular discs:
- Disc 1 (heavier disc): Mass = 2m, Radius = 3r (at rest)
- Disc 2 (smaller disc): Mass = m, Radius = 2r (moving with velocity u)
The collision is elastic, which means both momentum and kinetic energy are conserved.
Step 2: Determine the Normal Component of Velocity
The normal component of velocity is the component of the velocity that is perpendicular to the surface at the point of impact.
Step 3: Set Up the Equations for Conservation of Momentum
For elastic collisions, the conservation of momentum can be expressed as:
m1u1+m2u2=m1v1+m2v2
Where:
- m1=2m (mass of the heavier disc)
- u1=0 (initial velocity of the heavier disc)
- m2=m (mass of the smaller disc)
- u2=u (initial velocity of the smaller disc)
- v1 = final velocity of the heavier disc
- v2 = final velocity of the smaller disc
Substituting the values, we get:
0+mu=2mv1+mv2
This simplifies to:
u=2v1+v2(Equation 1)
Step 4: Set Up the Equations for Conservation of Kinetic Energy
The conservation of kinetic energy for elastic collisions can be expressed as:
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the values, we get:
0+12mu2=12(2m)v21+12mv22
This simplifies to:
u2=2v21+v22(Equation 2)
Step 5: Solve the Equations Simultaneously
From Equation 1, we can express v1 in terms of v2:
v1=u−v22
Substituting this into Equation 2:
u2=2(u−v22)2+v22
Expanding and simplifying gives us a quadratic equation in terms of v2.
Step 6: Calculate the Final Velocities
After solving the quadratic equation, we can find the values of v1 and v2.
Step 7: Find the Normal Component of the Final Velocity of the Smaller Disc
The normal component of the final velocity of the smaller disc is simply v2.
Final Answer
The magnitude of the normal component of the final velocity of the smaller disc is:
v2=u5
We have two circular discs:
- Disc 1 (heavier disc): Mass = 2m, Radius = 3r (at rest)
- Disc 2 (smaller disc): Mass = m, Radius = 2r (moving with velocity u)
The normal component of velocity is the component of the velocity that is perpendicular to the surface at the point of impact.
For elastic collisions, the conservation of momentum can be expressed as:
m1u1+m2u2=m1v1+m2v2
Where:
- m1=2m (mass of the heavier disc)
- u1=0 (initial velocity of the heavier disc)
- m2=m (mass of the smaller disc)
- u2=u (initial velocity of the smaller disc)
- v1 = final velocity of the heavier disc
- v2 = final velocity of the smaller disc
0+mu=2mv1+mv2
This simplifies to:
u=2v1+v2(Equation 1)
The conservation of kinetic energy for elastic collisions can be expressed as:
12m1u21+12m2u22=12m1v21+12m2v22
Substituting the values, we get:
0+12mu2=12(2m)v21+12mv22
This simplifies to:
u2=2v21+v22(Equation 2)
From Equation 1, we can express v1 in terms of v2:
v1=u−v22
u2=2(u−v22)2+v22
Expanding and simplifying gives us a quadratic equation in terms of v2.
After solving the quadratic equation, we can find the values of v1 and v2.
The normal component of the final velocity of the smaller disc is simply v2.
The magnitude of the normal component of the final velocity of the smaller disc is:
v2=u5
Similar Questions
A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
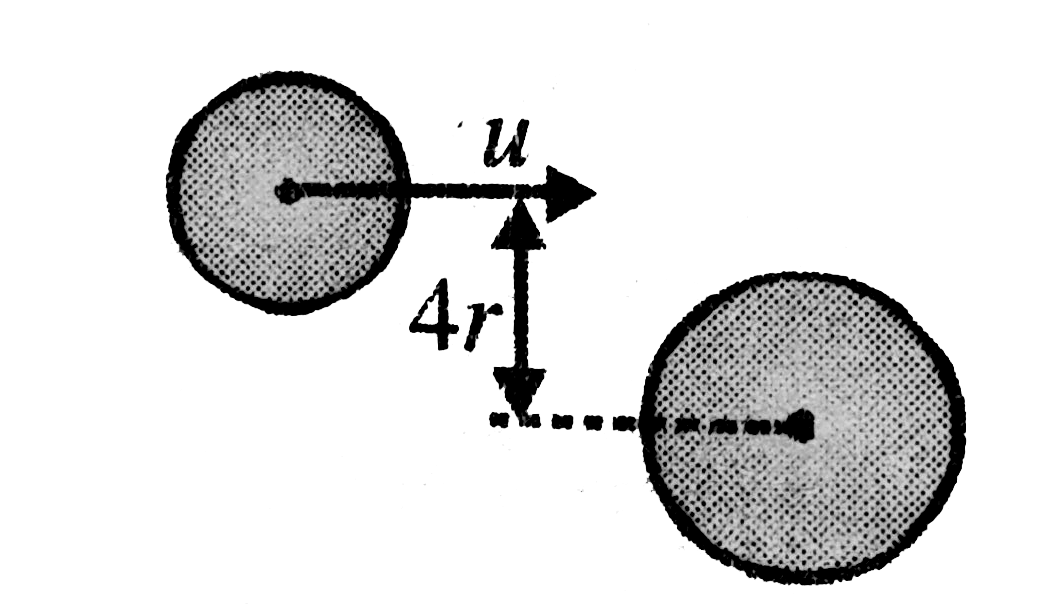
What is the tangential component of final velocity of the smaller disc?
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
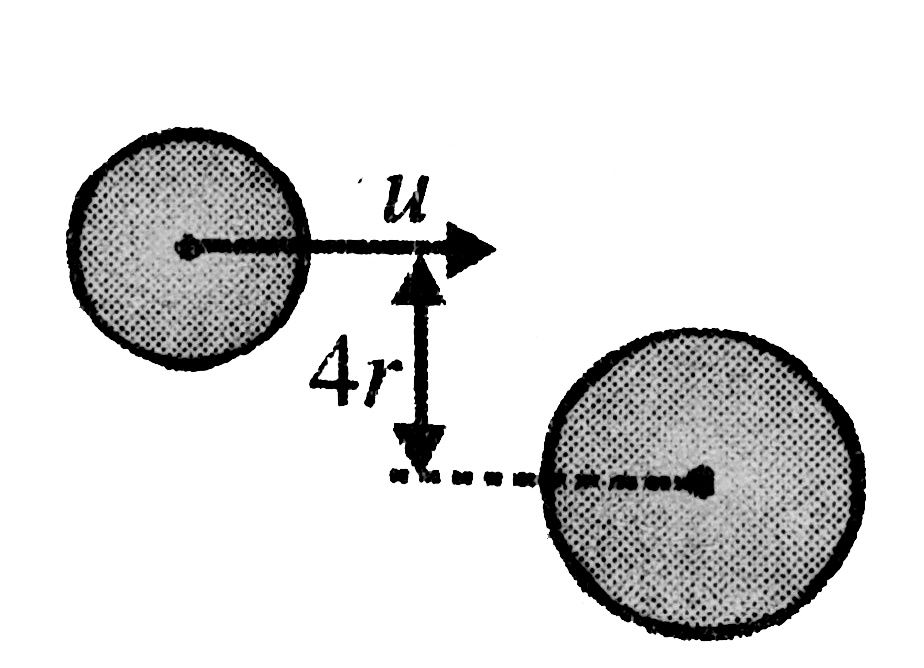 What is the final velocity of the heavier disc?
What is the final velocity of the heavier disc?
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

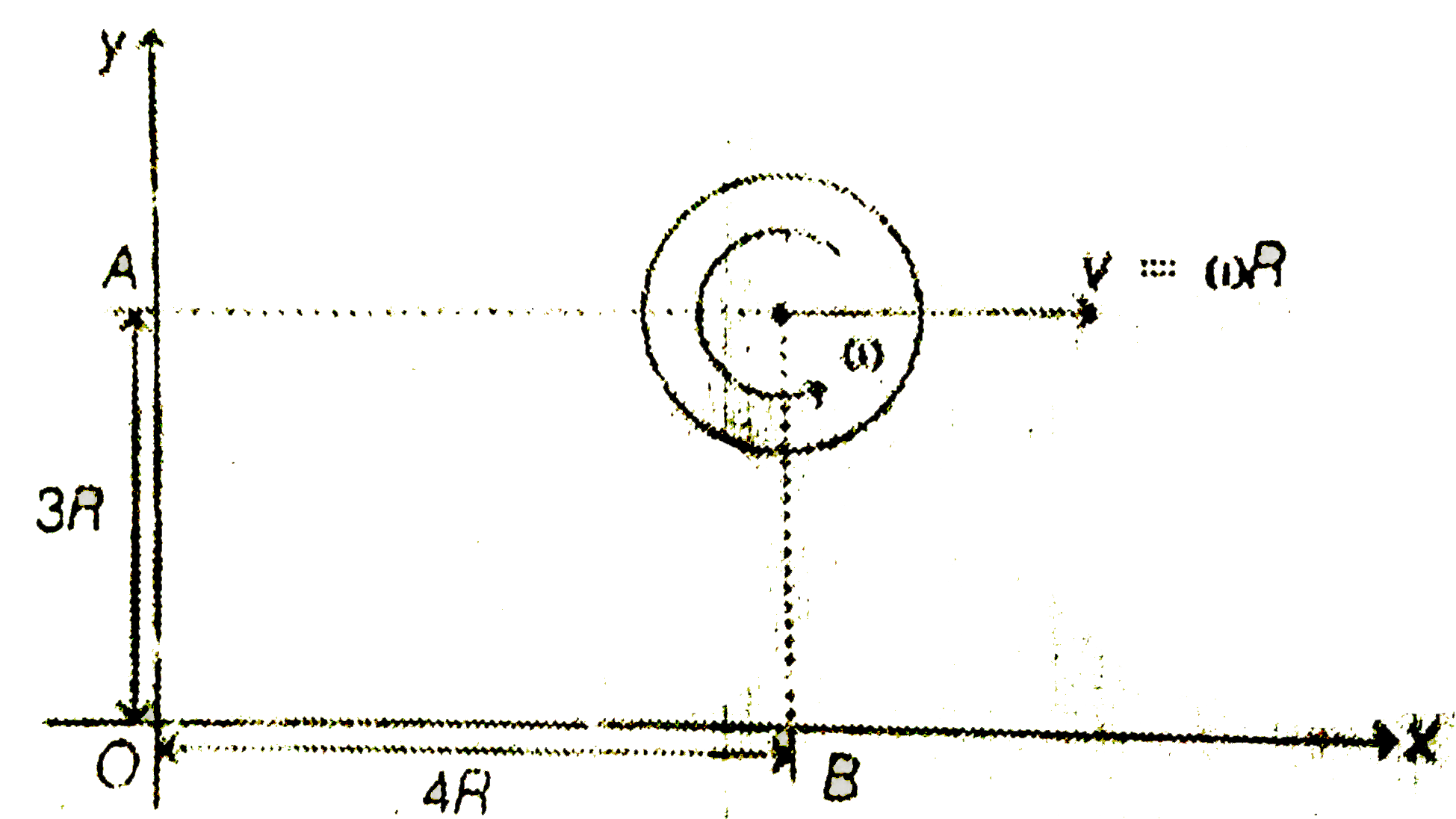
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionA small smooth disc of mass m and radius moving with an initial velocity 'v' along the positive x− axis collided with a big disc of mass 2m and radius 2r which was initially at rest with its centre at origin as shown in figure.

If the coefficient of restitution is 0 then velocity of larger disc after collision is
View Solution
Two identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
View SolutionA circular disc of mass M and radius R rotating with speed of ω and another disc of same mass M and radius R/2 placed co axially on first disc, after sometime disc-2 also attain constant speed w2 . Find loss of percentage in energy
View Solution
