A point lilke paticle of mass 'm' (very small) is projected in the vertically upward direction where already exists, a uniform horizontal electric field ¯¯¯E. The field strength is such that qE=34mg, where q is the charge on the particle. After what time the radius of curvature of the charged particle will be minimum.
V0g
8V025g
16V025g
25V016g
The correct Answer is:C
To solve the problem, we need to find the time at which the radius of curvature of a charged particle projected vertically upward in a uniform horizontal electric field is minimized. We are given that the electric force acting on the particle is qE=34mg.
1. Identify Forces Acting on the Particle:
- The weight of the particle W=mg acts downward.
- The electric force FE=qE acts horizontally. Given qE=34mg, we can denote this force as FE=34mg.
2. Calculate the Net Force:
- The net force acting on the particle can be found using the Pythagorean theorem since the forces are perpendicular to each other:
Fnet=√(FE)2+(W)2=√(34mg)2+(mg)2
- Simplifying this:
Fnet=√(916m2g2)+(m2g2)=√916m2g2+1616m2g2=√2516m2g2=54mg
3. Determine Acceleration:
- The net acceleration a acting on the particle can be calculated using Newton's second law F=ma:
a=Fnetm=54mgm=54g
4. Understanding the Motion:
- The particle is projected upward with an initial velocity v0. The motion can be analyzed in two components: vertical and horizontal.
- The vertical component of the velocity will decrease due to gravity and the upward motion until it reaches zero.
5. Finding the Angle:
- The angle θ between the vertical and the net force can be found using:
tanθ=FEW=34mgmg=34
- Therefore, θ=tan−1(34).
6. Finding Minimum Radius of Curvature:
- The radius of curvature R is given by:
R=V2A⊥
- To minimize R, we need to minimize the vertical component of the velocity Vsinθ.
7. Setting Up the Equation for Time:
- The vertical motion can be described by:
Vsinθ−at=0
- Substituting a=54g and sinθ=45 (from the triangle formed by the forces):
V0sin53∘−54gt=0
- Rearranging gives:
t=V0sin53∘54g
8. Final Calculation:
- Substituting sin53∘=45:
t=V0⋅4554g=16V025g
Conclusion:
The time after which the radius of curvature of the charged particle will be minimum is:
t=16V025g
- The weight of the particle W=mg acts downward.
- The electric force FE=qE acts horizontally. Given qE=34mg, we can denote this force as FE=34mg.
- The net force acting on the particle can be found using the Pythagorean theorem since the forces are perpendicular to each other:
Fnet=√(FE)2+(W)2=√(34mg)2+(mg)2
- Simplifying this:
Fnet=√(916m2g2)+(m2g2)=√916m2g2+1616m2g2=√2516m2g2=54mg
- The net acceleration a acting on the particle can be calculated using Newton's second law F=ma:
a=Fnetm=54mgm=54g
- The particle is projected upward with an initial velocity v0. The motion can be analyzed in two components: vertical and horizontal.
- The vertical component of the velocity will decrease due to gravity and the upward motion until it reaches zero.
- The angle θ between the vertical and the net force can be found using:
tanθ=FEW=34mgmg=34
- Therefore, θ=tan−1(34).
- The radius of curvature R is given by:
R=V2A⊥
- To minimize R, we need to minimize the vertical component of the velocity Vsinθ.
- The vertical motion can be described by:
Vsinθ−at=0
- Substituting a=54g and sinθ=45 (from the triangle formed by the forces):
V0sin53∘−54gt=0
- Rearranging gives:
t=V0sin53∘54g
- Substituting sin53∘=45:
t=V0⋅4554g=16V025g
The time after which the radius of curvature of the charged particle will be minimum is:
t=16V025g
Similar Questions
A particle of mass 2 kg charge 1 mC is projected vertially with velocity k10ms−1. There is as uniform horizontal electric field of 104N/C, then
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of mass m carries an electric positive charge Q and is subjected to the combined action of gravity g and a uniform horizontal electric field of strength E,it is projected with speed u to the vertical plane parallel to the electrical field and at an angle θto the horizontal .The maximum distance the particle travels horizontally when it is at the same level as its starting point is
View SolutionA particle of charge q0 and of mass m0 is projected along the y-axis at t=0 from origin with a velocity V0. If a uniform electric field E0 also exist along the x-axis, then the time at which debroglie wavelength of the particle becomes half of the initial value is:
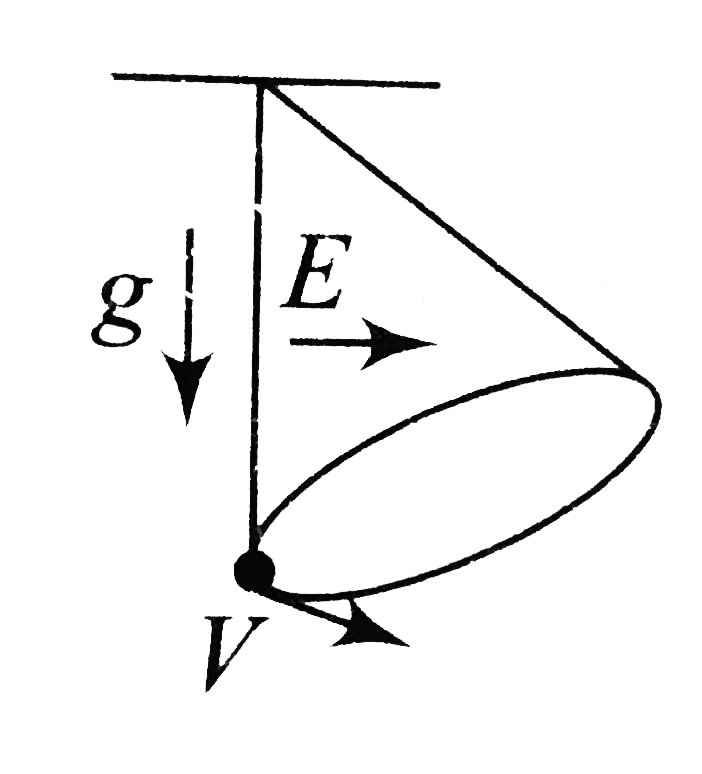
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
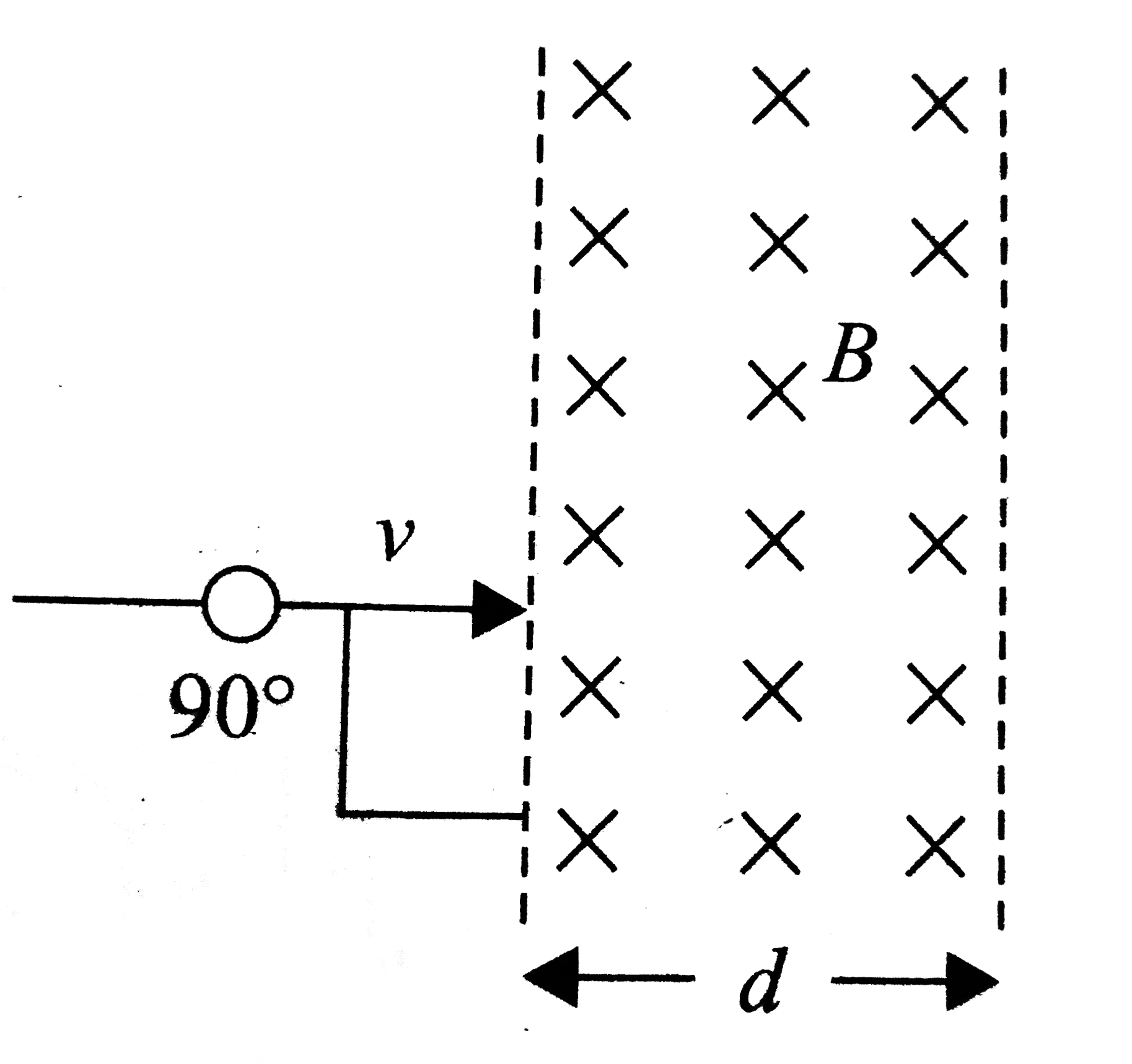
View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA particle of mass m and positive charge q is projected with a speed of v0 in y–direction in the presence of electric and magnetic field are in x–direction. Find the instant of time at which the speed of particle becomes double the initial speed.
View Solution
