Galvanic cells generate electrical energy at the expense of a spontaneous redox reaction. In an electrode concentration cell two like electrodes having different concentrations, either because they are gas electrodes operating at different pressures or because they are amalgams (solutions in mercury) with different concentrations are dipped into the same solution.
Eg. An example is a cell composed of two chlorine electrodes with different pressure of Cl2:
PtL|Cl2(PL)|HCl(aq)|Cl2(PR)|PtR
Where PL and PR are the Cl2 pressure at the left and right electrodes.
Calculate the EMF of the electrode concentration cell represented by :
Hg−Zn(c1)∣∣Zn+2(aq)∣∣Hg−Zn(c2)
At 25∘C.c1=2g of Zn per 100g of Hg and c2=1g of Zn per 50g of Hg
0.059V
3
0
data insufficient
The correct Answer is:C
To calculate the EMF of the electrode concentration cell represented by Hg−Zn(c1)∣∣Zn+2(aq)∣∣Hg−Zn(c2), we will follow these steps:
Step 1: Understand the Concentration Cell
In a concentration cell, the EMF is generated due to the difference in concentration of the same species on both sides of the cell. Here, we have zinc in mercury amalgam at two different concentrations.
Step 2: Identify the Given Concentrations
- For the left electrode (anode), c1=2g of Zn per 100g of Hg.
- For the right electrode (cathode), c2=1g of Zn per 50g of Hg.
Step 3: Convert Concentrations to Molarity
To compare the concentrations, we need to express them in the same unit. We can convert the given concentrations into molarity (moles per liter).
1. Calculate the molar mass of zinc (Zn):
- Molar mass of Zn = 65.38 g/mol.
2. Calculate the concentration at the anode (c1):
- c1=(2gZn100gHg)⋅(1molZn65.38gZn)=(2100)⋅(165.38)molZnpergHg.
- Since we need to express it in terms of moles per liter, we can assume the density of mercury is approximately 13.6 g/cm³, which is 13600 g/L.
- Therefore, the concentration in molarity is:
\(
c_{1} = \frac{(2/100) \times (1/65.38)}{(100/13600)} = \frac{2 \times 13600}{100 \times 65.38} \text{ mol/L}
\)
3. Calculate the concentration at the cathode (c2):
- c2=(1gZn50gHg)⋅(1molZn65.38gZn)=(150)⋅(165.38)molZnpergHg.
- Similarly, using the density of mercury:
\(
c_{2} = \frac{(1/50) \times (1/65.38)}{(50/13600)} = \frac{1 \times 13600}{50 \times 65.38} \text{ mol/L}
\)
Step 4: Apply the Nernst Equation
The Nernst equation for a concentration cell is given by:
\(
E_{cell} = E^{\circ} + \frac{RT}{nF} \ln \left( \frac{(Zn^{2+})_{anode}}{(Zn^{2+})_{cathode}} \right)
\)
Where:
- \( R = 8.314 \, J/(mol \cdot K) \)
- \( T = 298 \, K \) (25°C)
- \( n = 2 \) (for Zn)
- \( F = 96485 \, C/mol \)
Since both electrodes are zinc, \( E^{\circ} = 0 \).
Step 5: Calculate the EMF
Substituting the values:
\(
E_{cell} = 0 + \frac{(8.314)(298)}{2(96485)} \ln \left( \frac{c_{1}}{c_{2}} \right)
\)
Step 6: Evaluate the Concentration Ratio
Since we have already calculated the concentrations:
- \( c_{1} = \frac{2 \times 13600}{100 \times 65.38} \)
- \( c_{2} = \frac{1 \times 13600}{50 \times 65.38} \)
Now, simplify the ratio \( \frac{c_{1}}{c_{2}} \):
\(
\frac{c_{1}}{c_{2}} = \frac{(2/100)}{(1/50)} = \frac{2 \times 50}{100 \times 1} = 1
\)
Step 7: Conclusion
Since \( \ln(1) = 0 \), the EMF becomes:
\(
E_{cell} = 0
\)
Final Answer
The EMF of the electrode concentration cell is 0 V.
---
In a concentration cell, the EMF is generated due to the difference in concentration of the same species on both sides of the cell. Here, we have zinc in mercury amalgam at two different concentrations.
- For the left electrode (anode), c1=2g of Zn per 100g of Hg.
- For the right electrode (cathode), c2=1g of Zn per 50g of Hg.
To compare the concentrations, we need to express them in the same unit. We can convert the given concentrations into molarity (moles per liter).
- Molar mass of Zn = 65.38 g/mol.
- c1=(2gZn100gHg)⋅(1molZn65.38gZn)=(2100)⋅(165.38)molZnpergHg.
- Since we need to express it in terms of moles per liter, we can assume the density of mercury is approximately 13.6 g/cm³, which is 13600 g/L.
- Therefore, the concentration in molarity is:
\(
c_{1} = \frac{(2/100) \times (1/65.38)}{(100/13600)} = \frac{2 \times 13600}{100 \times 65.38} \text{ mol/L}
\)
- c2=(1gZn50gHg)⋅(1molZn65.38gZn)=(150)⋅(165.38)molZnpergHg.
- Similarly, using the density of mercury:
\(
c_{2} = \frac{(1/50) \times (1/65.38)}{(50/13600)} = \frac{1 \times 13600}{50 \times 65.38} \text{ mol/L}
\)
The Nernst equation for a concentration cell is given by:
\(
E_{cell} = E^{\circ} + \frac{RT}{nF} \ln \left( \frac{(Zn^{2+})_{anode}}{(Zn^{2+})_{cathode}} \right)
\)
Where:
- \( R = 8.314 \, J/(mol \cdot K) \)
- \( T = 298 \, K \) (25°C)
- \( n = 2 \) (for Zn)
- \( F = 96485 \, C/mol \)
Substituting the values:
\(
E_{cell} = 0 + \frac{(8.314)(298)}{2(96485)} \ln \left( \frac{c_{1}}{c_{2}} \right)
\)
Since we have already calculated the concentrations:
- \( c_{1} = \frac{2 \times 13600}{100 \times 65.38} \)
- \( c_{2} = \frac{1 \times 13600}{50 \times 65.38} \)
\(
\frac{c_{1}}{c_{2}} = \frac{(2/100)}{(1/50)} = \frac{2 \times 50}{100 \times 1} = 1
\)
Since \( \ln(1) = 0 \), the EMF becomes:
\(
E_{cell} = 0
\)
The EMF of the electrode concentration cell is 0 V.
Similar Questions
For the half cell
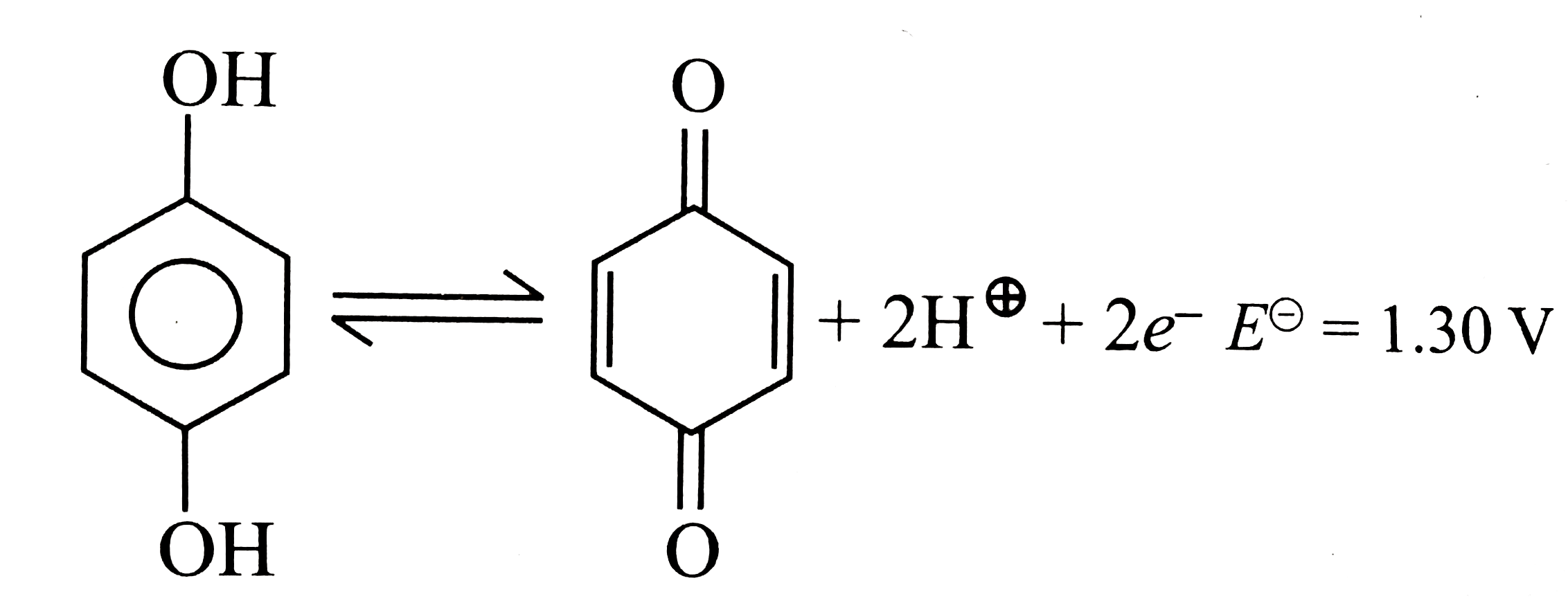
At pH=2, the electrode potential is
View SolutionDuring the electrolysis of aqueous nitric acid solution using Pt electrodes
View SolutionPt(Cl2)(p1)|HCl(0.1M)|(Cl2)(p2),Pt cell reaction will be endergonic if
View SolutionPt(Cl2)(p1)|HCl(0.1M)|(Cl2)(p2),Pt cell reaction will be endergonic if
View SolutionWhen a cell is placed in the solution of different concentration then , the cell swells in.... and shrink in .... respectively.
View SolutionWhen an aqueous concentrated solution of lithium chloride is electrolysed using inert electrodes:
View SolutionIn the operation of a galvanic cell, at one of the electrodes, oxidation takes place. What is the name of this electrode and what is its polarity?
View SolutionThe products of electrolysis of CuSO4(aq) between two Pt electrodes
View SolutionWhen the positive and negative electrodes of a cell are denoted as P and N inside the cell.
View SolutionWrite the electrode reactions in Nelson's cell.
View Solution

