Two moles of an ideal monoatomic gas undergoes a process VT= constant. If temperature of the gas is increased by ΔT=300K, then the ratio (ΔUΔQ) is
2
3
4
6
The correct Answer is:B
To solve the problem, we need to find the ratio ΔUΔQ for a process where VT=constant and the temperature of the gas is increased by ΔT=300K.
1. Identify the type of gas and its properties:
We have 2 moles of an ideal monoatomic gas. For a monoatomic gas, the degrees of freedom f=3.
2. Calculate the change in internal energy (ΔU):
The change in internal energy for an ideal gas is given by the formula:
ΔU=f2nRΔT
For a monoatomic gas, f=3, and we have n=2 moles. Therefore:
ΔU=32×2×R×300
Simplifying this, we get:
ΔU=3×R×300=900R
3. Determine the work done (W) during the process:
For the process VT=constant, we can use the relation for work done:
W=nRΔT1−η
Here, η=2 (since VT implies PV2=constant), so:
W=nRΔT1−2=nR300−1=−300nR
Substituting n=2:
W=−600R
4. Calculate the heat added (ΔQ):
According to the first law of thermodynamics:
ΔQ=ΔU+W
Substituting the values we found:
ΔQ=900R−600R=300R
5. Calculate the ratio ΔUΔQ:
Now we can find the ratio:
ΔUΔQ=900R300R=3
Final Answer:
ΔUΔQ=3
We have 2 moles of an ideal monoatomic gas. For a monoatomic gas, the degrees of freedom f=3.
The change in internal energy for an ideal gas is given by the formula:
ΔU=f2nRΔT
For a monoatomic gas, f=3, and we have n=2 moles. Therefore:
ΔU=32×2×R×300
Simplifying this, we get:
ΔU=3×R×300=900R
For the process VT=constant, we can use the relation for work done:
W=nRΔT1−η
Here, η=2 (since VT implies PV2=constant), so:
W=nRΔT1−2=nR300−1=−300nR
Substituting n=2:
W=−600R
According to the first law of thermodynamics:
ΔQ=ΔU+W
Substituting the values we found:
ΔQ=900R−600R=300R
Now we can find the ratio:
ΔUΔQ=900R300R=3
ΔUΔQ=3
Similar Questions
An ideal monatomic gas undergoes process PV1.25 = constant .Then
View SolutionTwo moles of an ideal diatomic gas is taken through a process VT2= constant so that its temperature increases by ΔT=300K. The ratio (ΔUΔQ) of increase in internal energy and heat supplied to the gas during the process is
View SolutionWhich one of the following is correctly matched ?
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process, as shown in the figure. If the temperature of the gas at state 1 is 300 K and at state 4 is 500 K, then heat exchanged during process 2→3, is
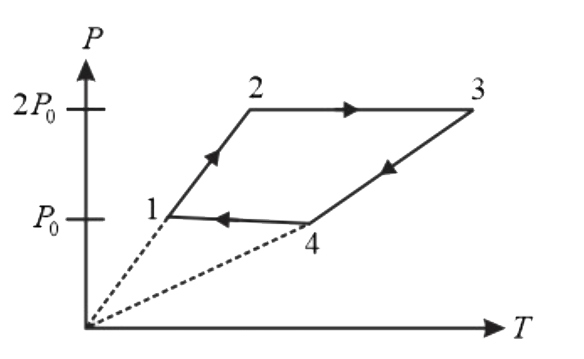
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
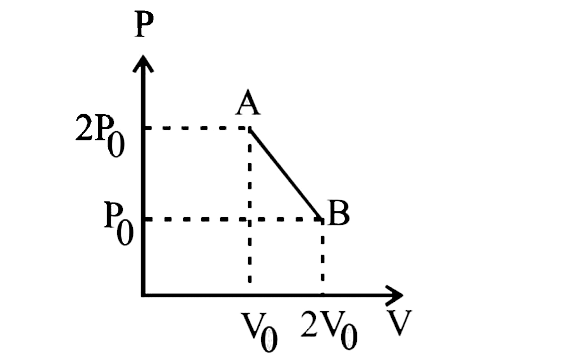
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View SolutionIn a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View Solution
