A parallel beam of light of wavelength λ passes through a slit of width d. The transmitted light is collected on a screen D aways (D>>d). Find the distance between the two second order minima.
Dλd
Dλ2d
2Dλd
4Dλd
The correct Answer is:D
To find the distance between the two second order minima in a single slit diffraction pattern, we can follow these steps:
Step 1: Understand the condition for minima
In single slit diffraction, the condition for minima is given by:
dsinθ=nλ
where:
- d is the width of the slit,
- θ is the angle of the minima,
- n is the order of the minima (for second order, n=2),
- λ is the wavelength of the light.
Step 2: Substitute for second order minima
For the second order minima, we set n=2:
dsinθ=2λ
Step 3: Use the small angle approximation
Since the distance D from the slit to the screen is much larger than the slit width d (i.e., D≫d), we can use the small angle approximation:
sinθ≈tanθ≈θ
Thus, we can rewrite the equation as:
dθ=2λ
Step 4: Solve for θ
From the above equation, we can solve for θ:
θ=2λd
Step 5: Relate y to D and θ
The position y of the minima on the screen can be related to D and θ using:
y=Dtanθ
Since tanθ≈θ for small angles, we have:
y≈Dθ
Step 6: Substitute θ into the equation for y
Substituting θ into the equation gives:
y≈D(2λd)=2λDd
Step 7: Find the distance between the two second order minima
Since there are two second order minima (one on each side of the central maximum), the distance between them is:
Distance between two second order minima=2y=2(2λDd)=4λDd
Final Result
The distance between the two second order minima is:
4λDd
---
In single slit diffraction, the condition for minima is given by:
dsinθ=nλ
where:
- d is the width of the slit,
- θ is the angle of the minima,
- n is the order of the minima (for second order, n=2),
- λ is the wavelength of the light.
For the second order minima, we set n=2:
dsinθ=2λ
Since the distance D from the slit to the screen is much larger than the slit width d (i.e., D≫d), we can use the small angle approximation:
sinθ≈tanθ≈θ
Thus, we can rewrite the equation as:
dθ=2λ
From the above equation, we can solve for θ:
θ=2λd
The position y of the minima on the screen can be related to D and θ using:
y=Dtanθ
Since tanθ≈θ for small angles, we have:
y≈Dθ
Substituting θ into the equation gives:
y≈D(2λd)=2λDd
Since there are two second order minima (one on each side of the central maximum), the distance between them is:
Distance between two second order minima=2y=2(2λDd)=4λDd
The distance between the two second order minima is:
4λDd
Similar Questions
A parallel beam of green light of wavelength 546 nm passes through a slit of width 0.40mm. The transmitted light is collected on a screen 40 cm away. Find the distance between the two first order minima.
View SolutionA parallel beam of monochromatic light of wavelength 450 nm passes through a long slit of width 0.2 mm. find the angular divergence in which most of the light is diffracted.
View Solution
Knowledge Check
A parallel beam of light of wavelength 600 nm is incident normally on a slit of width d. If the distance between the slits and the screen is 0.8 m and the distance of 2nd order maximum from the centre of the screen is 15 mm. The width of the slit is
A40μmB80μmC160μmD200μmA parallel beam of light of wavelength 6000Å gets diffracted by a single slit of width 0.3 mm. The angular position of the first minima of diffracted light is :
A2×10−3radB3×10−3radC1.8×10−3radD6×10−3rad
A parallel beam of monochromatic light of wavelength 450 nm passes through a long slit of width 0.2 mm. find the angular divergence in which most of the light is diffracted.
View SolutionIn a single slit diffraction of light of wavelength λ by a slit of width e, the size of the central maximum on a screen at a distance b is
View SolutionTwo ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
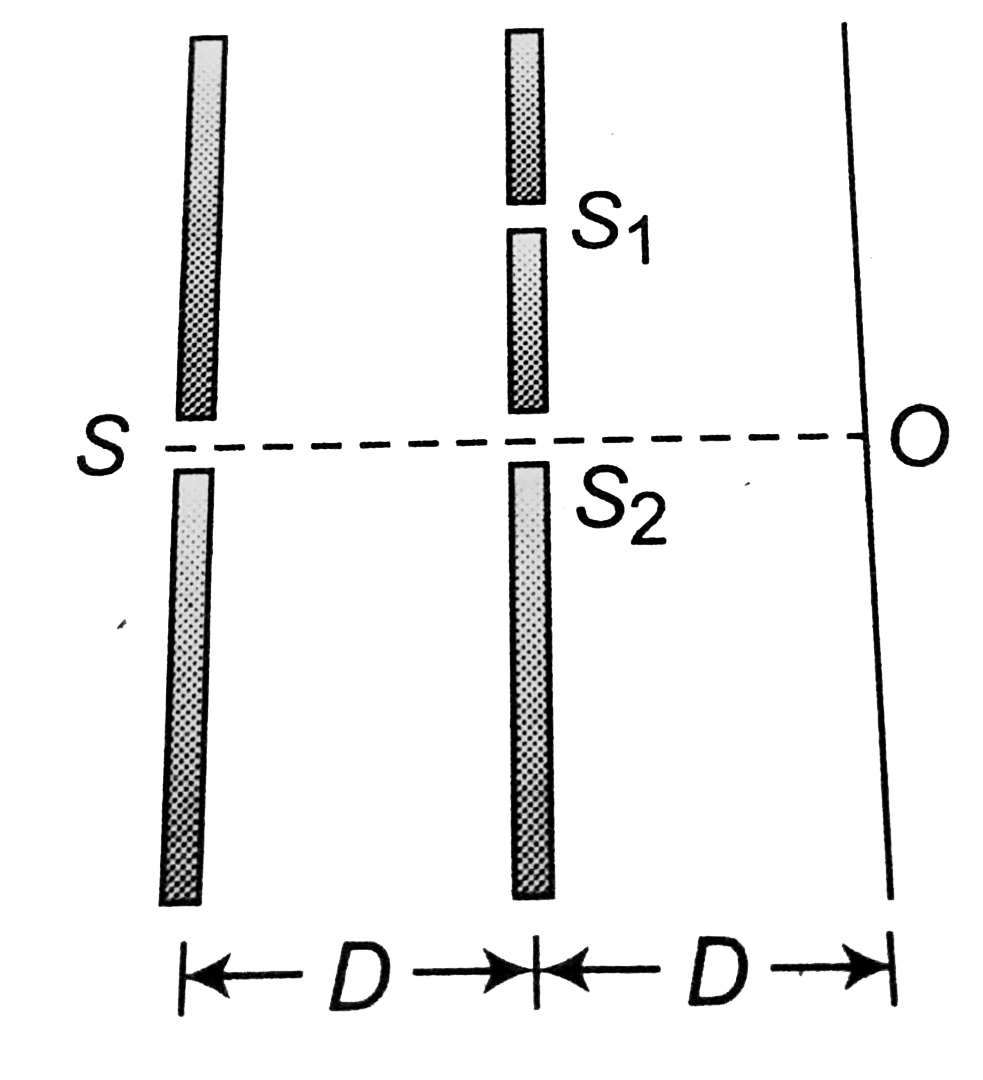
View SolutionA beam of light of wavelength 400 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 2 m away from the slit. It is observed that 2nd order minima occurs at a distance of 2 mm from the position of central maxima. Find the width of the slit.
View SolutionConsider the situation shown in figure. The two slite S1andS2
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen M1 placed at a distance D from the slits. The slit S3 is
at the centre line and the slit S4 is at a distance y form S3. Another screen M2 is
placed at a further distance D away from M1. Find the ration of the maximum to
minimum intensity observed on M2 if y is equal to (d<<D).
View SolutionLight of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is
View Solution

