A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion is
mg2k
mgk
L/2
L
The correct Answer is:B
To solve the problem, we need to determine the largest amplitude Amax for which the inelastic string remains taut during the oscillation of the mass m attached to the spring with spring constant k.
1. Understanding the System:
- We have a mass m attached to a spring with spring constant k via an inelastic string of length L.
- The mass is initially at rest, and we need to analyze its motion when it oscillates.
2. Condition for the String to Remain Taut:
- For the string to remain taut, the tension in the string must not become zero at any point during the oscillation.
- This means that when the mass is at its maximum displacement (amplitude), the spring must be stretched such that the force exerted by the spring equals the weight of the mass.
3. Applying Hooke's Law:
- According to Hooke's law, the force exerted by the spring when it is stretched by a distance x is given by:
Fspring=kx
- At maximum amplitude Amax, the force exerted by the spring must balance the weight of the mass:
kx=mg
4. Finding the Maximum Displacement:
- From the equation kx=mg, we can solve for x:
x=mgk
- This x represents the maximum stretch of the spring when the mass is at its lowest point.
5. Conclusion:
- Since the maximum amplitude Amax must be equal to the maximum stretch x for the string to remain taut, we have:
Amax=mgk
Final Answer:
The largest amplitude Amax for which the string will remain taut throughout the motion is:
Amax=mgk
- We have a mass m attached to a spring with spring constant k via an inelastic string of length L.
- The mass is initially at rest, and we need to analyze its motion when it oscillates.
- For the string to remain taut, the tension in the string must not become zero at any point during the oscillation.
- This means that when the mass is at its maximum displacement (amplitude), the spring must be stretched such that the force exerted by the spring equals the weight of the mass.
- According to Hooke's law, the force exerted by the spring when it is stretched by a distance x is given by:
Fspring=kx
- At maximum amplitude Amax, the force exerted by the spring must balance the weight of the mass:
kx=mg
- From the equation kx=mg, we can solve for x:
x=mgk
- This x represents the maximum stretch of the spring when the mass is at its lowest point.
- Since the maximum amplitude Amax must be equal to the maximum stretch x for the string to remain taut, we have:
Amax=mgk
The largest amplitude Amax for which the string will remain taut throughout the motion is:
Amax=mgk
Similar Questions
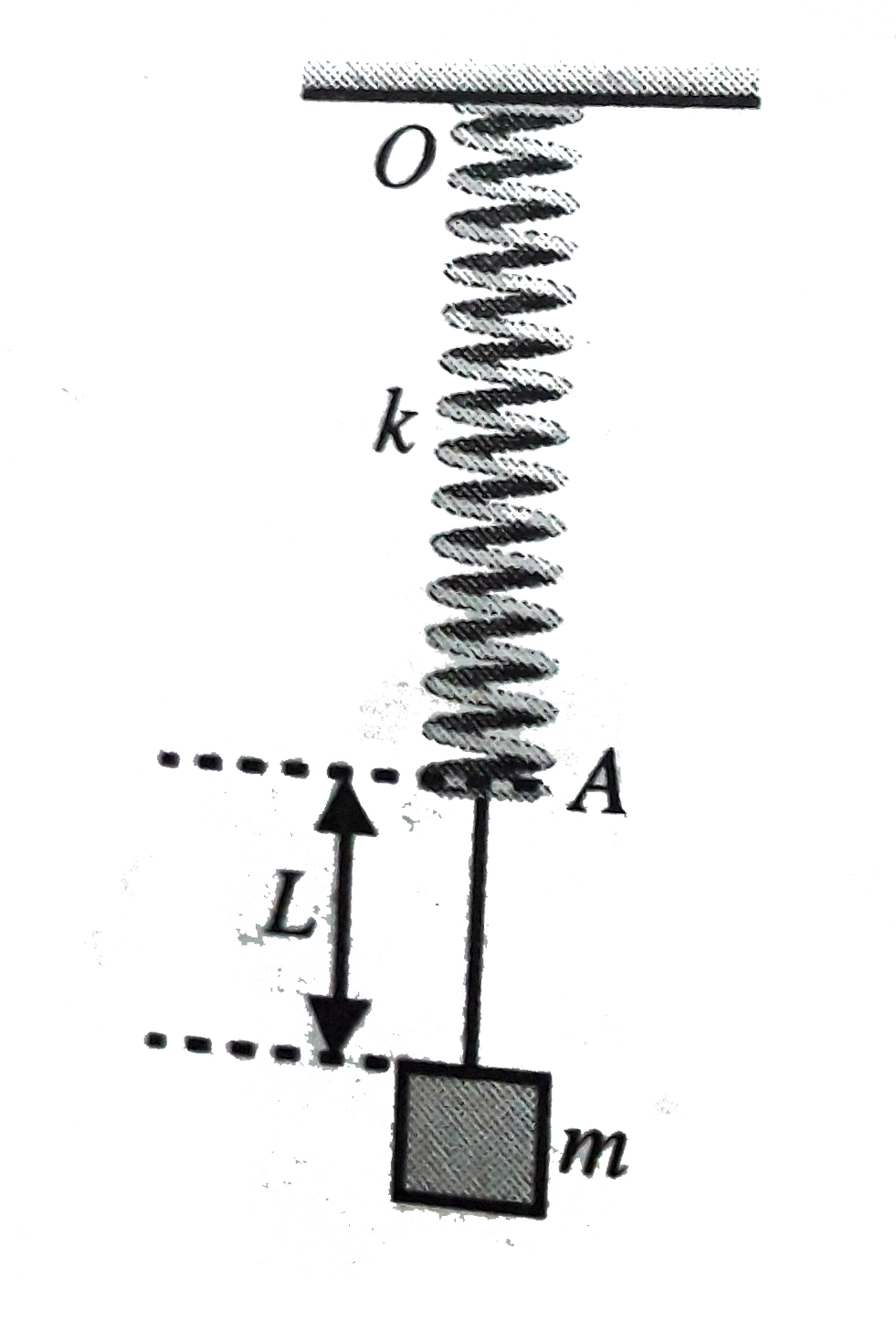
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will be
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
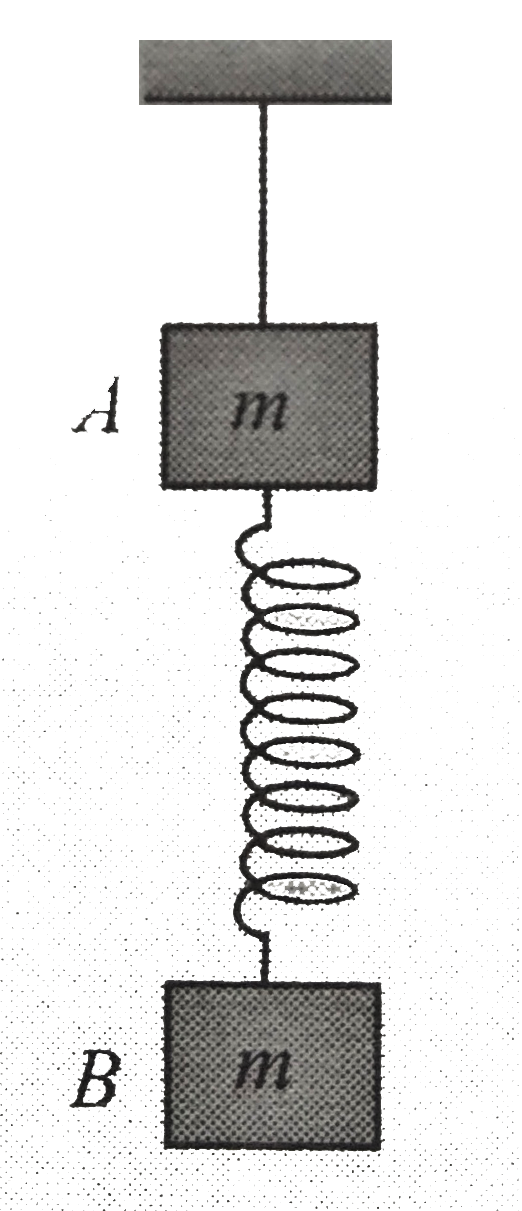
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionThe block of mass m is at rest. Find the tension in the string A .

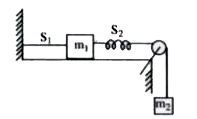
View SolutionTwo blocks m1andm2 are in equilibrium. S1 is a string and S2 is a spring of spring constant k. Immediately after the string S1 is cut,
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a function of the distance measured from the mass M (bottom of the string).

View Solution