A capacitor is made of two concentric spherical shells A and B of radii a and b respectively. Where . The external shell B is grounded Inner shel i.e is filled with a uniform positive charge of density . Variation of electric field versus distance from the centre.
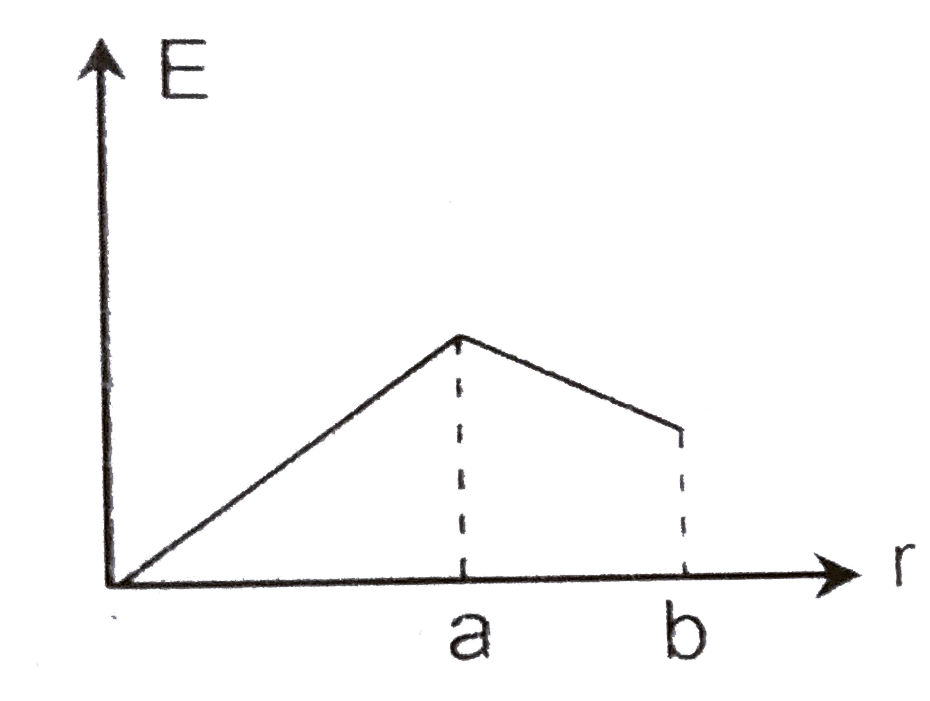
The correct Answer is:B
To solve the problem of finding the variation of the electric field versus distance from the center for the given capacitor made of two concentric spherical shells, we can follow these steps:
1. Understanding the Configuration:
- We have two concentric spherical shells: inner shell A with radius a and outer shell B with radius b.
- The outer shell B is grounded, meaning its potential VB=0.
- The inner shell A is filled with a uniform positive charge density ρ.
2. Applying Gauss's Law:
- To find the electric field E at a distance r from the center, we can use Gauss's law, which states:
∮E⋅dA=Qencϵ0
- Here, Qenc is the charge enclosed by a Gaussian surface of radius r.
3. Case 1: Inside the Inner Shell ( r<a ):
- For r<a, there is no charge enclosed within this Gaussian surface, so:
Qenc=0⟹E=0
4. Case 2: Within the Inner Shell ( a≤r<b ):
- For a≤r<b, we need to calculate the charge enclosed within a sphere of radius r:
Qenc=ρ⋅Volume of sphere with radius r=ρ⋅43πr3
- Applying Gauss's law:
E⋅4πr2=ρ⋅43πr3ϵ0
- Simplifying this gives:
E=ρr3ϵ0
5. Case 3: Outside the Outer Shell ( r≥b ):
- For r≥b, since the outer shell B is grounded, the electric field outside the shell will be zero:
E=0
6. Summary of Electric Field Variation:
- For r<a: E=0
- For a≤r<b: E=ρr3ϵ0 (linear increase with r)
- For r≥b: E=0
Final Result:
The electric field E varies as follows:
- E=0 for r<a
- E=ρr3ϵ0 for a≤r<b
- E=0 for r≥b
- We have two concentric spherical shells: inner shell A with radius a and outer shell B with radius b.
- The outer shell B is grounded, meaning its potential VB=0.
- The inner shell A is filled with a uniform positive charge density ρ.
- To find the electric field E at a distance r from the center, we can use Gauss's law, which states:
∮E⋅dA=Qencϵ0
- Here, Qenc is the charge enclosed by a Gaussian surface of radius r.
- For r<a, there is no charge enclosed within this Gaussian surface, so:
Qenc=0⟹E=0
- For a≤r<b, we need to calculate the charge enclosed within a sphere of radius r:
Qenc=ρ⋅Volume of sphere with radius r=ρ⋅43πr3
- Applying Gauss's law:
E⋅4πr2=ρ⋅43πr3ϵ0
- Simplifying this gives:
E=ρr3ϵ0
- For r≥b, since the outer shell B is grounded, the electric field outside the shell will be zero:
E=0
- For r<a: E=0
- For a≤r<b: E=ρr3ϵ0 (linear increase with r)
- For r≥b: E=0
The electric field E varies as follows:
- E=0 for r<a
- E=ρr3ϵ0 for a≤r<b
- E=0 for r≥b
Similar Questions
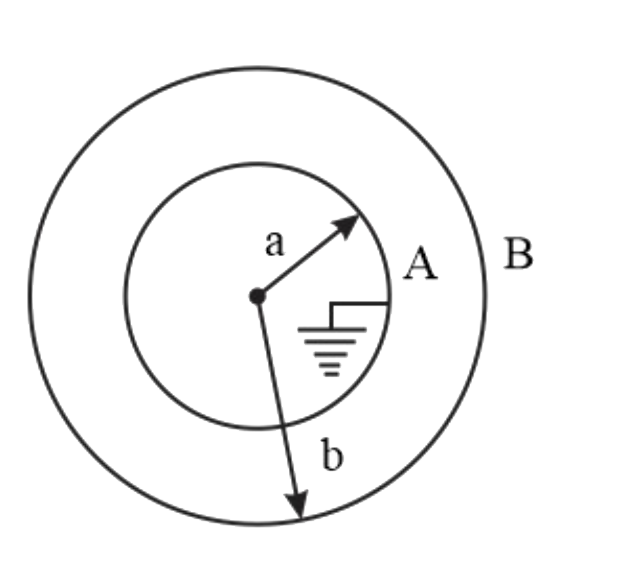
The equivalent capacitance between A and B, where two concentric spherical shells having radius a and b are connected as shown in the figure.
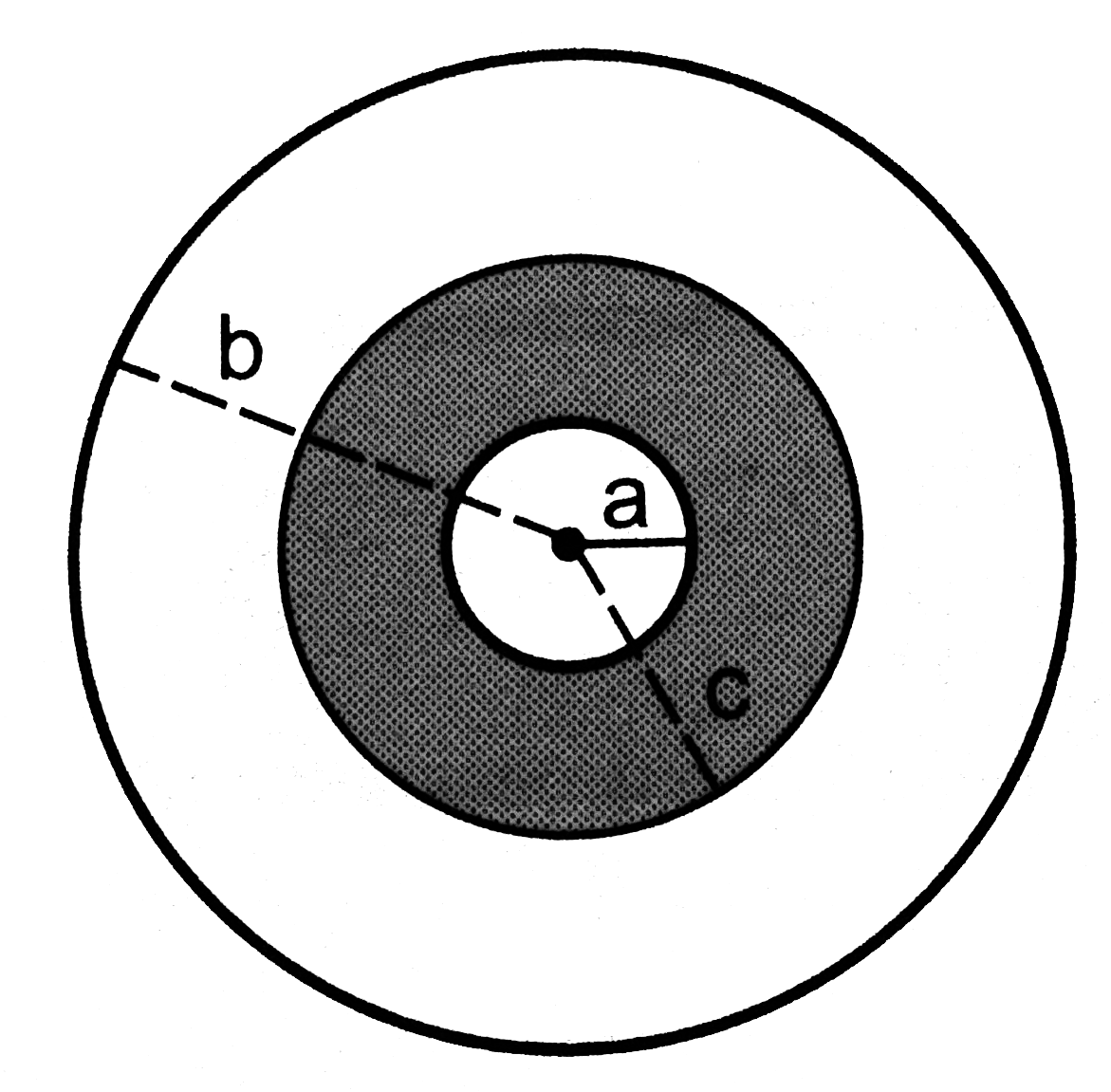
View SolutionA sphercial capacitor is made of two conducting spherical shells of radii a and b.The space between the shells is filled with a dielectric constant Kup to a radius c as shown in figure. Calculate the capacitance .
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b, and c. The shells A and C are given charge q and -q, respectively, and shell B is earthed. Then,
View SolutionA and B are two concentric spherical shells. If A is given a charge +Q while B is earthed as shown in figure then
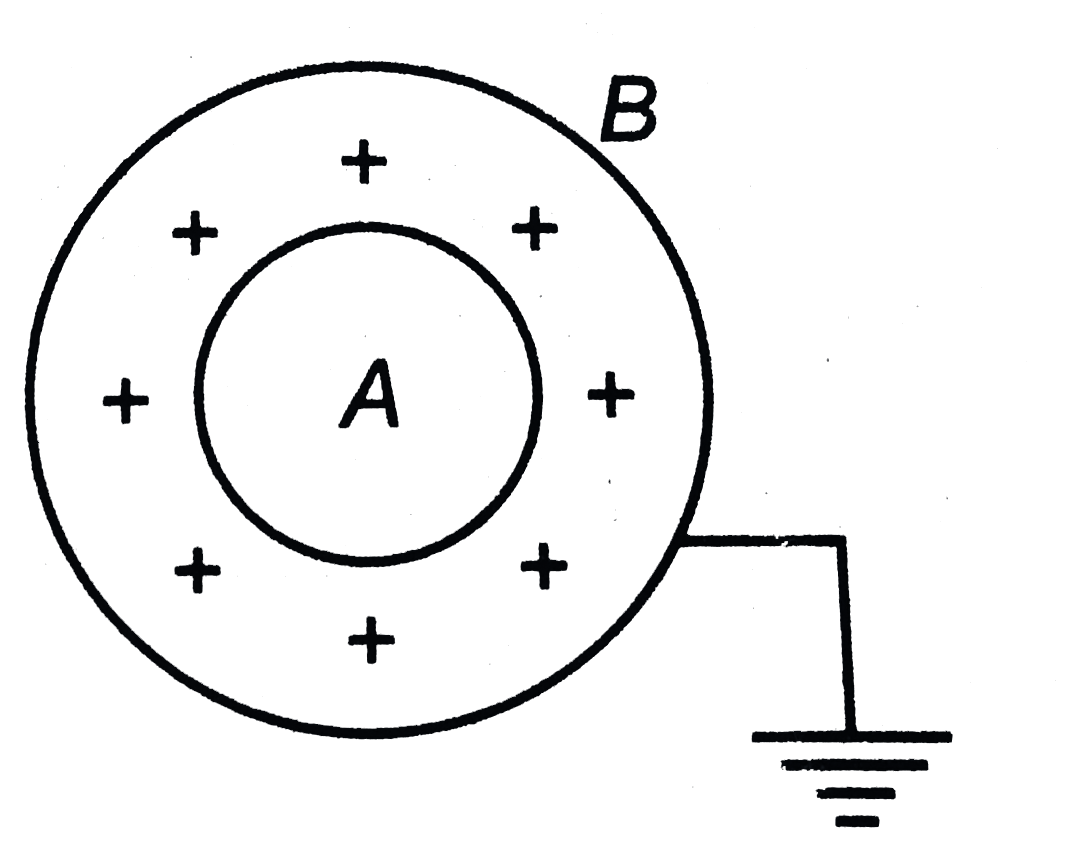
View SolutionA and B are two concentric spherical shells. If A is given a charge +q while B is earthed as shown in figure then

View SolutionFigure shows a system of three concentric metal shells, A, B and C with radii a, 2a and 3a respectively. Shell B is earthed and shell C is given a charge Q. Now if shell C is connected to shell A, then find the final charge on the shell B

View SolutionFour concentric conducting spherical shells A, B, C and D of radii a, 2a, 3a and 4a respectively. Shell B and D are given charges q and −q respectively. If shell C is grounded then potential difference (VA — VC) is
View SolutionThere are two concentric metallic spherical shells of radii a and b such that a < b. An ideal cell of emf is connected across the two shells. The medium between the sheets is filled with a dielectric of dielectric constant and resistivity p. For a point P at a distance from the common centre C where a < r< b. Now choose INCORRECT option.
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View Solution

