Power emitted per unit area of a black body is R watt/m2. At what wavelength will the power radiated by black body be maximum is stefan's constant is σ and Wien's constant is b then.
λ=(bσR)14
λ=(bR)14
(bRσ)14=λ
λ=b(σR)14
The correct Answer is:D
To solve the problem of finding the wavelength at which the power radiated by a black body is maximum, we can follow these steps:
1. Understand the Problem: We need to find the wavelength (λ_max) at which the power emitted per unit area of a black body is maximum, given the power emitted (R), Stefan's constant (σ), and Wien's constant (b).
2. Use Stefan-Boltzmann Law: According to the Stefan-Boltzmann law, the power radiated per unit area (P) of a black body is given by:
P=σT4
where T is the absolute temperature of the black body.
3. Relate Temperature to Power: Rearranging the equation gives us the temperature in terms of power:
T=(Rσ)1/4
4. Apply Wien's Displacement Law: Wien's displacement law states that the product of the temperature (T) and the wavelength at which the emission is maximum (λ_max) is a constant:
T⋅λmax=b
where b is Wien's constant.
5. Substitute for Temperature: Substitute the expression for temperature (T) from step 3 into the equation from step 4:
(Rσ)1/4⋅λmax=b
6. Solve for λ_max: Rearranging the equation to solve for λ_max gives:
λmax=b⋅σ1/4R1/4
Final Expression:
Thus, the wavelength at which the power radiated by the black body is maximum is given by:
λmax=b⋅σ1/4R1/4
Conclusion:
After analyzing the options provided in the question, we can conclude that option D is the correct answer.
P=σT4
where T is the absolute temperature of the black body.
T=(Rσ)1/4
T⋅λmax=b
where b is Wien's constant.
(Rσ)1/4⋅λmax=b
λmax=b⋅σ1/4R1/4
Thus, the wavelength at which the power radiated by the black body is maximum is given by:
λmax=b⋅σ1/4R1/4
After analyzing the options provided in the question, we can conclude that option D is the correct answer.
Similar Questions
The surface temperature of a hot body is 1227∘C. Find the wavelength at which it radiates maximum energy. Given Wien's constant = 0.2892 cm.K.
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
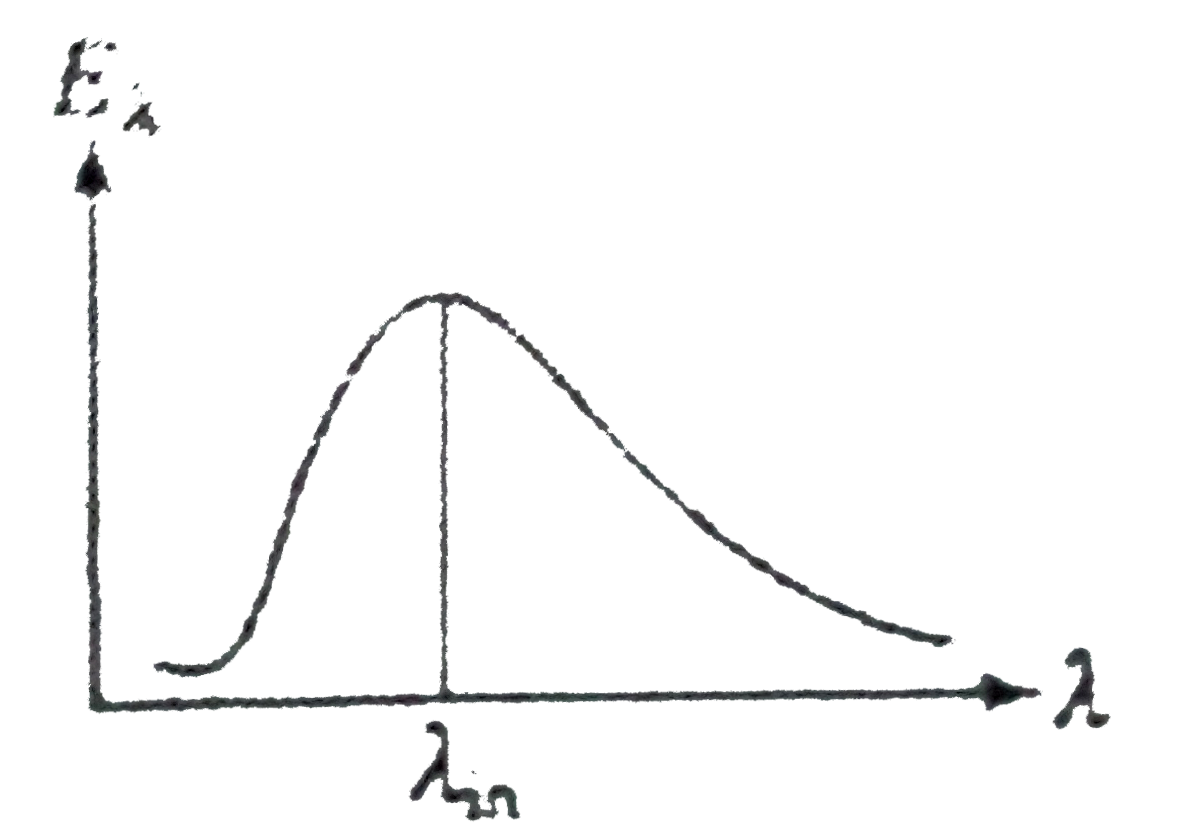
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
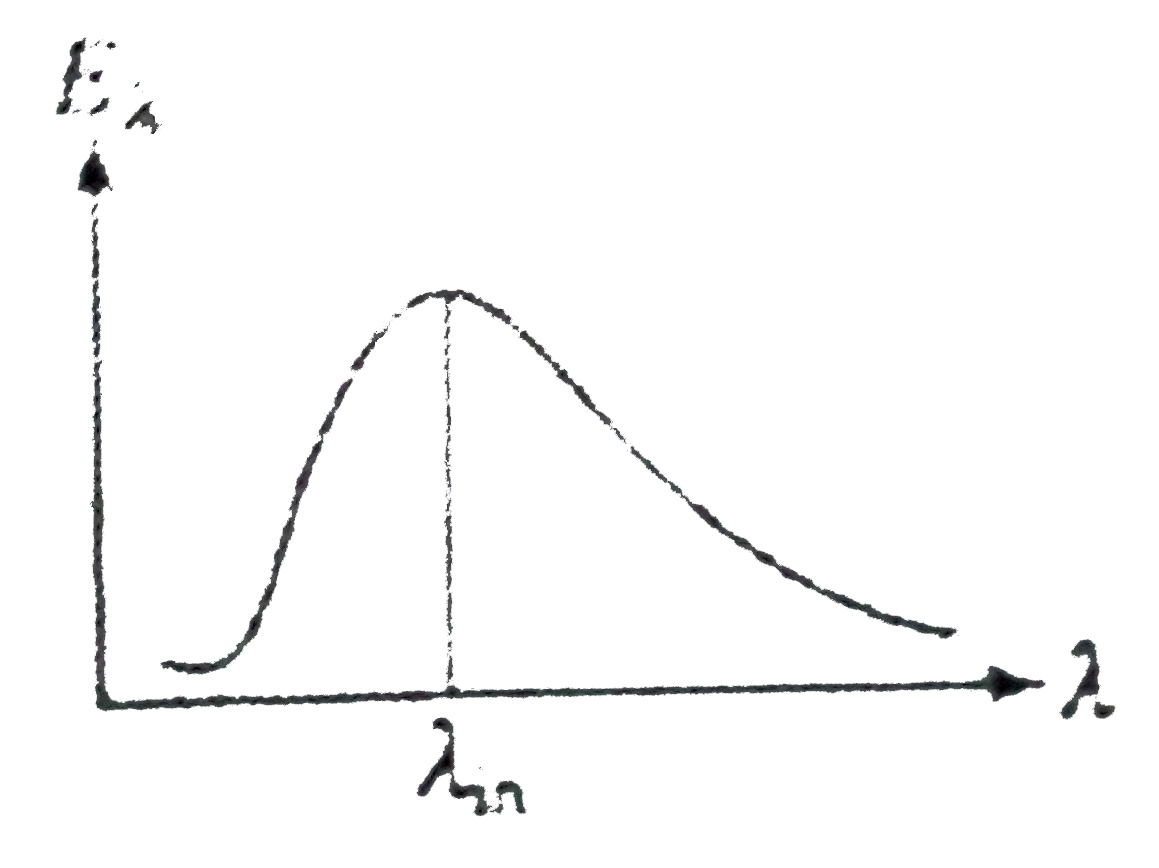
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?
View SolutionCalculate the wavelength at which a hot body radiates maximum energy if its surface temperature is 3200∘C. Wien's constant 0.00289 mK.
View SolutionA spherical black body of radius n radiates power p and its rate of cooling is R. then.
View SolutionIf λm denotes the wavelength at which the radiative emission from a black body at a temperature TK is maximum, then
View SolutionThe radiation emitted per unit time by unit area of a black body at temperature T is σT4 wehre σ is the Stefan-Boltzmann constant. The constant σ can also be expressed in terms of Boltmann's constant (k), Planck's constant (h) and speed of light (3) as σ=Akαhβcγ where A,α,β and γ are dimensionless constants. The set (α,β,γ) is givne by
View SolutionThe power radiated by a blackbody is P at a certain temperature. If power radiated by this body becomes 116th the times. then wavelength corresponding to maximum intensity becomes
View SolutionStatement I: As the temperature of the black body increases, the wavelength at which the spectral intensity (Eλ) is maximum decreases.
Statement II: The wavelength at which the spectral intensity will be maximum for a black body is proportional to the fourth power of its absolute temperature.
View SolutionThe power radiated by a black body is P, and it radiates maximum energy around the wavelength λ0. If the temperature of the black body is now changed so that it radiates maximum energy around a wavelength 3λ0/4, the power radiated by it will increase by a factor of
View Solution

