Three particles (A, B, C) each of mass m are connected by three massless rods of length l. All three particles lie on a smooth horizontal plane. A particle of mass m moving along one of the rods with velocity V0 strikes on a particle and stops (as shown in the diagram). Tension in any of the rod just after the collision is
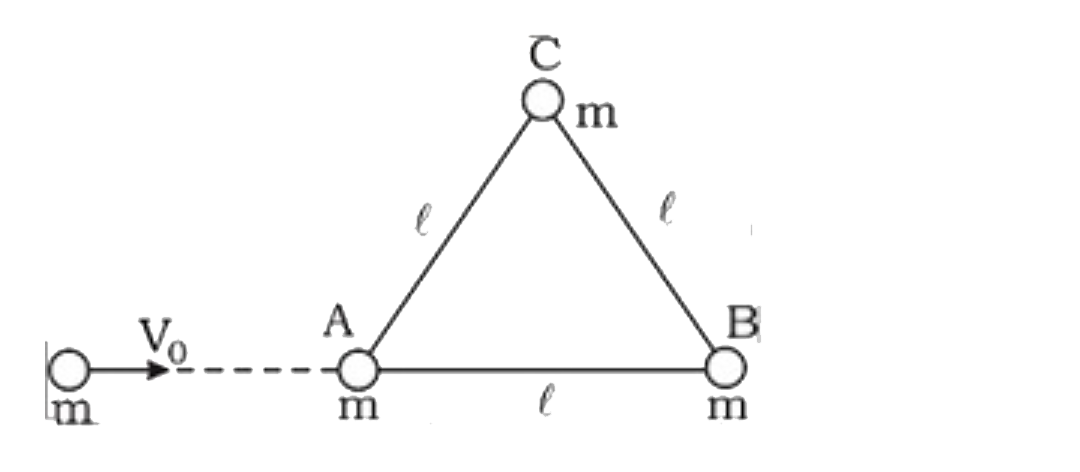
V0√3l
V0l
V02√2l
V03√3l
The correct Answer is:C
initial angular momentum=final angular momentum
L1=mv0l2√3=Icmω
mv0=l2√2=3m(l√3)2ω,ω=v02√3l
y=l2tan30∘=12√3
Similar Questions
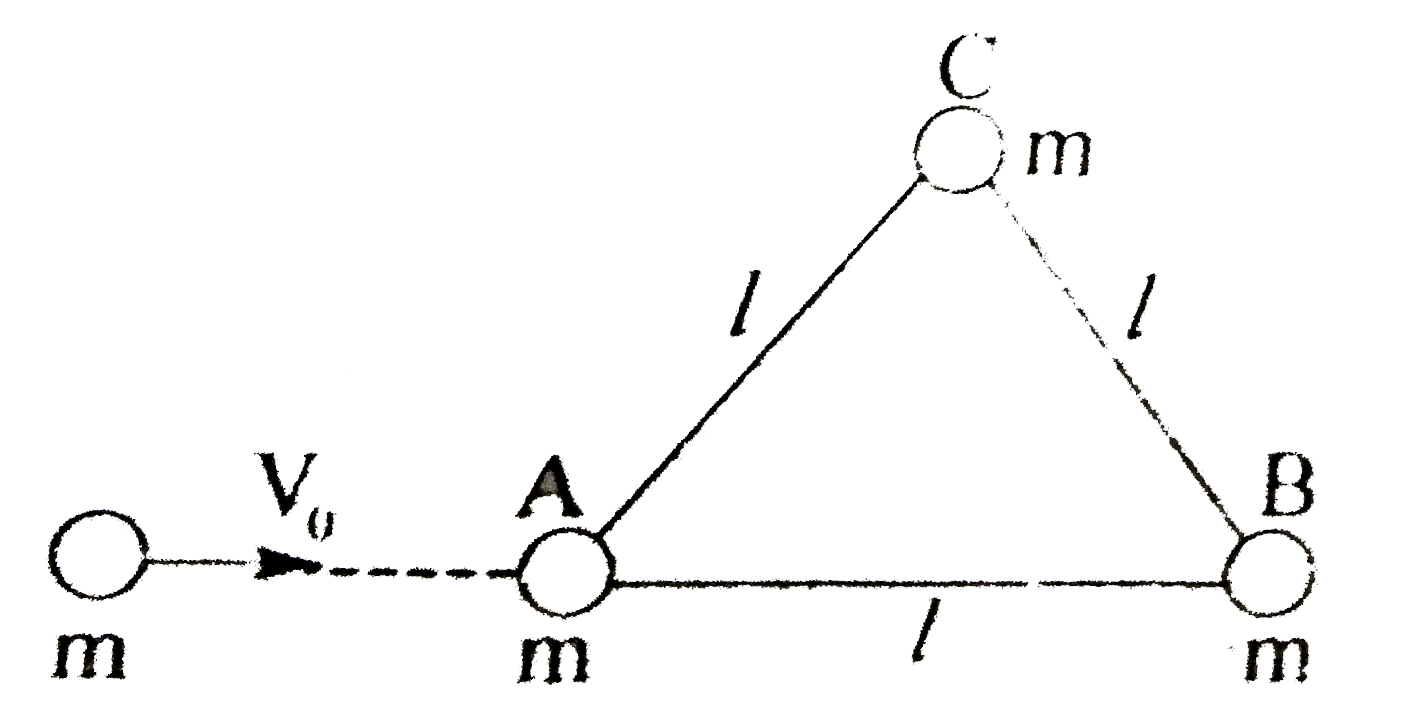
Three (A,B,C) particle each of mass m are connected by three mass-less rod of length l. All three particle lies on smooth horizontal plane. A particle of mass moving along one of the rod with velocity v0 strikes on a particle and stops as shown in diagram. Angular velocity of eachh particle after collision is.
View SolutionTwo particles each of mass M are connected by a massless rod. The rod is lying on the smooth horizontal surface. If one of the particle is given an impulse MV as shown in the figure then angular velocity of the system would be:

View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
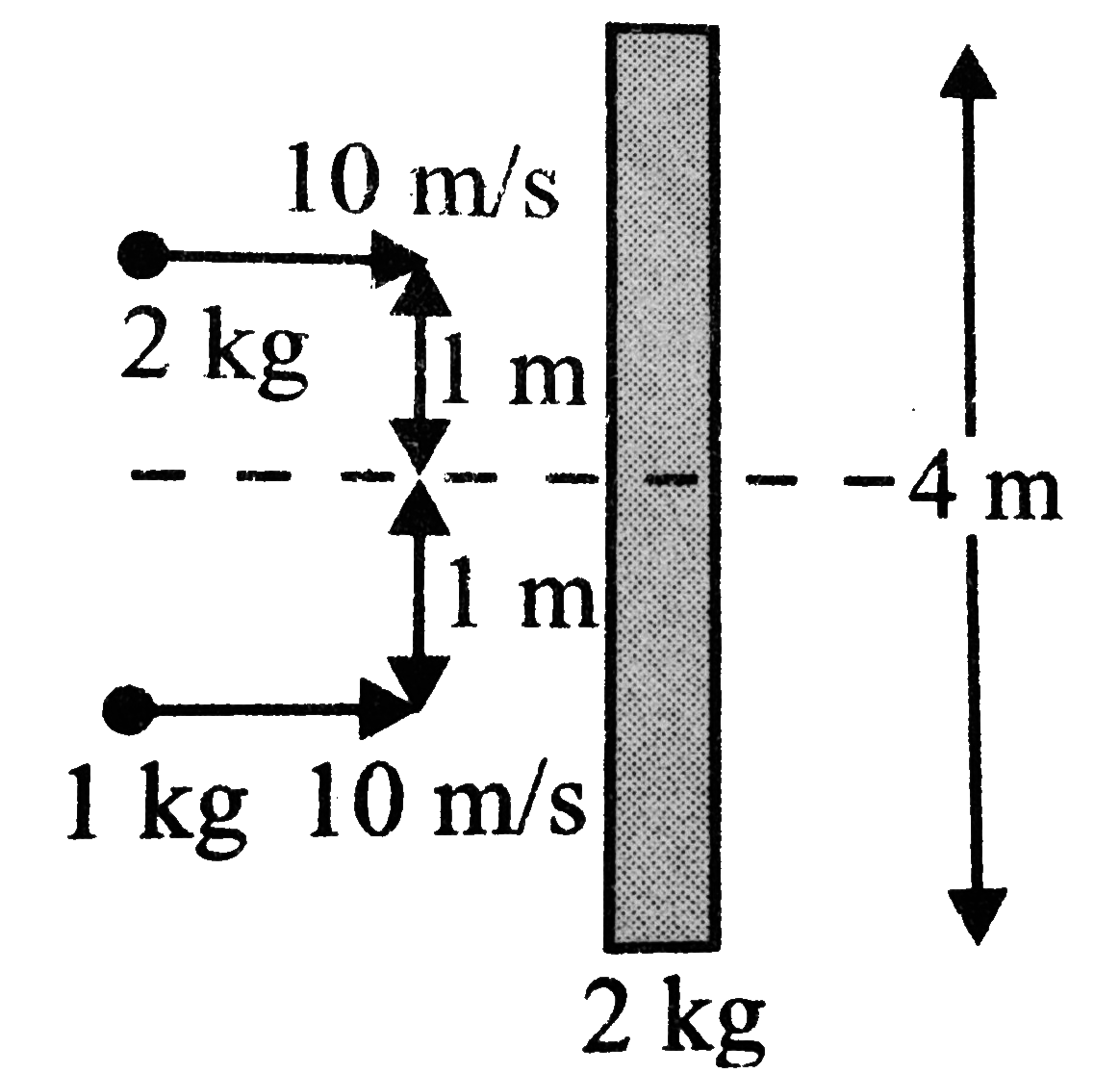
Velocity of the centre of mass of the rod after collision is
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
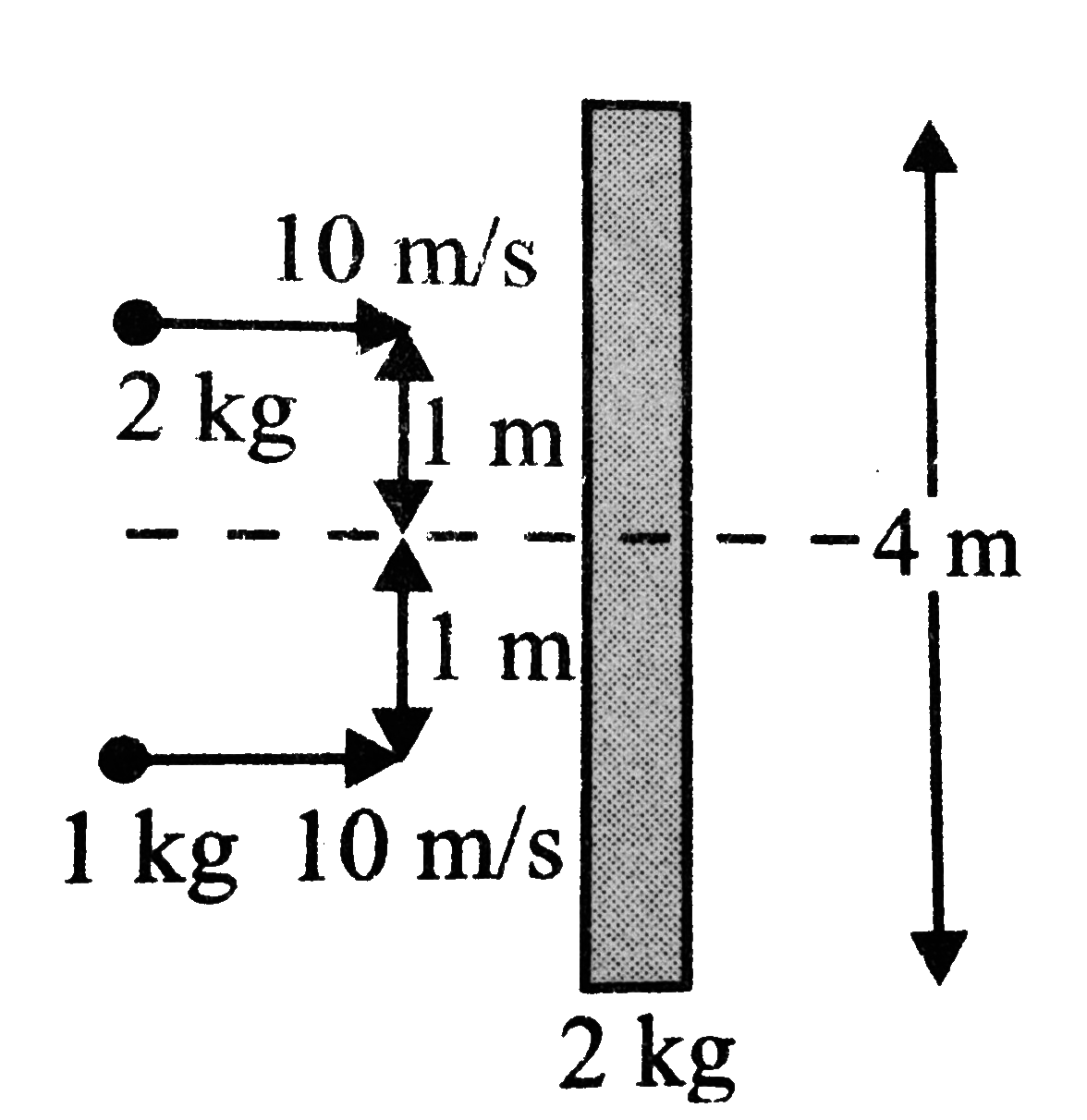
Angular velocity of the rod after collision is
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of mass 2kg and length 1m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2ms−1 perpendicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionA uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
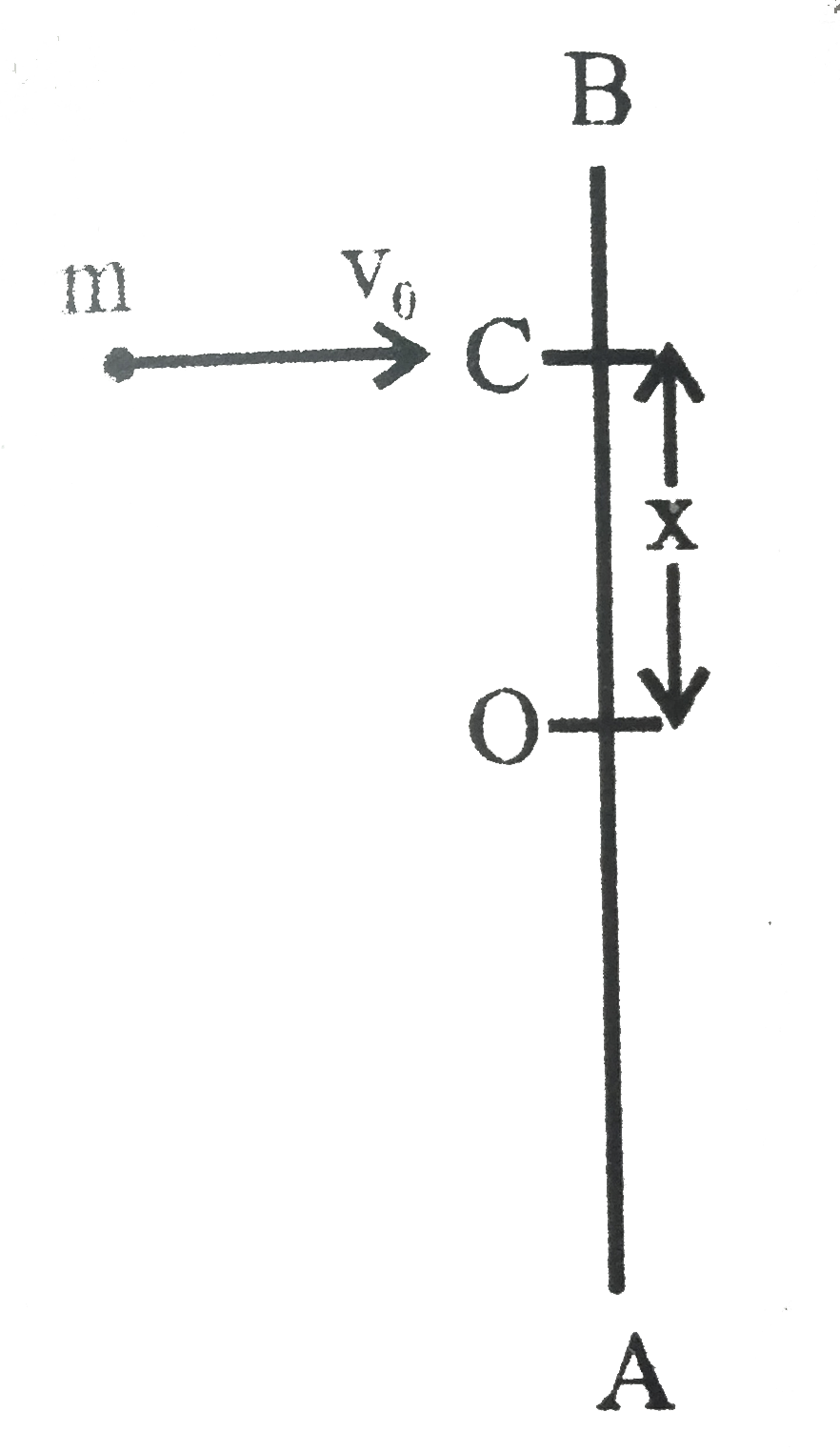 .
.
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View Solution
