Which of the following is a graph of the relation of the density (ρ) of a gas sample to the absolute tempeature keeping constant pressure.
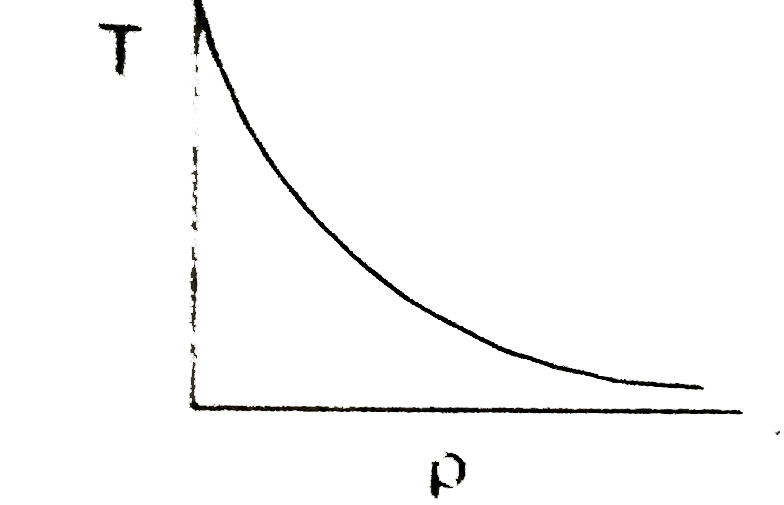


The correct Answer is:A
To solve the question regarding the relationship between the density (ρ) of a gas sample and the absolute temperature (T) while keeping the pressure constant, we can follow these steps:
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure
- V = Volume
- n = Number of moles
- R = Universal gas constant
- T = Absolute temperature
Step 2: Relate Density to Volume
Density (ρ) is defined as:
ρ=mV
Where:
- m = Mass of the gas
- V = Volume of the gas
We can express the volume in terms of density:
V=mρ
Step 3: Substitute Volume in the Ideal Gas Law
Substituting the expression for volume into the ideal gas law gives:
P(mρ)=nRT
Step 4: Express Moles in Terms of Density
The number of moles n can be expressed as:
n=mM
Where M is the molar mass of the gas. Substituting this into the equation gives:
P(mρ)=(mM)RT
Step 5: Simplify the Equation
Cancelling m from both sides (assuming m≠0):
Pρ=RTM
Step 6: Rearranging the Equation
Rearranging the equation gives:
ρ=PMRT
Step 7: Analyze the Relationship
From the equation ρ=PMRT, we can see that:
- When pressure P and molar mass M are constant, density ρ is inversely proportional to temperature T.
- This means that as temperature increases, density decreases, and vice versa.
Step 8: Determine the Graph
The relationship ρ∝1T indicates that the graph of density versus temperature will be a hyperbola that decreases as temperature increases. Therefore, the correct graph will show a decrease in density with an increase in temperature.
Conclusion
The correct answer to the question is option A, which reflects the inverse relationship between density and temperature at constant pressure.
---
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure
- V = Volume
- n = Number of moles
- R = Universal gas constant
- T = Absolute temperature
Density (ρ) is defined as:
ρ=mV
Where:
- m = Mass of the gas
- V = Volume of the gas
V=mρ
Substituting the expression for volume into the ideal gas law gives:
P(mρ)=nRT
The number of moles n can be expressed as:
n=mM
Where M is the molar mass of the gas. Substituting this into the equation gives:
P(mρ)=(mM)RT
Cancelling m from both sides (assuming m≠0):
Pρ=RTM
Rearranging the equation gives:
ρ=PMRT
From the equation ρ=PMRT, we can see that:
- When pressure P and molar mass M are constant, density ρ is inversely proportional to temperature T.
- This means that as temperature increases, density decreases, and vice versa.
The relationship ρ∝1T indicates that the graph of density versus temperature will be a hyperbola that decreases as temperature increases. Therefore, the correct graph will show a decrease in density with an increase in temperature.
The correct answer to the question is option A, which reflects the inverse relationship between density and temperature at constant pressure.
Similar Questions
Which of the following graph represents the variation of amount of chemisorption of a gas by a solid with temperature under constant pressure?
View SolutionWhich of the following shown the correct relationship between the pressure 'P' and density ρ of an ideal gas at constant temperature?
View SolutionHeat supplied to an ideal gas sample at constant Pressure :
View SolutionWhich graph correctly represents variation between relaxation time (t) of gas molecules with absolute temperature of gas T.
View SolutionWhich graph correctly represents variation between relaxation time (t) of gas molecules with absolute temperature of gas T.
View Solutionwhich one of the following graph is not correct for ideal gas ?

d=density ,P=pressure,T=Temperature
View SolutionFrom the graph the order of pressure of a gas is
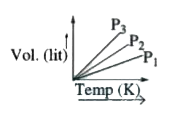
View SolutionWhen the pressure of a gas is doubled under constant temperature the density becomes
View SolutionWrite down the relation connecting the pressure and temperature of a gas if volume is kept constant.
View SolutionWhich of the following graphs is inconsistent with ideal gas behaviour ? (Assume n = constant)
View Solution