Listed in the table are forward and reverse rate constants for the reaction
Select the correct statement
Reaction is exothermic and value of equilibrium constant at 1400 K is
Reaction is endothermic and value of equilibrium constant at 1400 K is
Reaction is exothermic and value of at 1400 K is
Reaction is endothermica and value of at 1500 K is
The correct Answer is:C
at 1400 K
at
Since, decreases on increasing temperature So reaction is exothermic
Similar Questions
Knowledge Check
The rate constant for the reaction, 2N2O5→4NO2+O2 is 3.0×10−5s−1. If the rate is 2.40×10−5molL−1s−1, then the initial concentration of N2O5 (in molL−1) is
A0.8B0.7C1.2D1
The kinetic date for the given reaction A(g)+2B(g)K−−→C(g) is provided in the following table for three experiments at 300 K
Ex. No.[A/M][B/M]Initial rate(Msec−1)1.0.010.016.930×10−62.0.020.011.386×10−53.0.20.021.386×10−5
In another experiment starting swith initial concentration of 0.5 and 1 M respectively for A and B at 300 K, find the rate of reaction after 50 minutes from the starting of edperiment (inM/sec).
View SolutionThe equilibrium constant for the reaction
N2(g)+O2(g)⇔2NO(g)
at temperature T is 4×10−4.
The value of Kc for the reaction
NO(g)⇔12N2(g)+12O2(g)
at the same temperature is
View SolutionThe equilibrium constant for the reaction
N2(g)+O2(g)⇔2NO(g)
at temperature T is 4×10−4.
The value of Kc for the reaction
NO(g)⇔12N2(g)+12O2(g)
at the same temperature is
View SolutionThe equilibrium constant for the reaction
N2(g)+O2(g)⇔2NO(g)
at temperature T is 4×10−4.
The value of Kc for the reaction
NO(g)⇔12N2(g)+12O2(g)
at the same temperature is
View SolutionThe equilibrium constant for the reaction
N2(g)+O2(g)⇔2NO(g)
at temperature T is 4×10−4.
The value of Kc for the reaction
NO(g)⇔12N2(g)+12O2(g)
at the same temperature is
View SolutionThe equilibrium constant for the given reaction:
SO3(g)⇔SO2(g)+1/2O2(g), (Kc=4.9×10−2)
The value of Kc for the reaction:
2SO2(g)+O2(g)⇔2SO3(g), will be :
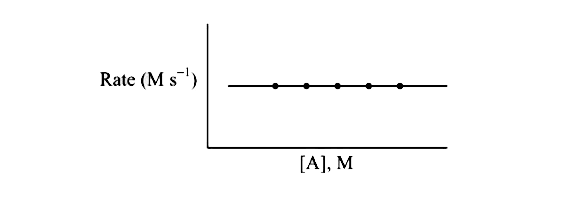
View SolutionFollowing reaction can take place in both direction Ak1k2B. For the forward reaction and for the backward direction
[B]Rate0.01M1×10−2Ms−10.02M2×10−2Ms−1
Hence, net reaction rate is :
View Solution