If uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -
zero
−5E0x0
−3E0x0
−√5E0x0
The correct Answer is:B
To solve the problem, we need to find the electric potential at the point (x0,2x0) given the uniform electric field →E=E0^i+2E0^j and that the potential V at the point (0,0) is zero.
1. Understand the Electric Field and Potential Relation:
The potential difference ΔV between two points in an electric field is given by:
ΔV=V(B)−V(A)=−∫BA→E⋅d→r
where A is the starting point and B is the ending point.
2. Identify the Points:
Let point A be (0,0) and point B be (x0,2x0). The potential at point A is given as V(0,0)=0.
3. Set Up the Integral:
The differential displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
The electric field →E is given as:
→E=E0^i+2E0^j
4. Calculate the Dot Product:
The dot product →E⋅d→r is:
→E⋅d→r=(E0^i+2E0^j)⋅(dx^i+dy^j)=E0dx+2E0dy
5. Set Up the Integral for Potential:
The potential at point B can be calculated as:
V(x0,2x0)=V(0,0)−∫(x0,2x0)(0,0)→E⋅d→r
Since V(0,0)=0, we have:
V(x0,2x0)=−∫x00E0dx−∫2x002E0dy
6. Evaluate the Integrals:
- For the first integral:
−∫x00E0dx=−E0(x)x00=−E0x0
- For the second integral:
−∫2x002E0dy=−2E0(y)2x00=−2E0(2x0)=−4E0x0
7. Combine the Results:
Now, adding both contributions:
V(x0,2x0)=−E0x0−4E0x0=−5E0x0
Final Result:
Thus, the potential at the point (x0,2x0) is:
V(x0,2x0)=−5E0x0
The potential difference ΔV between two points in an electric field is given by:
ΔV=V(B)−V(A)=−∫BA→E⋅d→r
where A is the starting point and B is the ending point.
Let point A be (0,0) and point B be (x0,2x0). The potential at point A is given as V(0,0)=0.
The differential displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
The electric field →E is given as:
→E=E0^i+2E0^j
The dot product →E⋅d→r is:
→E⋅d→r=(E0^i+2E0^j)⋅(dx^i+dy^j)=E0dx+2E0dy
The potential at point B can be calculated as:
V(x0,2x0)=V(0,0)−∫(x0,2x0)(0,0)→E⋅d→r
Since V(0,0)=0, we have:
V(x0,2x0)=−∫x00E0dx−∫2x002E0dy
- For the first integral:
−∫x00E0dx=−E0(x)x00=−E0x0
- For the second integral:
−∫2x002E0dy=−2E0(y)2x00=−2E0(2x0)=−4E0x0
Now, adding both contributions:
V(x0,2x0)=−E0x0−4E0x0=−5E0x0
Thus, the potential at the point (x0,2x0) is:
V(x0,2x0)=−5E0x0
Topper's Solved these Questions
Similar Questions
If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionThe electric field and the electric potential at a point are E and V respectively.
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
View SolutionConisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
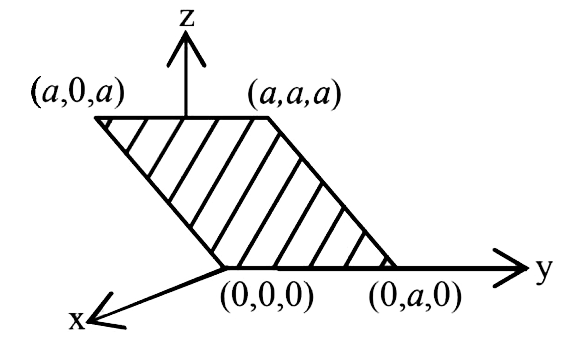
View SolutionAn electric field →E=20yˆj exist in space . The potential at (5 m, 5 m) is taken to be zero. The potential at origin is
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
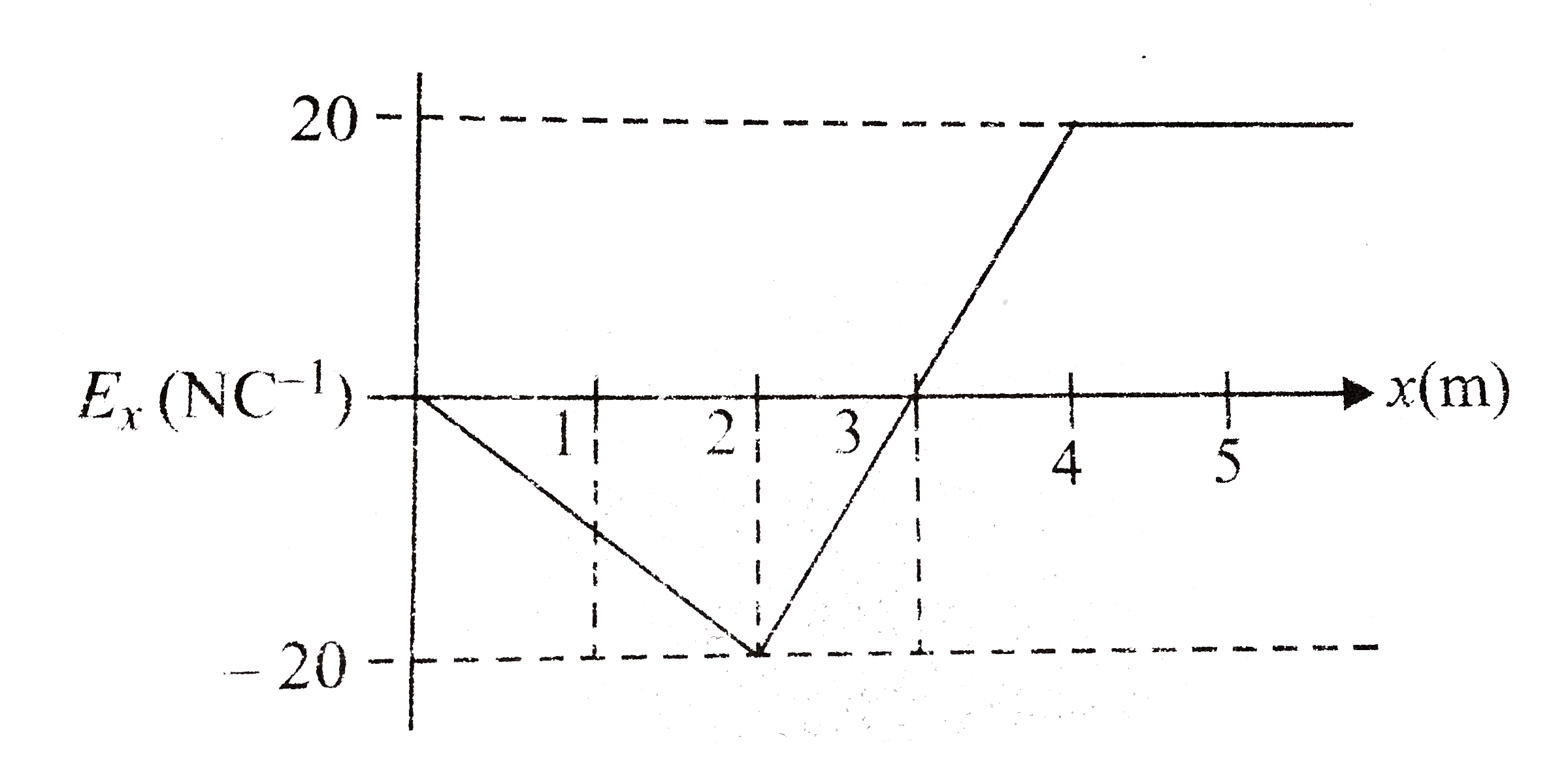
View SolutionIn certain region of space with volume 0.2 m3 the electric potential is found to be 5V throughout. The magnitude of electric field is this region is
View Solution

