In a standing wave on a string.
In one time period all the particles are simultaneously at rest once
All the particles must be at their positive extremes once in a time period
All the particles may be at their positive extremes simulanecously once in a time period.
All the particles are never at rest
The correct Answer is:B
Step by step video & image solution for In a standing wave on a string. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Superposition of waves interfarence, beats)
Explore 15 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
Statement I : In a standing wave on a string , the spacing between nodes is Δx. If the tension in string is increased wave same as before , then the separation between nearest nodes will be increased.
Statement II : Spacing between nodes ( consecutive) in the standing wave is equal to half of the wavelength of component waves.
View SolutionLet the two waves y1=Asin(kx−ωt) and y2=Asin(kx+ωt) from a standing wave on a string . Now if an additional phase difference of ϕ is created between two waves , then
View SolutionStatement I : In standing waves on a string , the medium particles , i.e., different striung elements remain at rest .
Statement II : In standing waves all the medium particles attain maximum velocity twice in one cycle.
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.
View SolutionExplain the formation of standing waves in a string clamped at both ends and discuss the various modes of vibration.
View SolutionThe equation of a standing wave in a string fixed at both its ends is given as y=2A sin kx cos ωt. The amplitude and frequency of a particle vibrating at the point of string midway between a node and an antinode is
View SolutionThe wave-function for a certain standing wave on a string fixed at both ends is y(x,t)=0.5sin(0.025πx)cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :
View SolutionThe vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be 400m/s for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View SolutionColumn I shows different sets of standing waves in a string of length L whose ends are fixed or free according to respective figure and Column - II shows possible equations for them where symbols have usual meaning
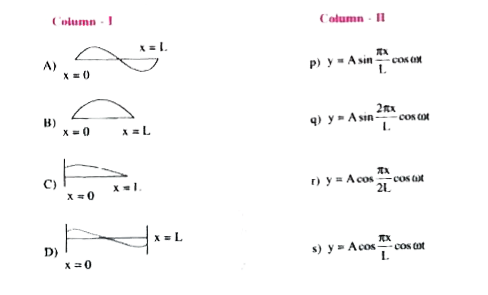
View SolutionA standing wave on a string is given by y=(4cm)cos[xπ]sin[50πt], where x is in metres and t is in seconds. The velocity of the string section at x=1/3matt=1/5s, is
View Solution

