A particle P is moving in a circle of radius 'a' with a uniform speed v. C is the centre of the circle and AB is a diameter. When passing through B the angular velocity of P about A and C are in the ratio
1:1
1:2
2:1
4:1
The correct Answer is:B
To solve the problem, we need to find the ratio of the angular velocities of a particle P moving in a circle about two points: A (one end of the diameter) and C (the center of the circle).
1. Identify the Parameters:
- Let the radius of the circle be a.
- The diameter AB is 2a.
- The speed of the particle P is v.
2. Determine the Angular Velocity about Point C:
- The angular velocity ωC about the center C can be calculated using the formula:
ωC=vr
- Here, r is the radius of the circle, which is a.
- Therefore, we have:
ωC=va
3. Determine the Angular Velocity about Point A:
- The distance from point A to point P when P is at point B is the diameter of the circle, which is 2a.
- The angular velocity ωA about point A is given by:
ωA=vR
- Here, R is the distance from A to P, which is 2a.
- Thus, we have:
ωA=v2a
4. Calculate the Ratio of Angular Velocities:
- Now, we can find the ratio of the angular velocities ωAωC:
ωAωC=v2ava=v2a⋅av=12
5. Final Result:
- Therefore, the ratio of the angular velocities of particle P about points A and C is:
ωA:ωC=1:2
Conclusion:
The answer is 1:2.
---
- Let the radius of the circle be a.
- The diameter AB is 2a.
- The speed of the particle P is v.
- The angular velocity ωC about the center C can be calculated using the formula:
ωC=vr
- Here, r is the radius of the circle, which is a.
- Therefore, we have:
ωC=va
- The distance from point A to point P when P is at point B is the diameter of the circle, which is 2a.
- The angular velocity ωA about point A is given by:
ωA=vR
- Here, R is the distance from A to P, which is 2a.
- Thus, we have:
ωA=v2a
- Now, we can find the ratio of the angular velocities ωAωC:
ωAωC=v2ava=v2a⋅av=12
- Therefore, the ratio of the angular velocities of particle P about points A and C is:
ωA:ωC=1:2
The answer is 1:2.
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (COLLISION AND CENTRE OF MASS )
Explore 12 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (ROTATIONAL MOTION)
Explore 72 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (WORK POWER & ENERGY)
Explore 34 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
Knowledge Check
A particle 'P' is moving in a circle of radius 'a' with a uniform speed 'u' 'C' is the centre of the circle and AB is a diameter. The angular velocity of P about A and C are in the ratio
A1:1B1:2C2:1D4:1A particle is moving in a circle with uniform speed. IT has constant
AvelocityBAccelerationCkinetic energyDdisplacement
When a particle moves in a circle with a uniform speed
View SolutionA particle is moving in a circle with uniform speed v . In moving from a point to another diametrically opposite point
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
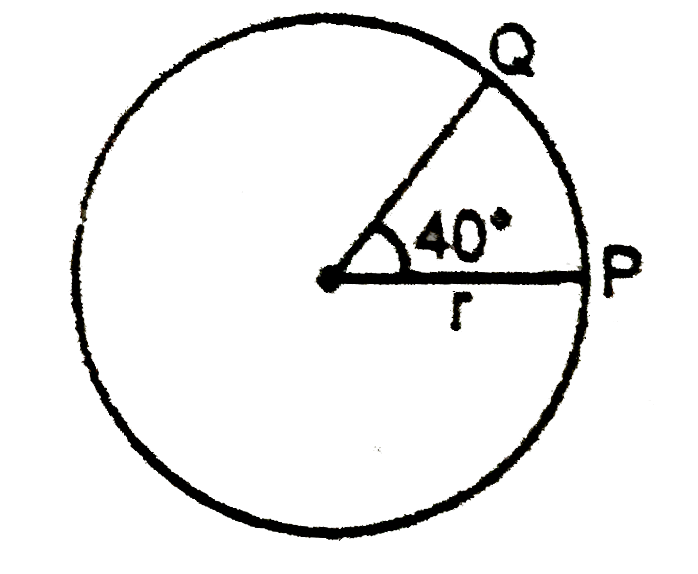
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
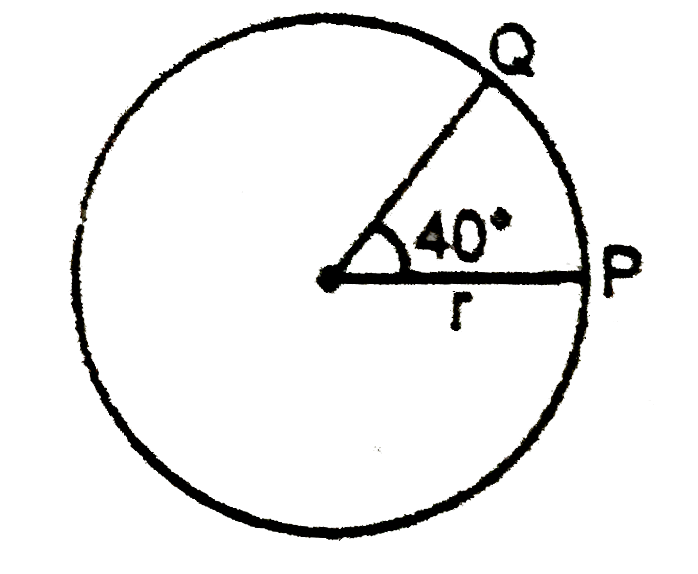
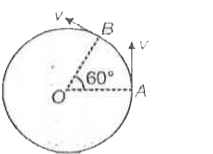
View SolutionA particle is moving in a circle of radius r having centre at O with a constant speed v . The magnitude of change in velocity in moving from A to B is
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View Solution

