A particle moves on straight line according to the velocity-time graph shown in fig. Calculate -
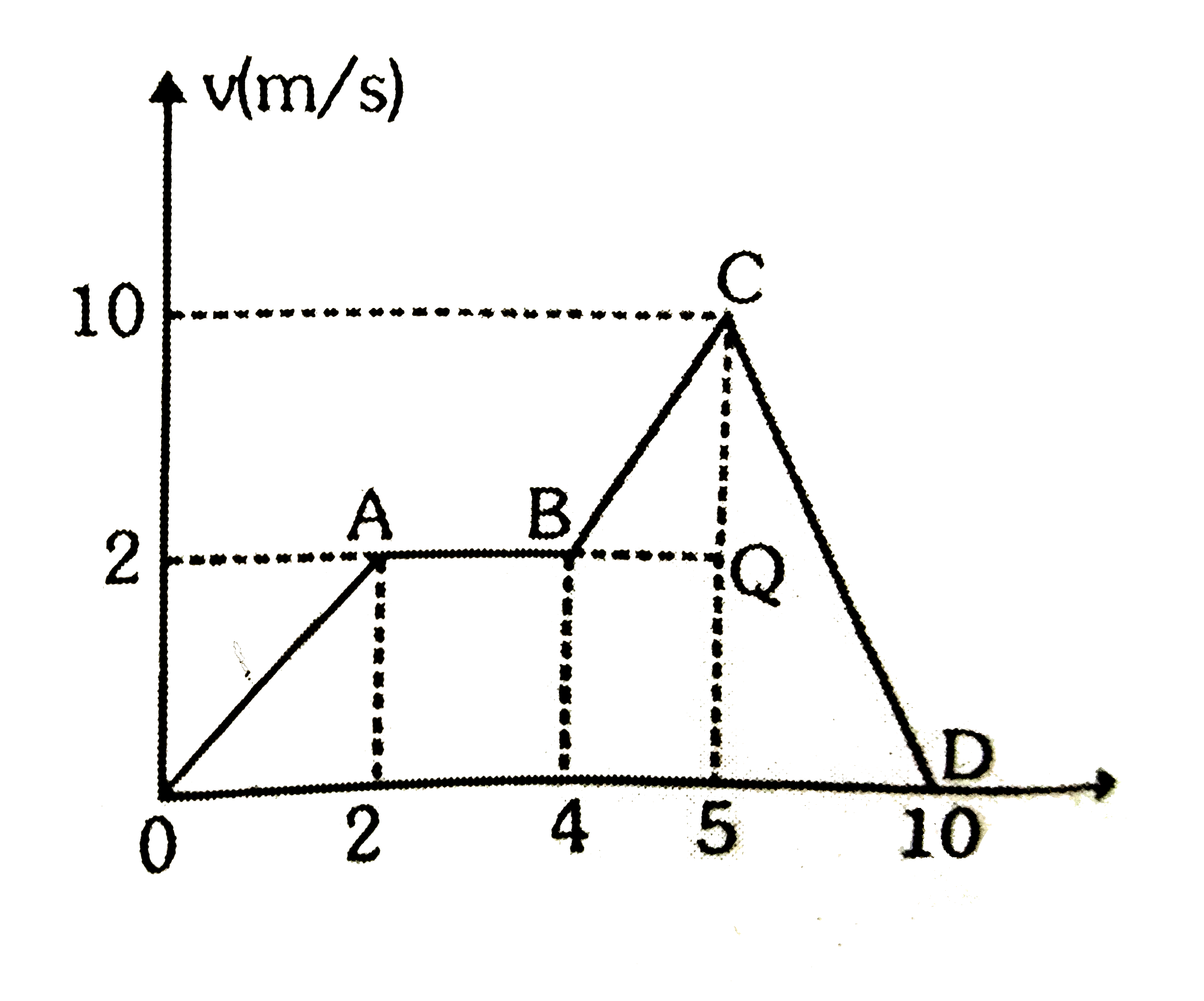
(i) Total distance covered
(ii) Average speed
(iii) In which part of the graph the acceleration is maximum and also find its value.
(iv) Retardation
(i) Total distance covered = Area under v - t curve
=12(2×2)+2(4−2)+12(10+2)×1
12×5×10=37 m
(ii) Average speed = Total distanceTotal time=3710=3.7m/s
(iii) Acceleration = Slope of v-t curve
So maximum acceleration will be in the part where the slope will be maximum i.e. BC
amax=aBC=10−21=8m/s2
(iv) Retardation = Slope of CD (As it is negative)
=∣∣∣0−105∣∣∣=|−2|=2m/s2
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-6
Explore 9 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-4
Explore 6 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-2
Explore 89 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Question
Explore 1 Video
Similar Questions
A particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
View Solutions-t graph of a particle in motion is shown in Fig. Calculate
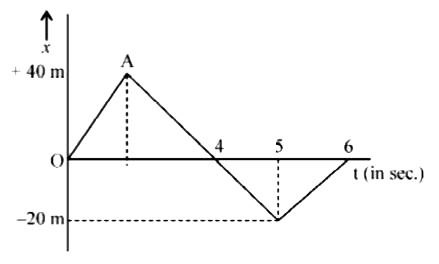
Total covered distance
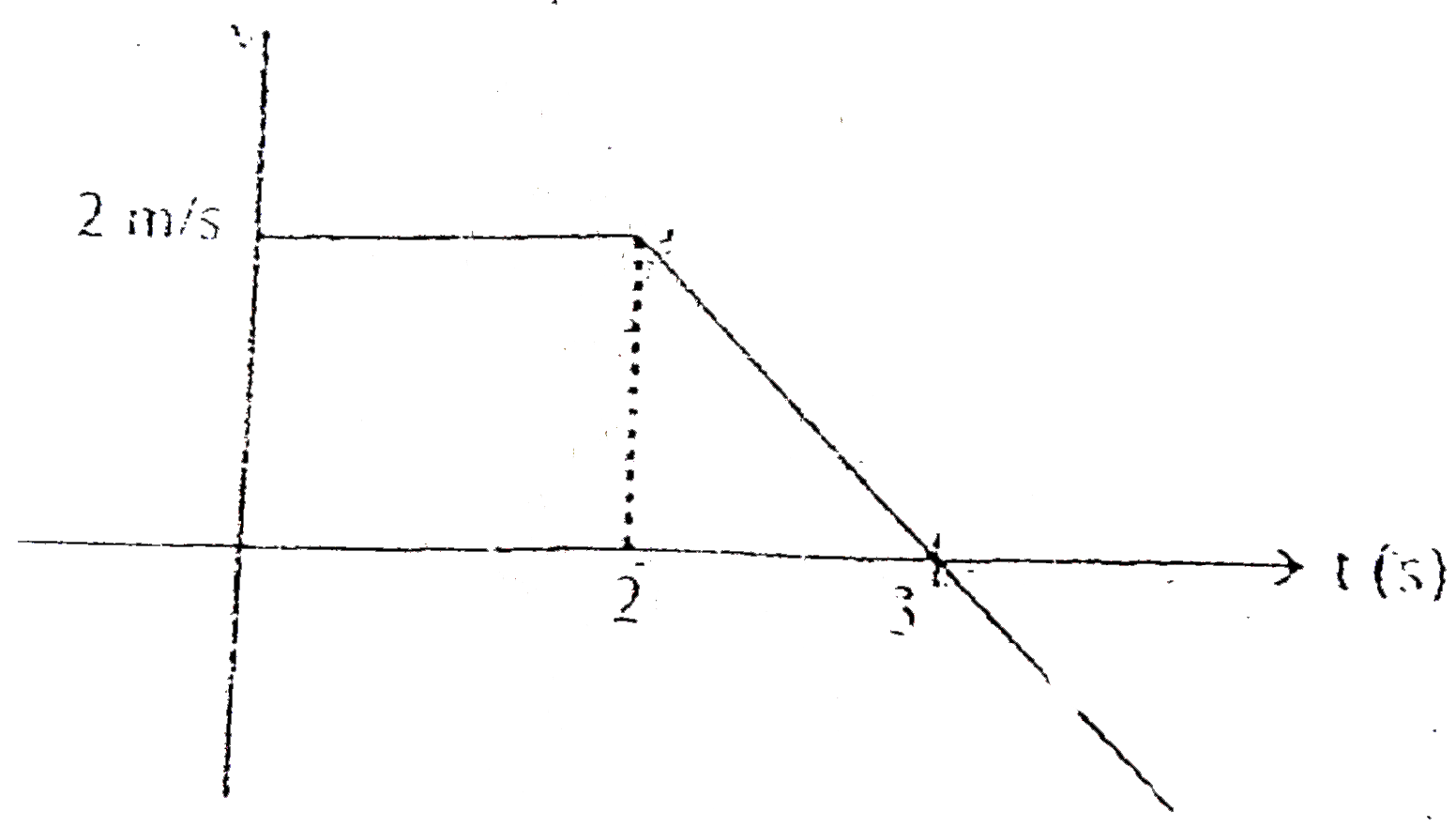
View SolutionA particle is moving on X−axis. Its velocity time graph is given in the figure. Find distance travelled by the particle in 5sec.
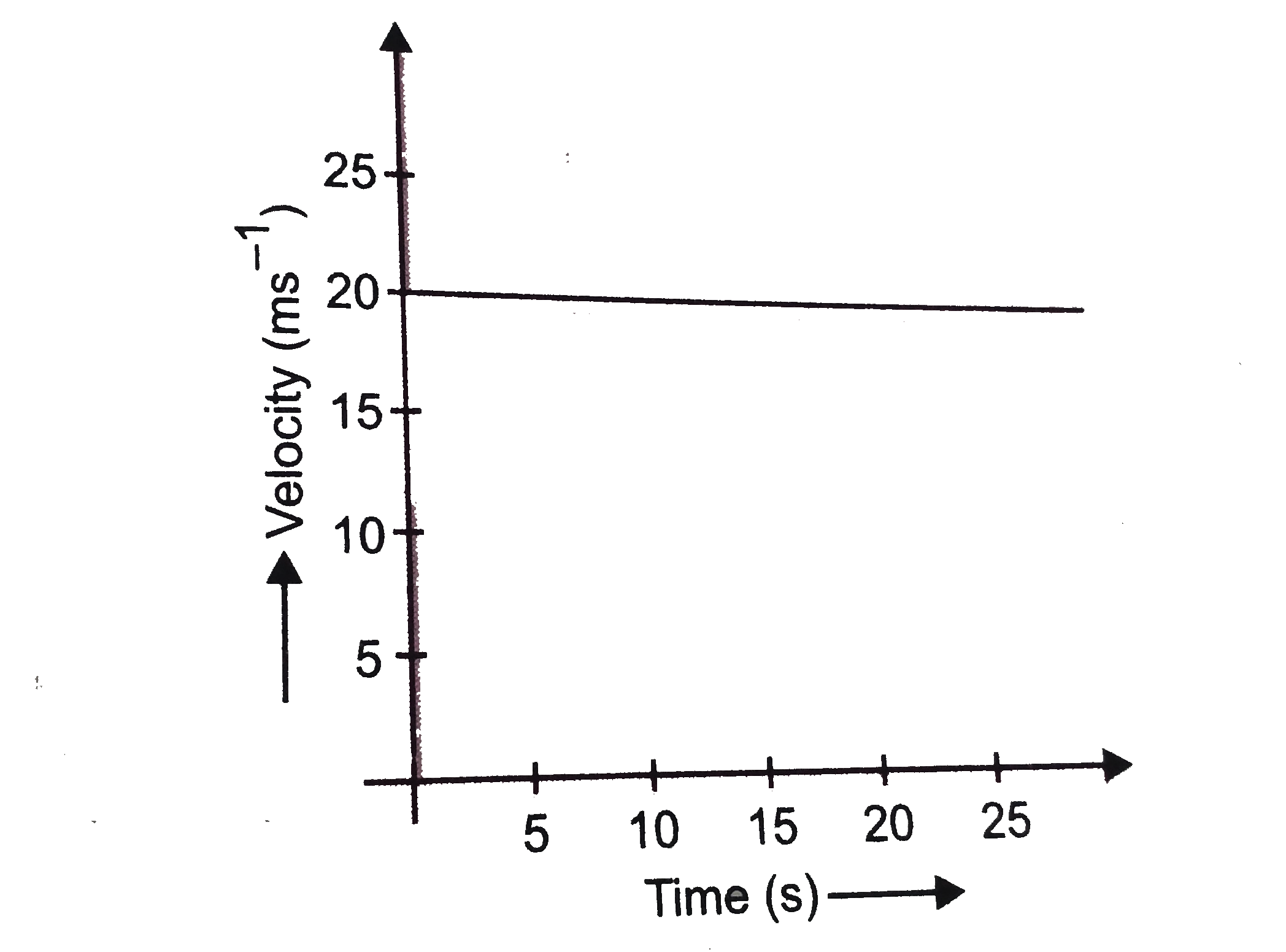
View SolutionThe velocity-time graph shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.
View SolutionA particle starts motion from rest and moves along a straight line. Its velocity-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionThe figure below shows the velocity-time graph of a body moving in a straight line.
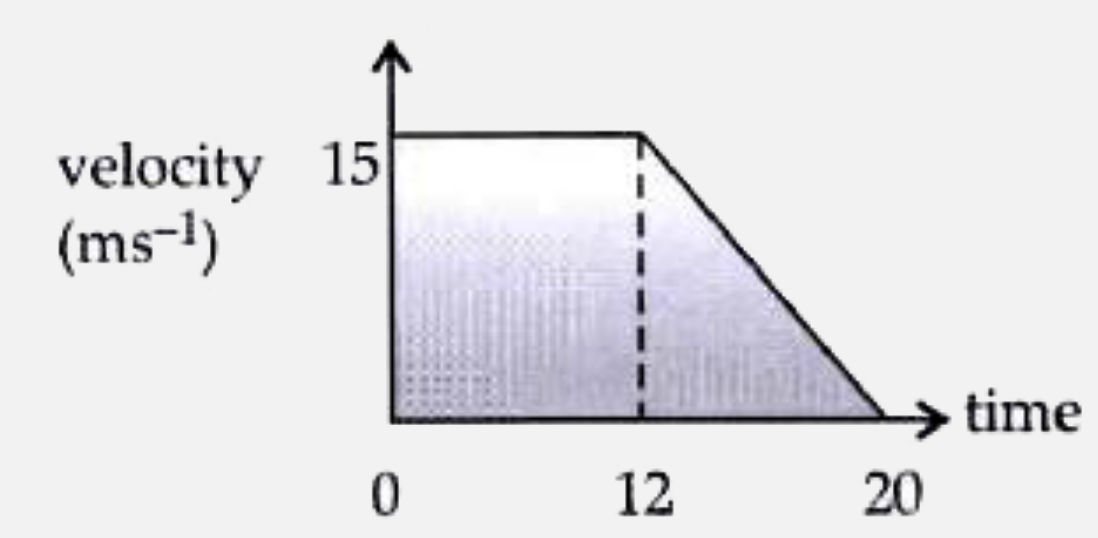
Find the time interval in which the body is moving with zero acceleration
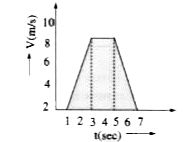
View SolutionFor the velocity - time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the total distance covered by it in all the seven seconds
View SolutionFrom the velocity-time plot shown in Fig. find the distance travelled by the particle during the first 40s. Also find the average velocity during this period.

View SolutionA particle starts to move along a straight line. The acceleration versus time graph of particle is as shown in figure. The correct velocity versus time graph is :

View Solution