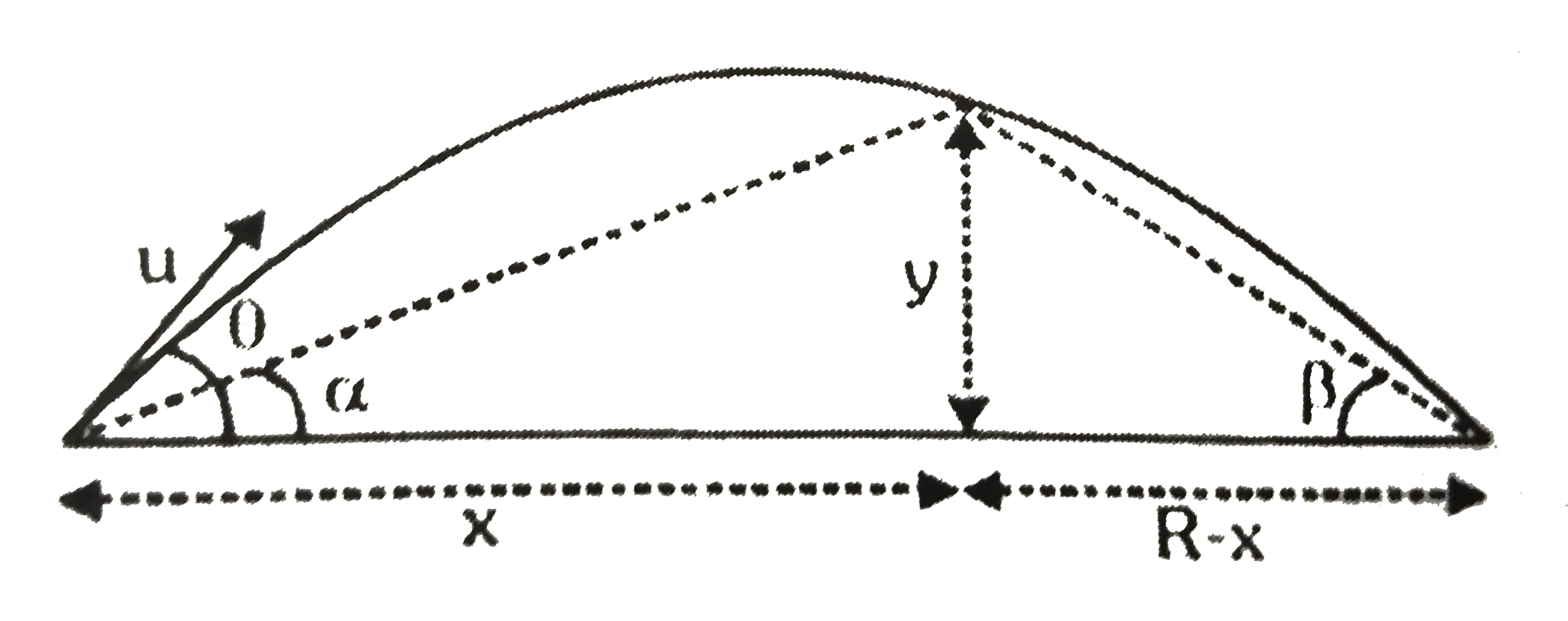
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
From triangle y=xtanαandy=(R−x)tanβ
tanα+tanβ=yx+yR−x=yRx(R−x)
∵y=xtanθ[1−xR]⇒tanθ=yRx(R−x)
∴tanθ=tanα+tanβ
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-1
6 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-2
7 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
Similar Questions
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
View SolutionIf cosθ=cosα−cosβ1−cosαcosβ,prove that tanθ2=±tanα2cotβ2.
View SolutionIf αandβ are roots of the equation acosθ+bsinθ=c, then find the value of tan(α+β).
View SolutionA shell fired from the base of a mountain just clears it. If α is the angle of projection, then the angular elevation of the summit β is
View SolutionIf α and β are acute such that α+β and α−β satisfy the equation tan2θ−4tanθ+1=0, then (α,β) =
View Solutionαandβ are acute angles and cos2α=3cos2β−13−cos2β then tanαcotβ=
View SolutionTwo particles are projected at the same instant from the same point at inclinations α and β to the horizontal. If they simultaneously hit the top and bottom of a vertical pole subtending angle θ at the point of projection , find (tanα−tanβ).
View SolutionIf tanβ=cosθtanα, then prove that tan2θ2=sin(α−β)sin(α+β).
View SolutionTwo parallel straight lines are inclined to the horizon at an angle ∝. A particle is projected from a point mid way between them so as to graze one of the lines and strikes the other at right angle. Show that if θ is the angle between the direction of projection and either of lines, then tanθ=(√2−1)cot∝.
View SolutionA train travelling on one of two intersecting railway lines, subtends at a certain station on the other line, an/ angle α when the front of the carriage reaches the junction and an angle β when the end of the carriage reaches it. Then, the two lines are inclined to each other at an angle θ, show that 2cotθ=cotα−cotβcotα+cotβ
View Solution
