On an open ground, a motorist follows a track that turns to his left by an angle of 60∘ after every 500m. Starting from a given turn, The path followed by the motorist is a regular hexagon with side 500m, as shown in the given figure specify the displacement of the motorist at the end of third turn
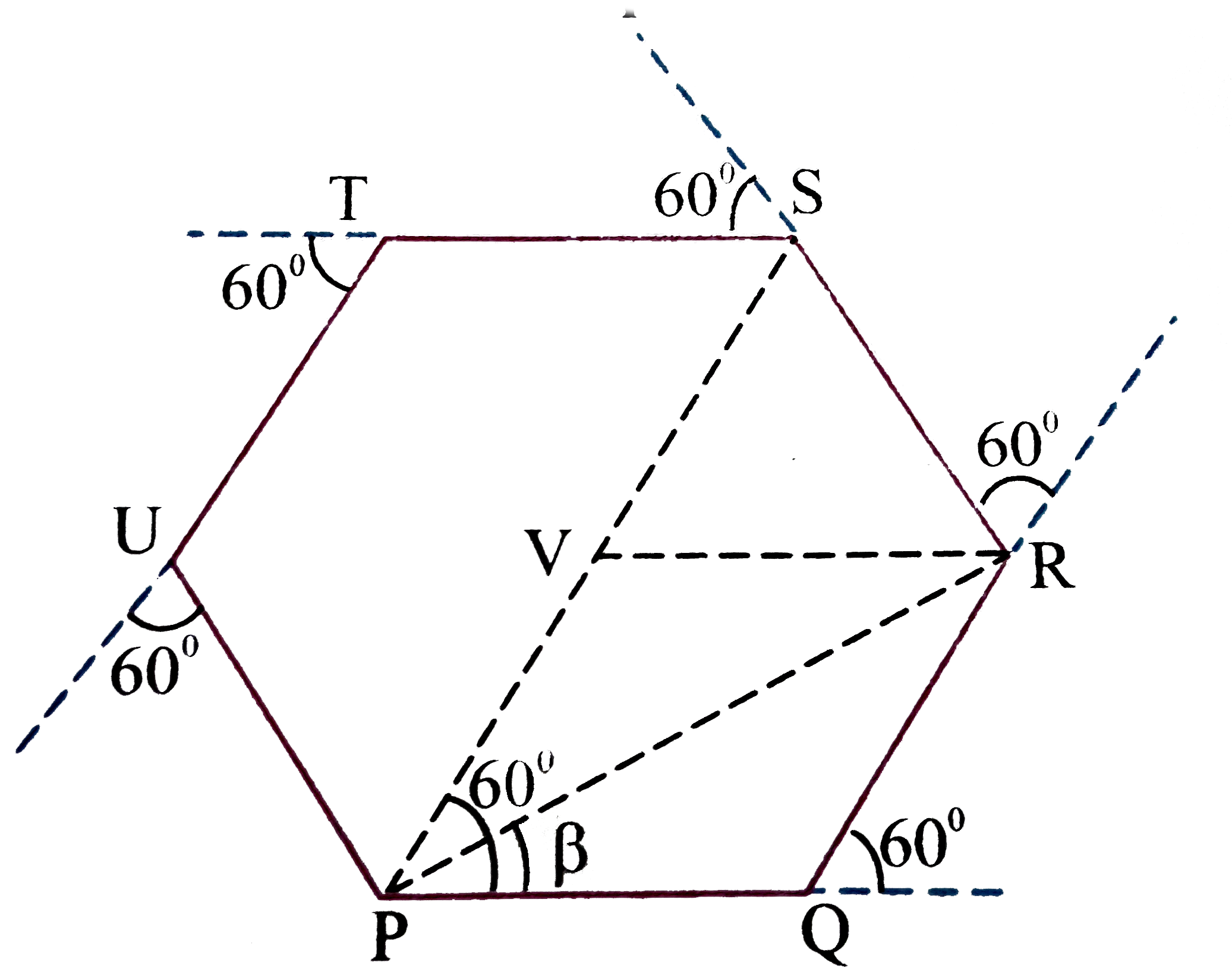
.
At III turn
|Displacement|=∣∣∣−−→OA+−−→AB+−−→BC∣∣∣=∣∣∣−−→OC∣∣∣
=500cos60∘+500+500cos60∘
=500×12+500+500×12=1000 m
So |Displacement| = 1000 m from O to C
Distance = 500 + 500 + 500 = 1500 m ∴|Displacement|Distance =10001500=23
At VI turn
∵ initial and final positions are same so |displacement| = 0 and distance = 500 × 6 = 3000 m
∴|Displacement|Distance=03000=0
At VIII turn
|Displacement|=2(500)cos(60∘2)=1000×cos30∘=1000×√32=500√3 m
Distance =500×8=4000 m ∴|Displacement|Distance=500√34000=√38
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-1
Explore 6 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-2
Explore 7 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-2
Explore 89 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Question
Explore 1 Video
Similar Questions
On an open ground, a motorist follows a track that turns to his left by an angle of 60∘ after every 500m. Starting from a given turn, The path followed by the motorist is a regular hexagon with side 500m, as shown in the given figure specify the displacement of the motorist

at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
View SolutionA person moving on a motor cycle in a ground takes a turn through 60∘ on his left after every 50m. Then find the magnitude of displacement suffered by him after 9th turn
View SolutionA man moves in an open field such that after moving 10 m on a straight line , he makes a sharp turn of 60∘ to his left. The total displacement just at the start of 8th turn is equal to
View SolutionA rod of length L and mass M is acted on by two unequal force F1andF2(<F1) as shown in the following figure.

The tension in the rod at a distance y from the end a is given by
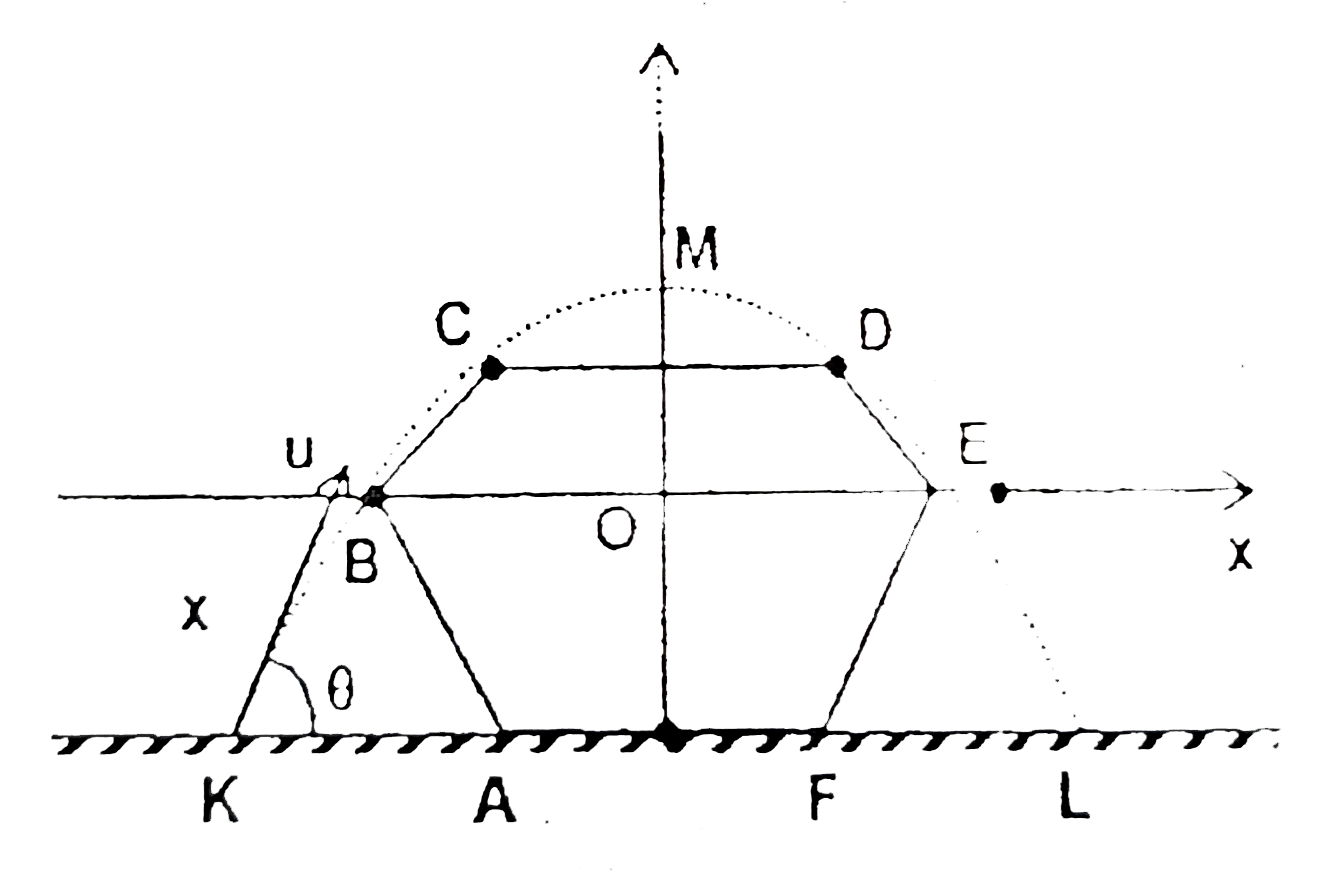
View SolutionA regular hexagon of side a=10√3m is kept at horizontal surface as shown in the figure. A particle is projected with velocity Vm/s at an angle θ from point K such that it will just touches the all four corners regular hexagon at B, C, D and E as shown in the figure. If O is the centre of hexagon and x−axis is parallel to horizontal and y−axis is perpendicular to AF and CD side of hexagon then answer the following [take g=10m/s2]
The maximum height from horizontal surface attained by projectile is

View SolutionA regular hexagon of side a=10√3m is kept at horizontal surface as shown in the figure. A particle is projected with velocity Vm/s at an angle θ from point K such that it will just touches the all four corners regular hexagon at B, C, D and E as shown in the figure. If O is the centre of hexagon and x−axis is parallel to horizontal and y−axis is perpendicular to AF and CD side of hexagon then answer the following [take g=10m/s2]
The time required to move the particle from D to E is
View SolutionFour girls skating on circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in figure. For which girls displacement is equal to the actual length of path ?
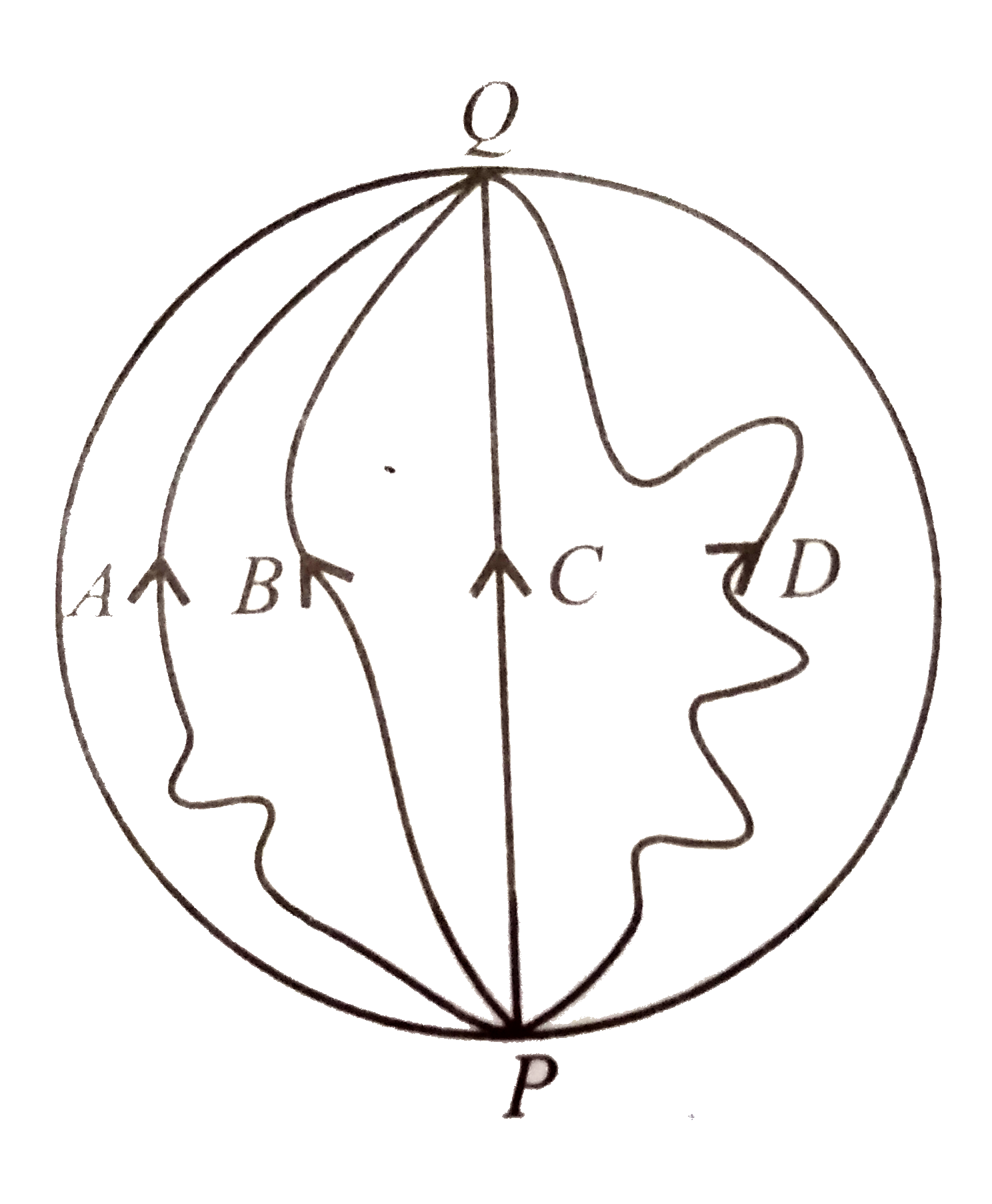
View SolutionThree girls skating on a circular ice ground of radius 200m start from a point (P) on the edge of the ground and reach a point Q diametrically opposite to (P) following different paths as shown in Fig. What is the magnitude of the displacement vector for each ? which girl's displacement is equal to the actual length of path skate ?
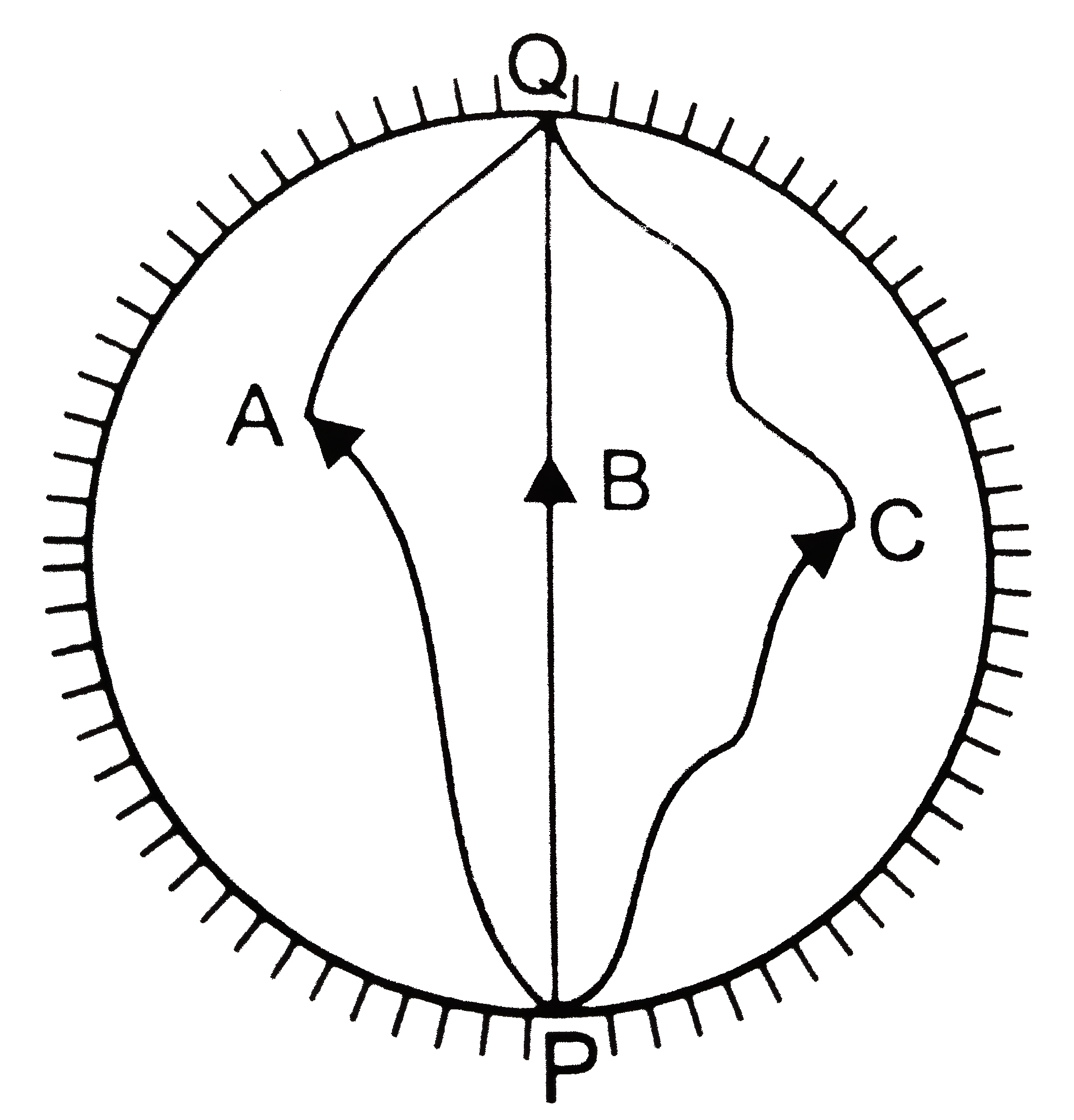 .
.
View SolutionThe work done in turning a magnet of magnetic moment 'M' by an angle of 90∘ from the meridian is 'n' times the corresponding work done to turn it through an angle of 60∘, where 'n' is given by
View SolutionThe work done in turning a magnet of magnetic moment 'M' by an angle of 90∘ from the meridian is 'n' times the corresponding work done to turn it through an angle of 60∘, where 'n' is given by
View Solution