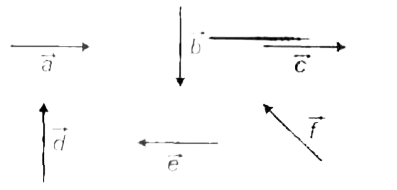
Six vector →a through →f have the magnitudes and direction indicated in the figure. Which of the following statements is true?

→b+→e=→f
→b+→c=→f
→d+→c=→f
→d+→e=→f
The correct Answer is:4
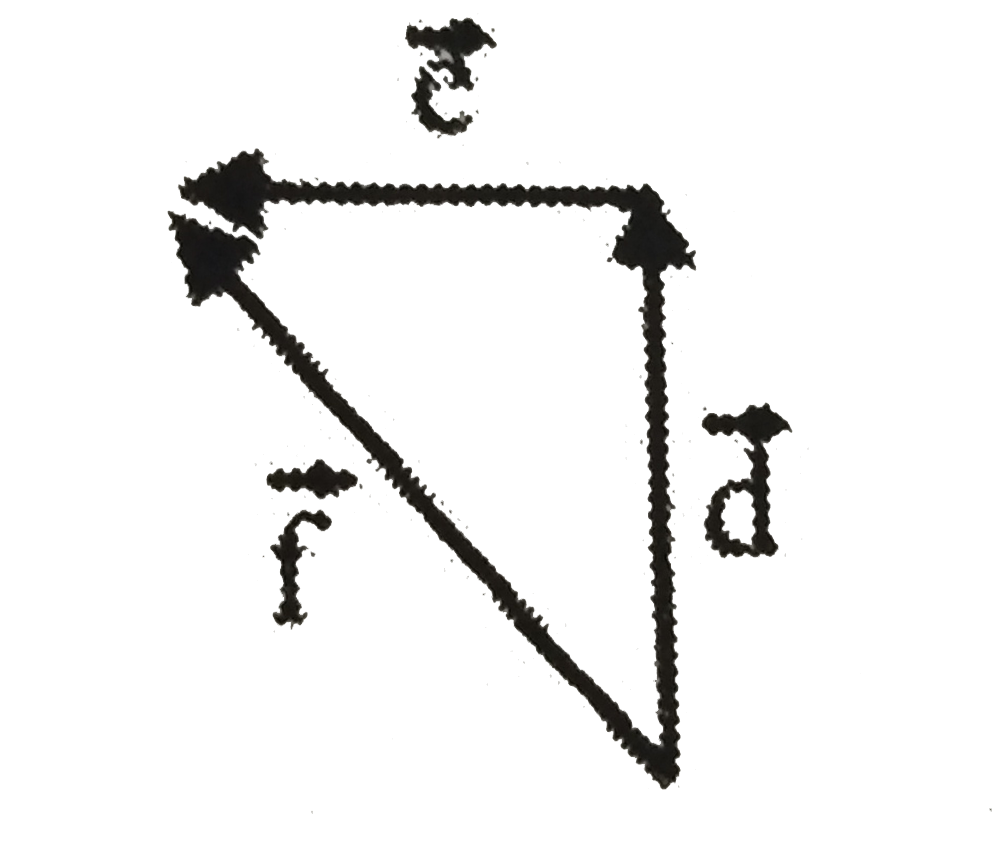
⇒→f=→d+→e
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-III CHECK YOUR UNDERSTANDING
15 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - CROSS PRODUCT
15 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
Knowledge Check
The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8
A particle performs SHM along a straight line and its position is →R, acceleration is →a, velocity is →v is and force on particle is →f. Then which of the following statement are true?
(i) →v.→a is always + ve
(ii) →v.→R may be -ve
(iii) →f.→R is always -ve
(iv) →v is parallel to →f sometimes
View SolutionStatement 1: If ∣∣→a+→b∣∣=∣∣→a−→b∣∣, then →a and →b are perpendicular to each other. Statement 2: If the diagonal of a parallelogram are equal magnitude, then the parallelogram is a rectangle. Which of the following Statements is/are correct ?
View SolutionThree coplanar vectrors →A,→B and →C have magnitudes 4,3 and 2 respectively. If the angle any two vector is 120∘ then which of the following vector may be equal to 3→A4+→B3+→C2

View Solution→A is a vector with magnitude A, then the unit vector ˆA in the direction →A is
View SolutionIf →r is a vector of magnitude 21 and has direction ratios 2,−3and6, then find →r.
View SolutionThe resultant and dot product of two vectors →aand→b is equal to the magnitude of →a. Show that when the vector →a is doubled , the new resultant is perpendicular to →b .
View SolutionIf →a,→b,→c are non coplanar non-zero vectors such that →b×→c=→a,→a×→b=→c and →c×→a=→b , then which of the following is not true
View Solution