A particle moves along the straight line . Which coordinate changes at faster rate?
x- coordinate
y- coordinate
Both x and y coordinates
Data insufficient
The correct Answer is:2
- coordinate changes at faster rate.
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - GEOMETRY
7 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DEFINITION & TYPES OF VECTOR
6 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - BEGINNER S BOX 12
4 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
A particle moves along the curve 12y=x3. . Which coordinate changes at faster rate at x=10?
View SolutionA particle moves along a straight line on y-axis. The distance of the particle from O varies with time and is given by : y=20t−t2. The distance travelled by the particle before it momentarily comes to rest is
View SolutionA particle moves along the curve x2=2y. At what point, ordinate increases at the same rate as abscissa increases ?
View SolutionA particle moves along a straight line OX. At a time t (in seconds) the distance x (in metre) of the particle is given by x=40+12t−t3. How long would the particle travel before coming to rest ?
View SolutionA particle moves along a straight line OX. At a time t(in second), the distance x (in metre) of the particle from O is given by
x=40+12t−t3
How long would the particle travel before coming to rest ?
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionThe figure shows velocity-time graph of a particle moving along a straight line. Identify the correct statement.
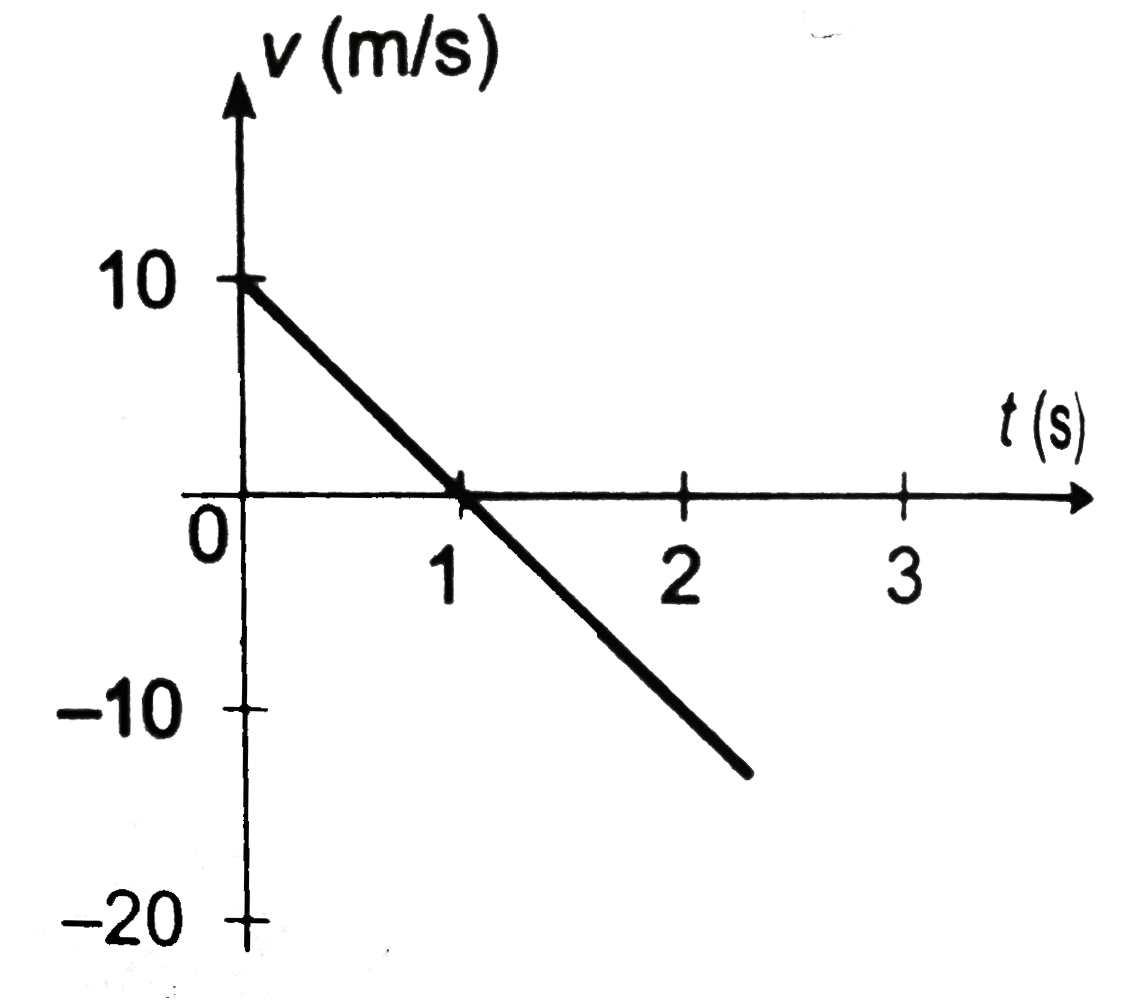
View SolutionIf a particle is moving along straight line with increasing speed, then
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View SolutionA particle moves along a straight line and its position as a function of time is given by x=t6(3)−3t6(2)+3t+3, then particle
View Solution
