Calculate the area enclosed by shown ellipse
2π
3π
6π
32π
The correct Answer is:A
To calculate the area enclosed by the given ellipse, we will follow these steps:
Step 1: Identify the semi-major and semi-minor axes
- The semi-major axis (a) is the longest radius of the ellipse, while the semi-minor axis (b) is the shortest radius.
- From the problem, we know that the semi-major axis is represented by the distance from the center of the ellipse to the edge along the x-axis, and the semi-minor axis is represented by the distance from the center to the edge along the y-axis.
Step 2: Determine the lengths of the semi-major and semi-minor axes
- The length of the semi-major axis a can be calculated as the difference between the maximum and minimum x-coordinates of the ellipse.
- Given that the x-coordinates range from 4 to 6, we calculate:
a=6−42=1 unit
- The length of the semi-minor axis b can be calculated as the difference between the maximum and minimum y-coordinates of the ellipse.
- Given that the y-coordinates range from 3 to 4, we calculate:
b=4−32=0.5 unit
Step 3: Use the formula for the area of an ellipse
- The area A of an ellipse is given by the formula:
A=π×a×b
- Substituting the values of a and b:
A=π×1×0.5=0.5π square units
Final Answer
The area enclosed by the ellipse is 0.5π square units.
---
- The semi-major axis (a) is the longest radius of the ellipse, while the semi-minor axis (b) is the shortest radius.
- From the problem, we know that the semi-major axis is represented by the distance from the center of the ellipse to the edge along the x-axis, and the semi-minor axis is represented by the distance from the center to the edge along the y-axis.
- The length of the semi-major axis a can be calculated as the difference between the maximum and minimum x-coordinates of the ellipse.
- Given that the x-coordinates range from 4 to 6, we calculate:
a=6−42=1 unit
- The length of the semi-minor axis b can be calculated as the difference between the maximum and minimum y-coordinates of the ellipse.
- Given that the y-coordinates range from 3 to 4, we calculate:
b=4−32=0.5 unit
- The area A of an ellipse is given by the formula:
A=π×a×b
- Substituting the values of a and b:
A=π×1×0.5=0.5π square units
The area enclosed by the ellipse is 0.5π square units.
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:BEGINNER S BOX 1
Explore 2 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:BEGINNER S BOX 2
Explore 3 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V B
Explore 19 Videos
Similar Questions
Calculate the area enclosed by the curve 4≤x2+y2≤2(|x|+|y|).
View Solution(a). Calculate the area enclosed by a circle of radius 0.56m to the correct number of significant figures.
(b) . Calculate the area enclosed by a circle of diameter 1.12m to the correct number of significant figures.
View SolutionCalculate the area enclosed by the parabola y2=x+3y and the Y-axis.
View SolutionCalculate the area enclosed under the curve f(x)=x2 between the limits x=2 and x=3 (figure)
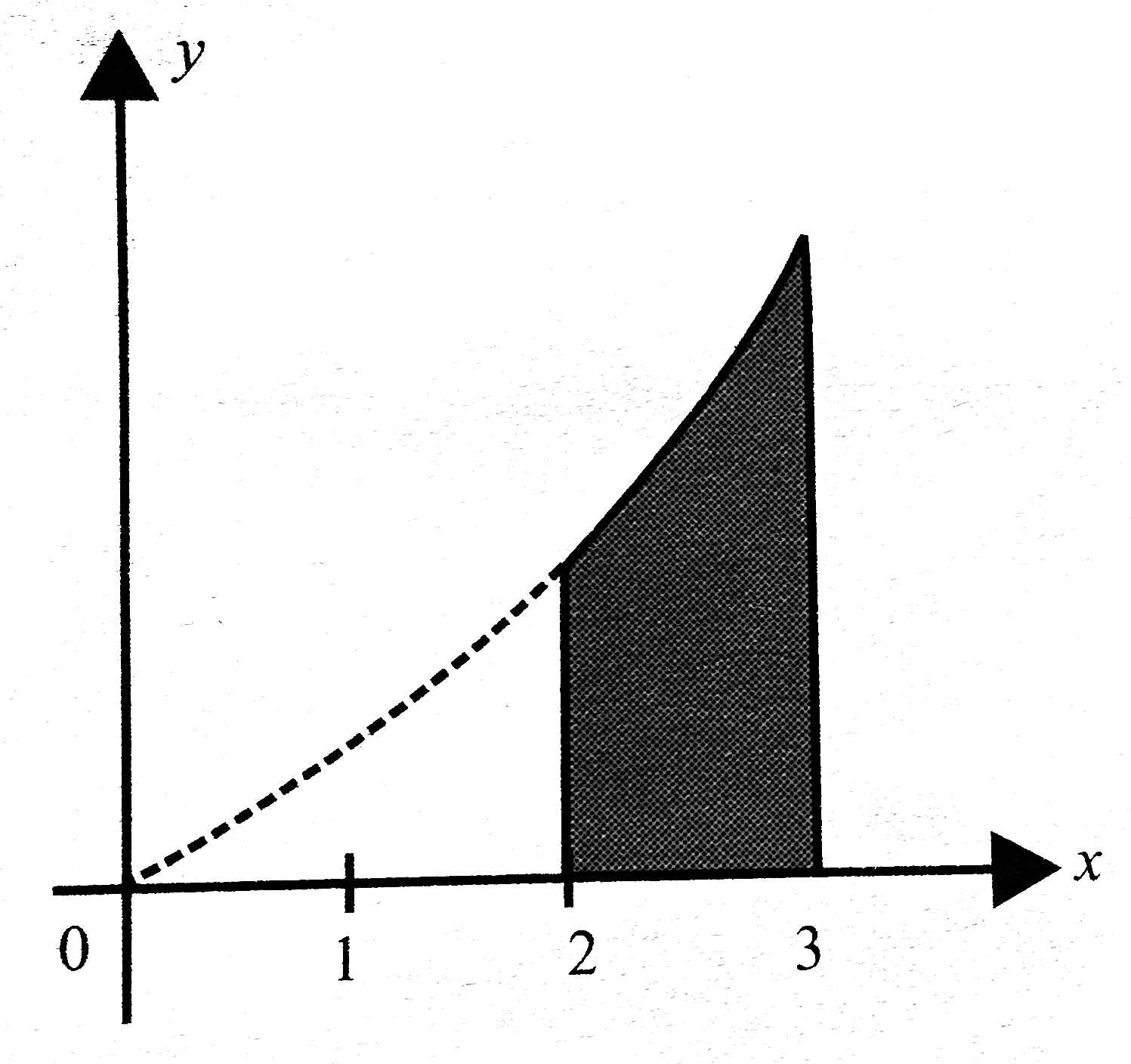
View SolutionFind the area enclosed by the ellipse x2a2+y2b2=1.
View SolutionFind the area enclosed by the ellipse x225+y216=1 .
View SolutionCalculate area enclosed by a circle of diameter 1.06 m to correct number of significant figures.
View SolutionFind the point (α,β) on the ellipse 4x2+3y2=12, in the first quadrant, so that the area enclosed by the lines y=x,y=β,x=α , and the x-axis is maximum.
View SolutionA copper wire, when bent in the form of a square, encloses an area of 484 cm2. If the same wire is bent in the form of a circle, find the area enclosed by it. (Use π=227).
View SolutionDraw the rough sketch of y2+1=x, x≤2. Find the area enclosed by the curve and the line x=2.
View Solution