Find the solution set of the inequality $sin x > \frac{1}{2} .$

Video Solution

Text Solution

Verified by Experts

When $sin x = \frac{1}{2}$ , the two values of x between 0 and $2 π$ and $π / 6$ and $5 π / 6$
From the graph of $y = sin x$ , it is obvious that between 0 and $2 π$ ,
$sin x > \frac{1}{2}$ for $\frac{π}{6} < x < 5 π / 6$
Here, $sin x > 1 / 2$
$\Rightarrow 2 n π + π / 6 < x < 2 n π + 5 π / 6, n \in I$

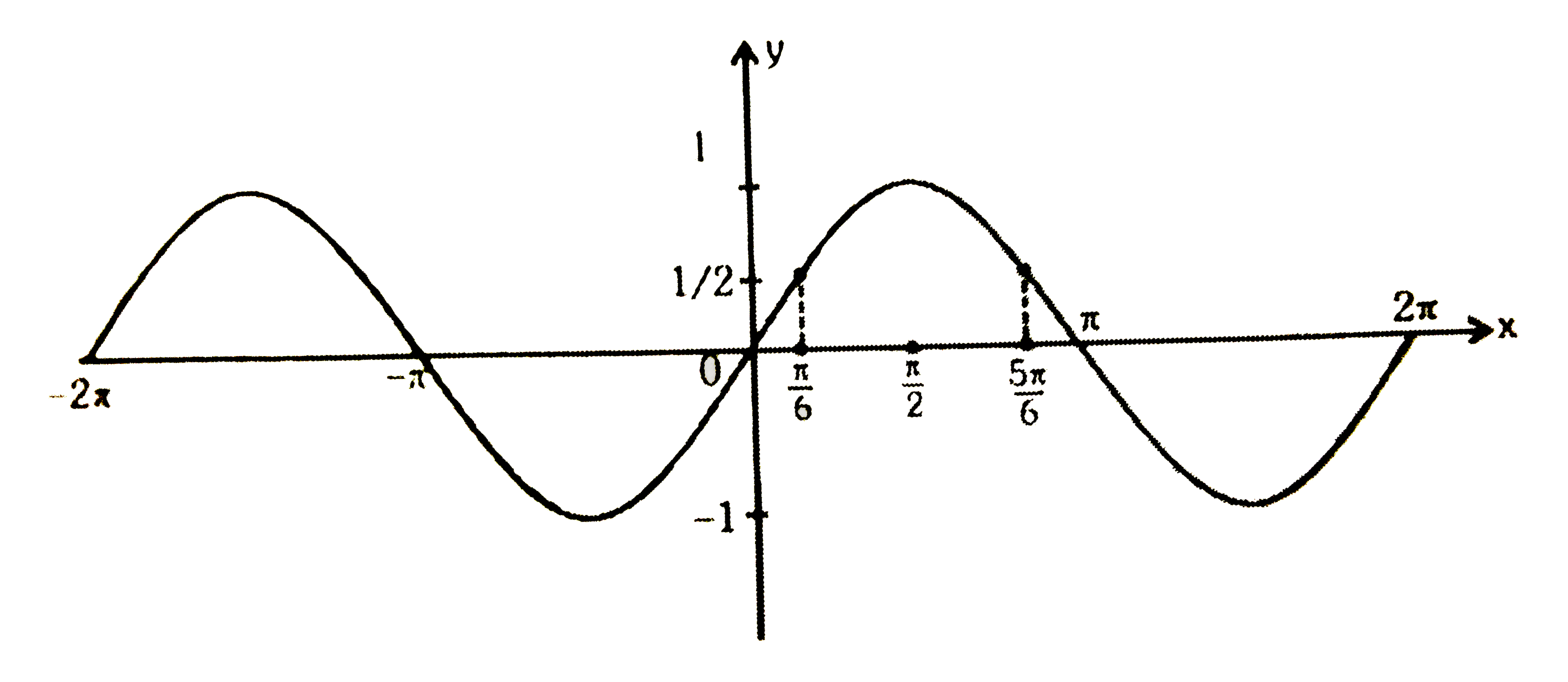
Thus, the required solution set is $\cup n \in I (2 n π + \frac{π}{6}, 2 n π + \frac{5 π}{6})$ Ans.

Updated on:21/07/2023

|

Class 11 MATHS LOGARITHM AND ITS APPLICATIONS

Topper's Solved these Questions

Similar Questions

ALLEN-BASIC MATHS,LOGARITHIM, TRIGNOMETRIC RATIO AND IDENTITIES AND TRIGNOMETRIC EQUATION -EXERCISE (JM)

Home
Ask Doubt
Profile