The EMF generated across a thermocouple with cold junction at 0∘C , is
E=aθ+bθ2
with a =30μV(.∘C)−1 and b=0.08μV(.∘C)−2
At E=6mV. The hot junction temperature is about
14∘C
144∘C
323∘C
640∘C
To solve the problem, we start with the equation for the electromotive force (EMF) generated across a thermocouple:
E=aθ+bθ2
where:
- E is the EMF,
- θ is the temperature of the hot junction,
- a=30μV/°C,
- b=0.08μV/°C2.
Given that E=6mV=6000μV, we can substitute the values into the equation:
1. Rearranging the equation:
bθ2+aθ−E=0
This is a quadratic equation in the form Aθ2+Bθ+C=0, where:
- A=b=0.08μV/°C2,
- B=a=30μV/°C,
- C=−6000μV.
2. Applying the quadratic formula:
The solutions for θ can be found using the quadratic formula:
θ=−B±√B2−4AC2A
Substituting the values:
θ=−30×10−6±√(30×10−6)2−4×0.08×10−6×(−6000×10−6)2×0.08×10−6
3. Calculating the discriminant:
B2=(30×10−6)2=900×10−12=9×10−10
4AC=4×0.08×10−6×6000×10−6=1920×10−12=1.92×10−9
Thus, the discriminant becomes:
B2−4AC=9×10−10+1.92×10−9=2.82×10−9
4. Finding the square root of the discriminant:
√2.82×10−9≈5.3×10−5
5. Substituting back into the quadratic formula:
θ=−30×10−6±5.3×10−52×0.08×10−6
Calculating the two potential solutions for θ:
- Using the positive root:
θ=−30×10−6+5.3×10−50.16×10−6=5.3×10−5−30×10−60.16×10−6=2.3×10−50.16×10−6≈143.75°C
- Using the negative root would yield a negative temperature, which is not physically meaningful in this context.
6. Final result:
Therefore, the temperature of the hot junction is approximately:
θ≈144°C
- E is the EMF,
- θ is the temperature of the hot junction,
- a=30μV/°C,
- b=0.08μV/°C2.
bθ2+aθ−E=0
This is a quadratic equation in the form Aθ2+Bθ+C=0, where:
- A=b=0.08μV/°C2,
- B=a=30μV/°C,
- C=−6000μV.
The solutions for θ can be found using the quadratic formula:
θ=−B±√B2−4AC2A
Substituting the values:
θ=−30×10−6±√(30×10−6)2−4×0.08×10−6×(−6000×10−6)2×0.08×10−6
B2=(30×10−6)2=900×10−12=9×10−10
4AC=4×0.08×10−6×6000×10−6=1920×10−12=1.92×10−9
Thus, the discriminant becomes:
B2−4AC=9×10−10+1.92×10−9=2.82×10−9
√2.82×10−9≈5.3×10−5
θ=−30×10−6±5.3×10−52×0.08×10−6
Calculating the two potential solutions for θ:
- Using the positive root:
θ=−30×10−6+5.3×10−50.16×10−6=5.3×10−5−30×10−60.16×10−6=2.3×10−50.16×10−6≈143.75°C
- Using the negative root would yield a negative temperature, which is not physically meaningful in this context.
Therefore, the temperature of the hot junction is approximately:
θ≈144°C
Similar Questions
For a copper-iron and a chromel-alumel thermocouple, the plots between thermoelectric emf and the temperature θ of the hot junction (when the cold junction is at 0∘C)are found to satisfy approximately the parabola equation V=αθ+12βθ2 with
α=14μV∘C−1β=−0.04V∘C−2 (copper-iron)
α=41μCV∘C−1,β=−0.002V∘C−2 (chromel-alumel)
Which of the two thermocouples would you use to measure temperature in the range of a about 500∘C to 600∘C?
View SolutionThe emf ɛ of a Cu-Fe thermocouple varies with the temperature θ of the hot junction (cold junction at 0∘C ), as ɛ(μV)=14θ−0.02θ2 Determine the neutral temperature.
View SolutionThe thermo emf of a thermocouple , one junction of which is kept at 0∘C , is given by ɛ=at+bt2 where a and b constants of the thermocouple . Calculate the neutral temperature and peltier and Thomson coefficients.
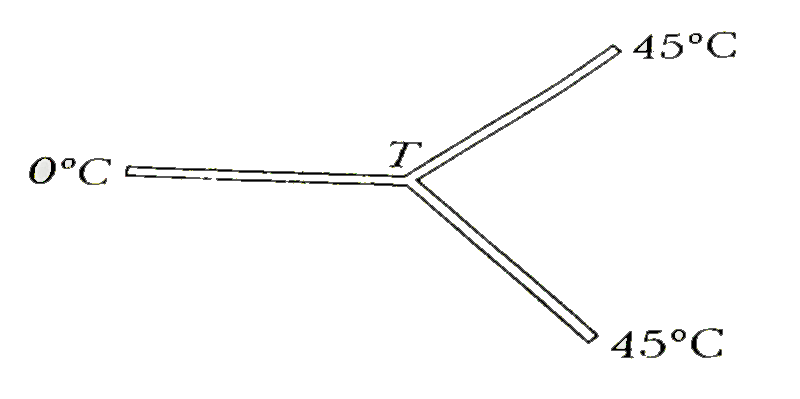
View SolutionThree identical rods have been joined at a junction to make it a Y shape structure. If two free ends are maintained at 45∘C and the end is at 0∘C, then what is the junction temperature T?
View SolutionThermo e.m.f. E of a Cu-Fe thermocouple varies with the temperature θ of the hot junction ( cold juction 0∘C) as E(μV)=12θ−0.02θ2.
Determine:-
(a) Neutral temperature of the termocouple
(b) Temperature of inversion, assuming that cold junction is at 20∘C.
(c) Value of Seebeck coefficient at neutral temperature
View SolutionThe temperature of the cold junction of thermo-couple is 0∘C and the temperature of hot junction is T∘C . The e.m.f . is E=16T−0.04T2μ volts. The temperature of inversion is
View SolutionThe constants aandb for the pair silver-lead are 2.50μV∘C−1and0.012μV∘C−2 respectively. For a silver-lead thermocouple with colder junction at 0∘C,
View SolutionThe constant of a thermocouple is 7.6μV/K, the temperature of its cold junction is −80∘C (dry ice), and that of the hot 327∘C (molten lead). What charge will flow through the thermocouple, if the hot junction absorbs quantity of heat equal to one joule? The efficiency of the thermocouple is 20%.
View SolutionWith the cold junction at 0∘C the neutral temperature for a thermo-couple is obtained at 270∘C.
The cold junction temperature is now lowered to −10∘C Obta in the
(a) neutral temperature
(b) the temperature of inversion in this case.
View SolutionWith the cold junction at 0∘C the neutral temperature for a thermo-couple is obtained at 270∘C.
The cold junction temperature is now lowered to −10∘C Obta in the
(a) neutral temperature
(b) the temperature of inversion in this case.
View Solution
