Question

A body released from a great height and falls freely towards the earth. Another body is released from the same height exactly one second later. Then the separation between the two bodies, two seconds after the release of the second body is

Answer

`u=7.29 ms^(-1), t=1s`

Explanation

Let 't' be the time after which the stone hits the object and `theta` be the abgle which the velocity vector `vec(u)` makes with horizontal. According to question, we have following three conditions.

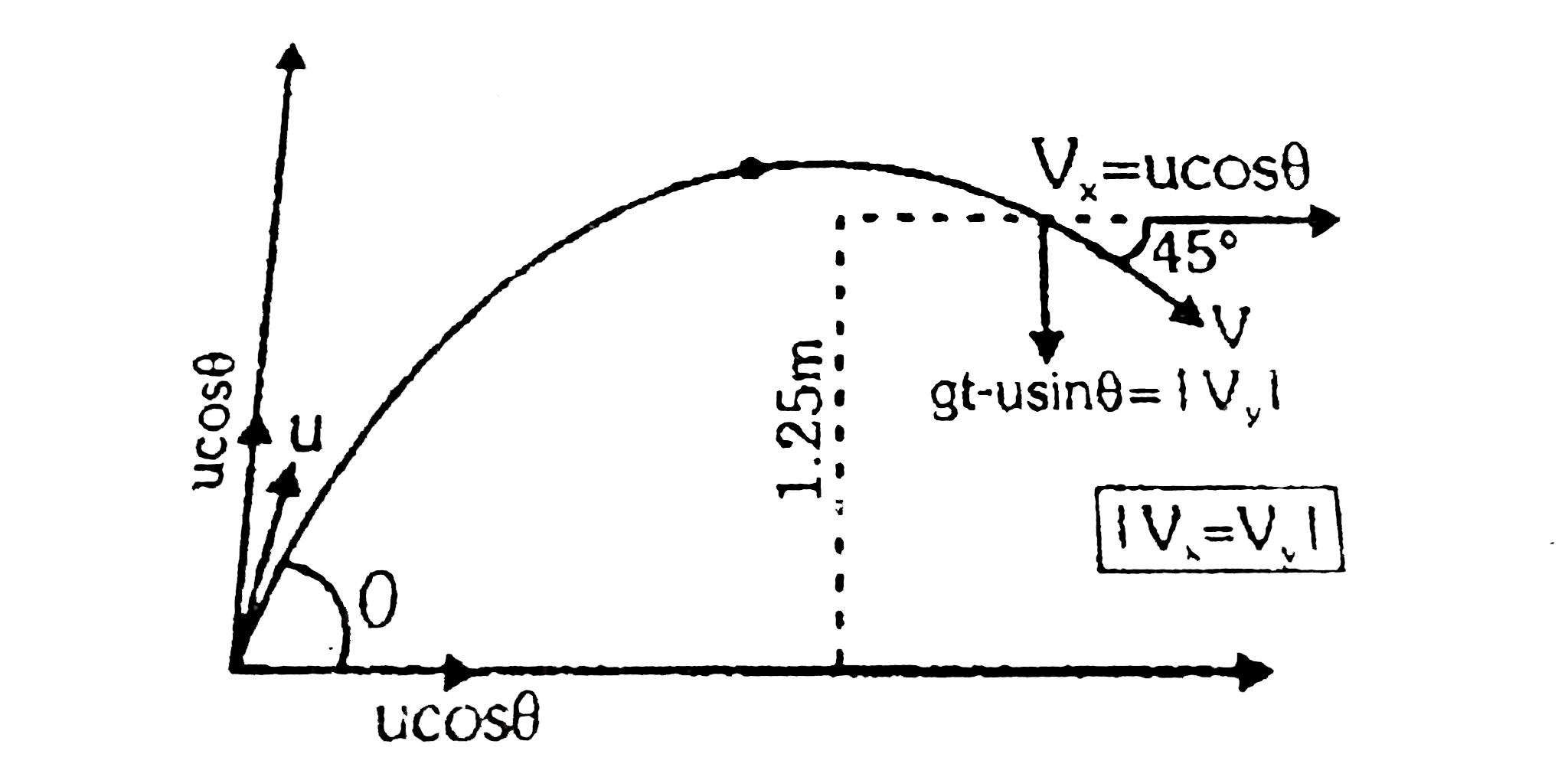
(i) Vertical displacement of stome is `1.25 m`
`:' 1.25=(u sin theta)t-1/2 g t^(2)` where `g=10 m//s^(2)`
`rArr (u sin theta)t=1.25+5t^(2)` ...(i)
(ii) horizontal displacement of stone
`=3 +` dispplacement of object A.
Therefore `(u cos theta)t=3 +1/2 at^(2)`
where `a=1.5 m//s^(2) rArr (u cos theta)t=3 +0.75 t^(2)` ...(ii)
Horizontal component of velocity (of stone)
`=` vertical component (because velocity vector is inclined) at `45^(@)` with horizontal.
Therefore `(u cos theta)=g t-(u sin theta)` ...(iii)
The right hand side is written `g t-u sin theta` because the stone is in its downward motion.
Therefore, `g t gt u sin theta`
In upward motion `u sin theta gt g t`
Multiplying equation (iii) with t we can write,
`(u cos theta) t+(u sin theta)t=10 t^(2)` ...(iv)
Now `(iv)-(ii)-(i)` gives `4.25 t^(2)-4.25=0` or `t=1 s`
Substituting `t=1s` in (i) and (ii) we get
`u sin theta=6.25 m//s`
`rArr u_(y)=6.25 m//s` and `u cos theta=3.75 m//s`
`rArr u_(x)=3.75 m//s` therefore `vec(u)=u_(x)hat(i)+u_(y)hat(j)`
`rArr vec(u)=(3.75hat(i)+6.25hat(j)) m//s`