Which of the following relations representing displacement x (t) of particle describes motion with constant acceleration?
The correct Answer is:C
To determine which of the given relations for displacement x(t) describes motion with constant acceleration, we need to analyze each option by differentiating the displacement function to find the velocity and then the acceleration. Constant acceleration means that the acceleration does not depend on time.
1. Understand the Concept of Constant Acceleration:
- Constant acceleration means that the acceleration a is a constant value and does not change with time t or displacement x.
2. Differentiate the Displacement Function:
- The first step is to differentiate the displacement function x(t) to find the velocity v(t):
v(t)=dxdt
3. Differentiate Again to Find Acceleration:
- Next, differentiate the velocity function to find the acceleration a(t):
a(t)=dvdt
4. Analyze Each Option:
- Option 1: x(t)=6−7t2
- Differentiate once:
v(t)=ddt(6−7t2)=−14t
- Differentiate again:
a(t)=ddt(−14t)=−14
- Since a(t)=−14 is a constant, this option represents motion with constant acceleration.
- Option 2: x(t)=6+7t3
- Differentiate once:
v(t)=ddt(6+7t3)=21t2
- Differentiate again:
a(t)=ddt(21t2)=42t
- Since a(t)=42t depends on t, this option does not represent constant acceleration.
- Option 3: x(t)=6+7t
- Differentiate once:
v(t)=ddt(6+7t)=−7t2
- Differentiate again:
a(t)=ddt(−7t2)=14t3
- Since a(t)=14t3 depends on t, this option does not represent constant acceleration.
- Option 4: x(t)=6+7√t
- Differentiate once:
v(t)=ddt(6+7√t)=72√t
- Differentiate again:
a(t)=ddt(72√t)=−74t3/2
- Since a(t)=−74t3/2 depends on t, this option does not represent constant acceleration.
5. Conclusion:
- The only option that describes motion with constant acceleration is Option 1: x(t)=6−7t2.
- Constant acceleration means that the acceleration a is a constant value and does not change with time t or displacement x.
- The first step is to differentiate the displacement function x(t) to find the velocity v(t):
v(t)=dxdt
- Next, differentiate the velocity function to find the acceleration a(t):
a(t)=dvdt
- Option 1: x(t)=6−7t2
- Differentiate once:
v(t)=ddt(6−7t2)=−14t
- Differentiate again:
a(t)=ddt(−14t)=−14
- Since a(t)=−14 is a constant, this option represents motion with constant acceleration.
- Differentiate once:
v(t)=ddt(6+7t3)=21t2
- Differentiate again:
a(t)=ddt(21t2)=42t
- Since a(t)=42t depends on t, this option does not represent constant acceleration.
- Differentiate once:
v(t)=ddt(6+7t)=−7t2
- Differentiate again:
a(t)=ddt(−7t2)=14t3
- Since a(t)=14t3 depends on t, this option does not represent constant acceleration.
- Differentiate once:
v(t)=ddt(6+7√t)=72√t
- Differentiate again:
a(t)=ddt(72√t)=−74t3/2
- Since a(t)=−74t3/2 depends on t, this option does not represent constant acceleration.
- The only option that describes motion with constant acceleration is Option 1: x(t)=6−7t2.
Topper's Solved these Questions
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:Comprehension#1
Explore 3 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:Comprehension#2
Explore 5 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
Similar Questions
Knowledge Check
On the basis of dimensions, decide which of the following relation for the displacement of a particle undergoing simple harmonic motion is not correct :
Ay=asin(2πtT)By=acosωtCy=aTsin(ta)Dy=a√2(sin(2πtT)+cos(2πtT))Which of the following relationships between the acceleration a and the displacement x of a particle executing simple harmonic motion?
Aa=2x2Ba=−2x2Ca=2xDa=−2xWhich of the following x-t graphs does not represent periodic motion?
A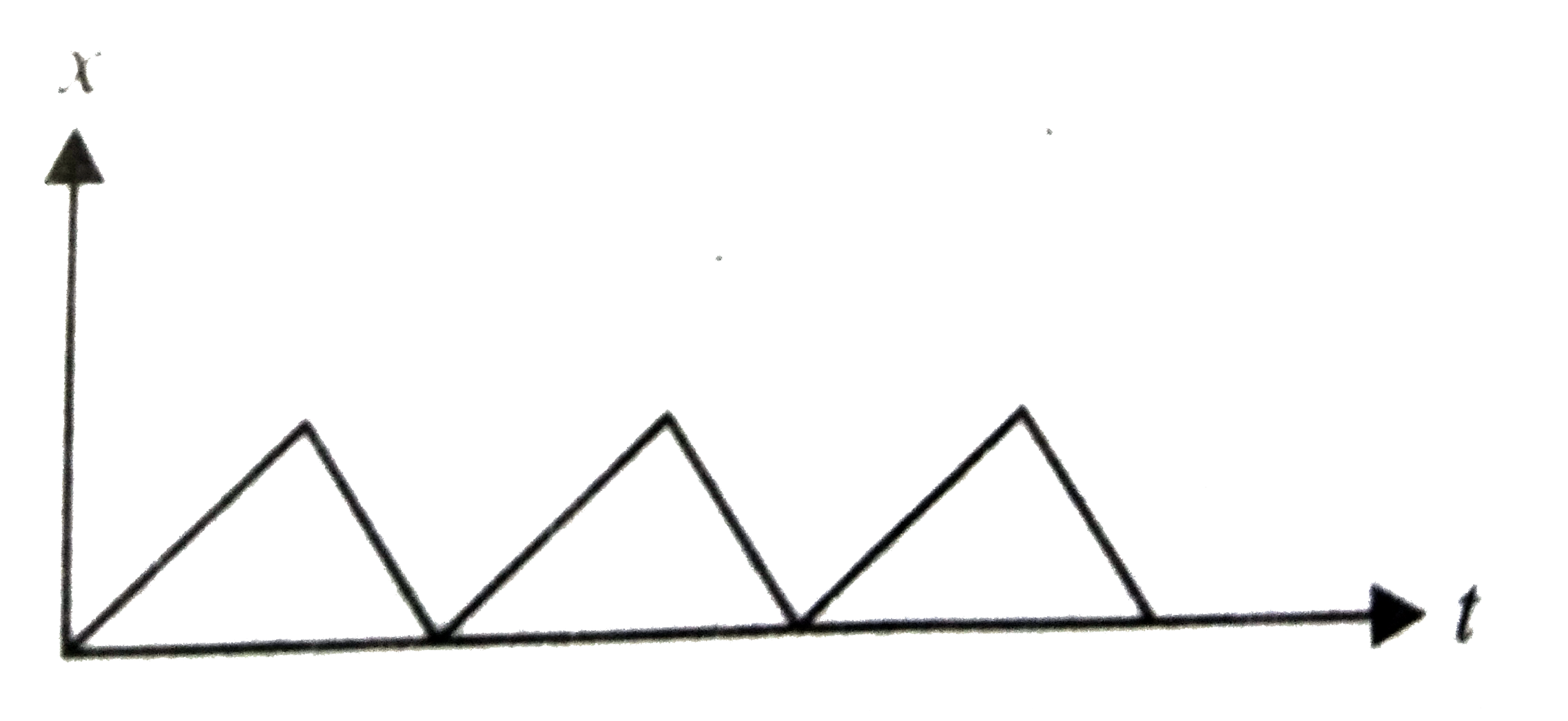 B
B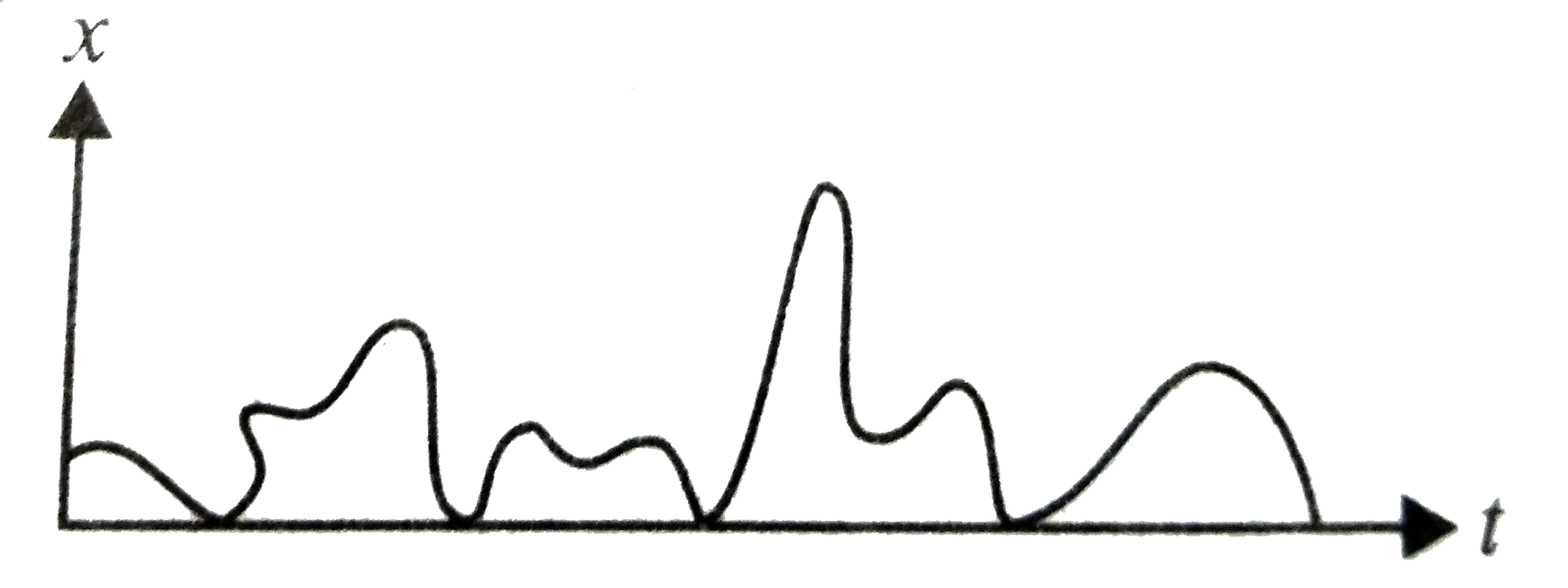 C
C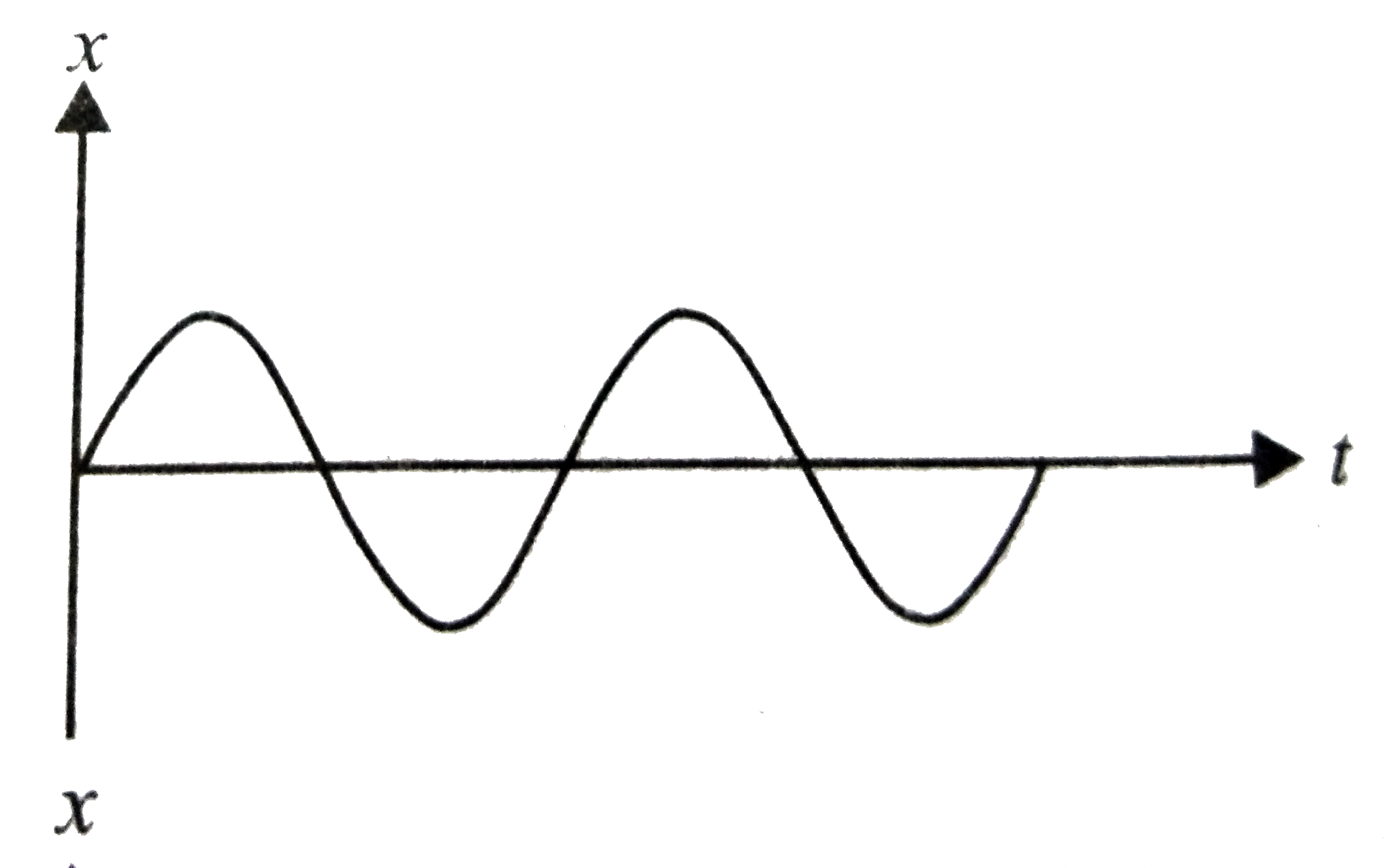 D
D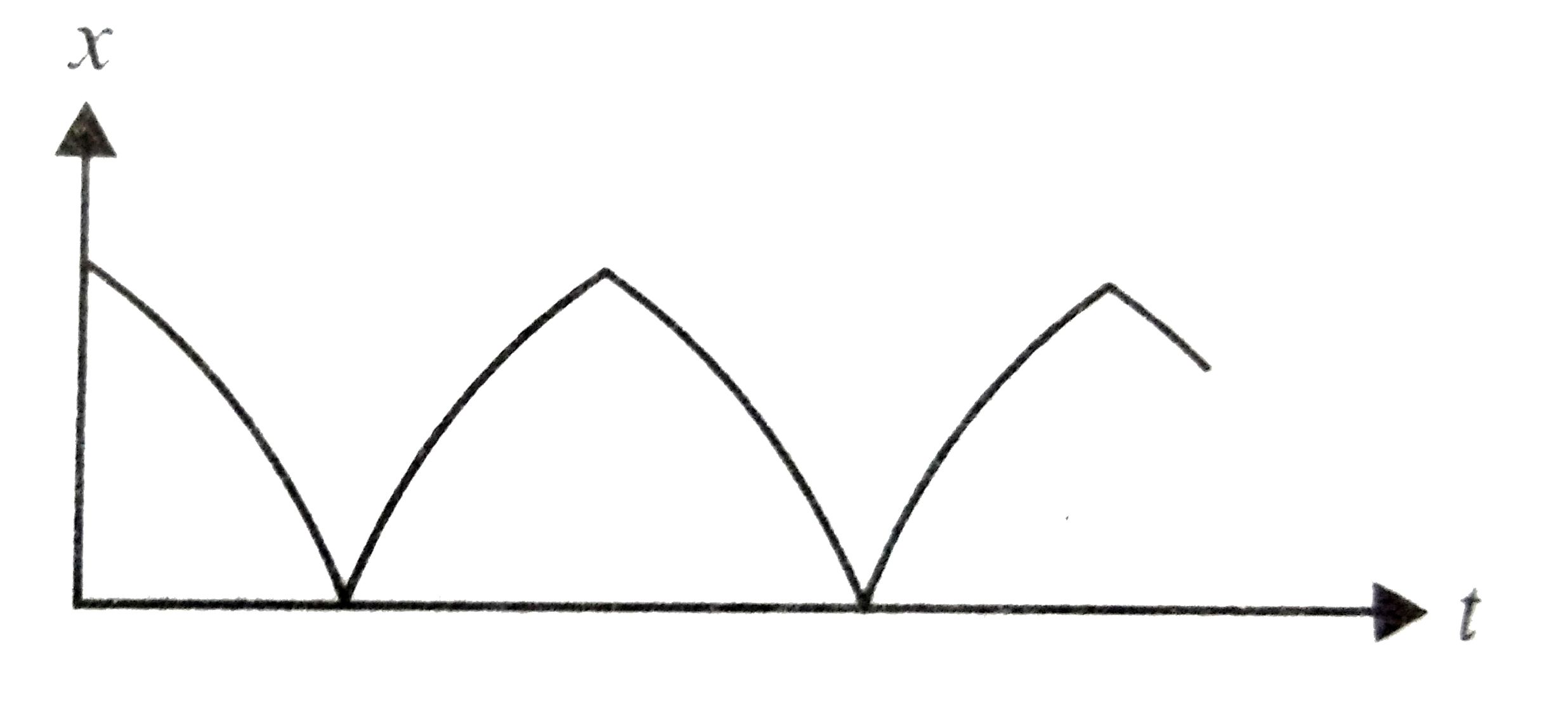
Which of the following relationship between the acceleration, a and the displacement x of a particle involve simple harmonic motion.
(a) a=7.0x (b) a=−200x2 (c) a=−10x (d) a=100x3
View SolutionWhich of the following graphs cannot possibly represent one dimensional motion of a particle?
View SolutionWhich of the following graphs represents the motion of a particle moving with constant velocity?
View SolutionWhich of the following relates to photons both as wave motion and as a stream of particles?
View SolutionWhich of the following graphs cannot possibly represent one dimensional motion of a particle?

View Solution