Assertion : The unit vectors ˆi,ˆjandˆk have of distance and dimensions [MoL1To].
Reason : The product of a scalar and a vector of a new scalar.
The correct Answer is:(A) p, q (B) p, q (C) p, q s (D) r, s
(A) Initially, the potential difference exist between both shells, so positive charge is flow from high to low potential.
Wvery system wants to acquire minimum potential energy if possible for stability. So charge flown to achieve it.
(B) As explained in [A], charge flow does not depends on the size of sphere.
(C) Charge flow through wire until the potential becomes same for both shells.
(D) Potential is same everywhere inside a conducting shell. So no charge is flow through connecting wire, so no heat is produced.
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Comprehension 6
2 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Comprehension 7
3 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exersice-04
1 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Find the unit vector of 4ˆi−3ˆj+ˆk.
View SolutionA unit vector perpendicular to both ˆi+ˆjandˆj+ˆk is
View SolutionAssertion : A vector can have zero magnitude if one of its rectangular components is not zero.
Reason : Scalar product of two vectors cannot be a negative quantity.
View SolutionAssertion: The dot product of one vector with another vector may be scalar or a vector.
Reason: If the product of two vectors is a vector quantity, then product is called a dot product.
View SolutionThe unit vectors ˆi,ˆj and ˆk are as shown below. What will be the magnetic field at O in the following figure
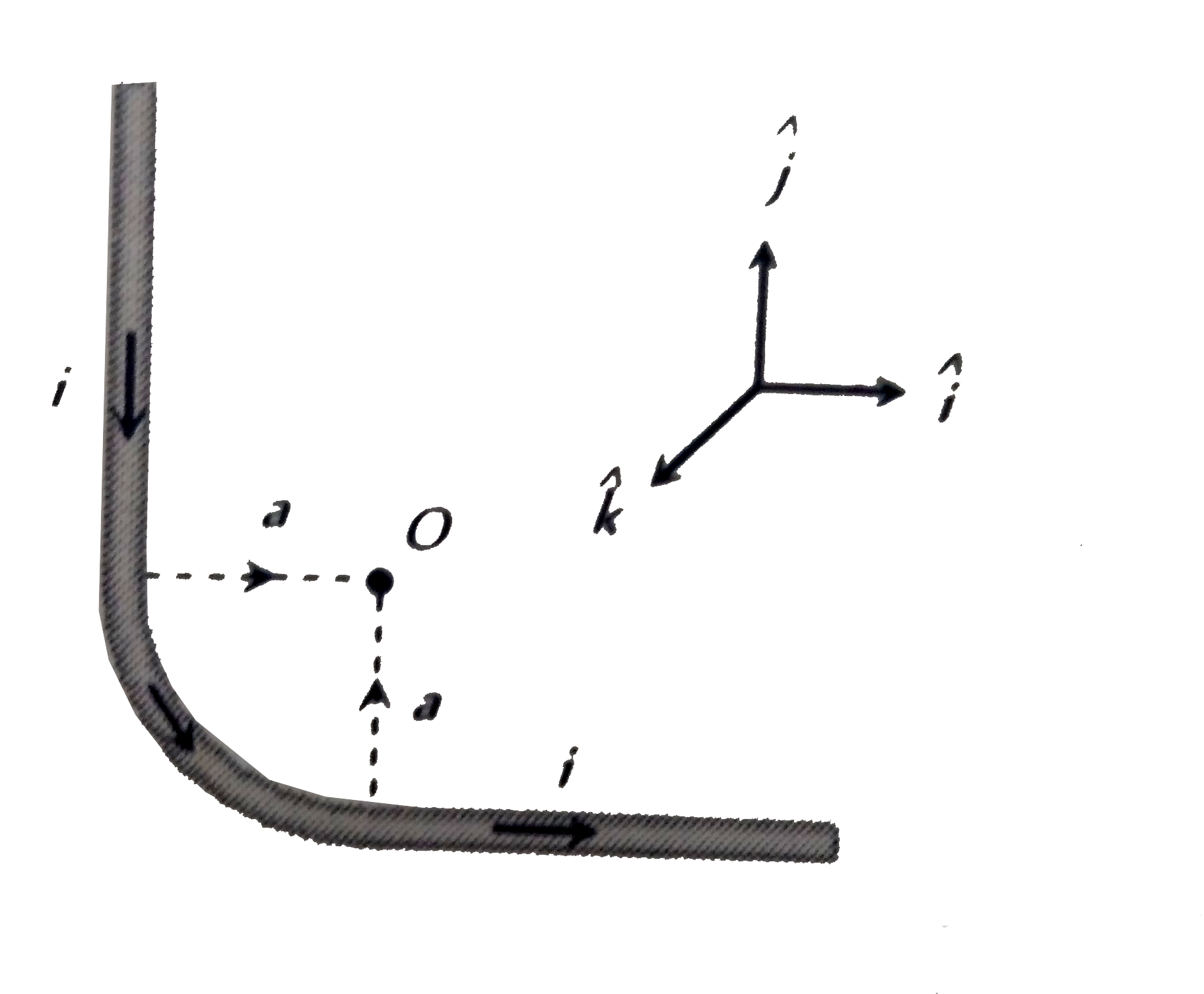
View SolutionThe scalar product of two vectors A=2ˆi+2ˆj−ˆkandB=−ˆj+ˆk ,is given by
View SolutionFind the resultant of vectors →a=ˆi−ˆj+2ˆkand→b=ˆi+2ˆj−4ˆk. Find the unit vector in the direction of the resultant vector.
View SolutionAssertion: Adding a scalar to a vector of the same dimensions is a meanigful algeraic operation.
Reason: The displacement can be added with distance.
View SolutionConsider the two vectors : →L=1ˆi+2ˆj+3ˆk and →l=4ˆi+ˆj+6ˆk. Find the value of the scalar α such that the vector →L−α→l is perpendicular to →L.
View SolutionAssertion: An object can have constant speed but variable velocity.
Reason: Speed is a scalar but velocity is a vector quantity.
View Solution
