A vector →F1 is along the positive X-axis. its vectors product with another vector →F2 is ? where →F2 is along Y-axis
The correct Answer is:2√19,tan−1(3√37)
To solve the problem of finding the vector product (cross product) of two vectors, →F1 and →F2, where →F1 is along the positive X-axis and →F2 is along the Y-axis, we can follow these steps:
Step 1: Define the Vectors
We start by defining the two vectors in a three-dimensional coordinate system:
- Let →F1=F1⋅i, where F1 is the magnitude of →F1 and i is the unit vector in the X-direction.
- Let →F2=F2⋅j, where F2 is the magnitude of →F2 and j is the unit vector in the Y-direction.
Step 2: Write the Cross Product Formula
The cross product of two vectors →A and →B can be calculated using the determinant of a matrix:
\(
vecA \times vecB = \begin{vmatrix}
i & j & k \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{vmatrix}
\)
For our vectors:
- →F1=F1⋅i implies Ax=F1, Ay=0, Az=0.
- →F2=F2⋅j implies Bx=0, By=F2, Bz=0.
Step 3: Set Up the Determinant
Now we can set up the determinant for the cross product:
\(
vecF_(1) \times vecF_(2) = \begin{vmatrix}
i & j & k \\
F1 & 0 & 0 \\
0 & F2 & 0
\end{vmatrix}
\)
Step 4: Calculate the Determinant
Calculating the determinant, we have:
\(
vecF_(1) \times vecF_(2) = i(0 \cdot 0 - 0 \cdot F2) - j(F1 \cdot 0 - 0 \cdot 0) + k(F1 \cdot F2 - 0 \cdot 0)
\)
This simplifies to:
\(
vecF_(1) \times vecF_(2) = k(F1 \cdot F2)
\)
Step 5: Determine the Direction
The result shows that the vector product →F1×→F2 is along the positive Z-axis, represented by the unit vector k.
Final Result
Thus, the vector product of →F1 and →F2 is:
\(
vecF_(1) \times vecF_(2) = F1 \cdot F2 \cdot k
\)
where k indicates the direction along the positive Z-axis.
We start by defining the two vectors in a three-dimensional coordinate system:
- Let →F1=F1⋅i, where F1 is the magnitude of →F1 and i is the unit vector in the X-direction.
- Let →F2=F2⋅j, where F2 is the magnitude of →F2 and j is the unit vector in the Y-direction.
The cross product of two vectors →A and →B can be calculated using the determinant of a matrix:
\(
vecA \times vecB = \begin{vmatrix}
i & j & k \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{vmatrix}
\)
For our vectors:
- →F1=F1⋅i implies Ax=F1, Ay=0, Az=0.
- →F2=F2⋅j implies Bx=0, By=F2, Bz=0.
Now we can set up the determinant for the cross product:
\(
vecF_(1) \times vecF_(2) = \begin{vmatrix}
i & j & k \\
F1 & 0 & 0 \\
0 & F2 & 0
\end{vmatrix}
\)
Calculating the determinant, we have:
\(
vecF_(1) \times vecF_(2) = i(0 \cdot 0 - 0 \cdot F2) - j(F1 \cdot 0 - 0 \cdot 0) + k(F1 \cdot F2 - 0 \cdot 0)
\)
This simplifies to:
\(
vecF_(1) \times vecF_(2) = k(F1 \cdot F2)
\)
The result shows that the vector product →F1×→F2 is along the positive Z-axis, represented by the unit vector k.
Thus, the vector product of →F1 and →F2 is:
\(
vecF_(1) \times vecF_(2) = F1 \cdot F2 \cdot k
\)
where k indicates the direction along the positive Z-axis.
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exersice-4[B]
14 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-5(A)
15 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - DATA SUFFICIENCY QUESTIONS
3 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
A vector →F1 is along the positive X-axis. If its vectors product with another vector →F2 is zero then →F2 could be
View SolutionA vector →A is along the positive z-axis and its vector product with another vector →B is zero, then vector →B could be :
View SolutionA vector ¯¯¯P is along positive x axis, if ¯¯¯Q is another vector such that (¯¯¯P⋅¯¯¯Q) is zero, then Q should be
View SolutionA vector ¯¯¯Qwhich has a magnitude of 8 is added to the vector ¯¯¯P which lies along the X-axis. The resultant of these two vectors is a third vector ¯¯¯R which lies along the Y-axis and has a magnitude twice that of ¯¯¯P. The magnitude of ¯¯¯P is
View SolutionA vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
View SolutionConsider a vector →F=4ˆi−3ˆj. Another vector that is perpendicular to →F is
View SolutionWrite the vector →F in terms of its component :-
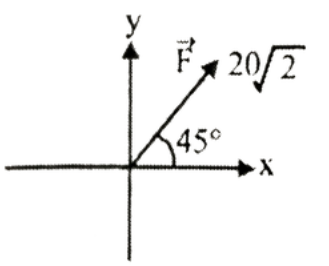
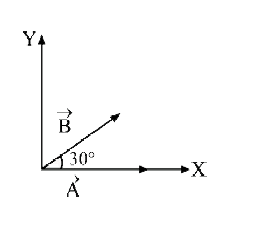
View SolutionVector →A of magnitude 4 units is directed along the positive x-axis. Another vector →B of magnitude 3 units lies in the x-y plane and is directed along 30∘ with the positive x-axis is as shown in figure. The magnitude of dot product →A.→B is:
View SolutionTwo forces →F1=(3N)ˆi−(4N)ˆj and →F2=−(1N)ˆi−(2N)ˆj act on a point object. In the given figure which of the six vectors represents →F1 and →F2 and what is the magnitude of the net forces

View SolutionThe resultant of the forces →F1=4ˆi−3ˆj and →F2=6ˆi+8ˆj is
View Solution
