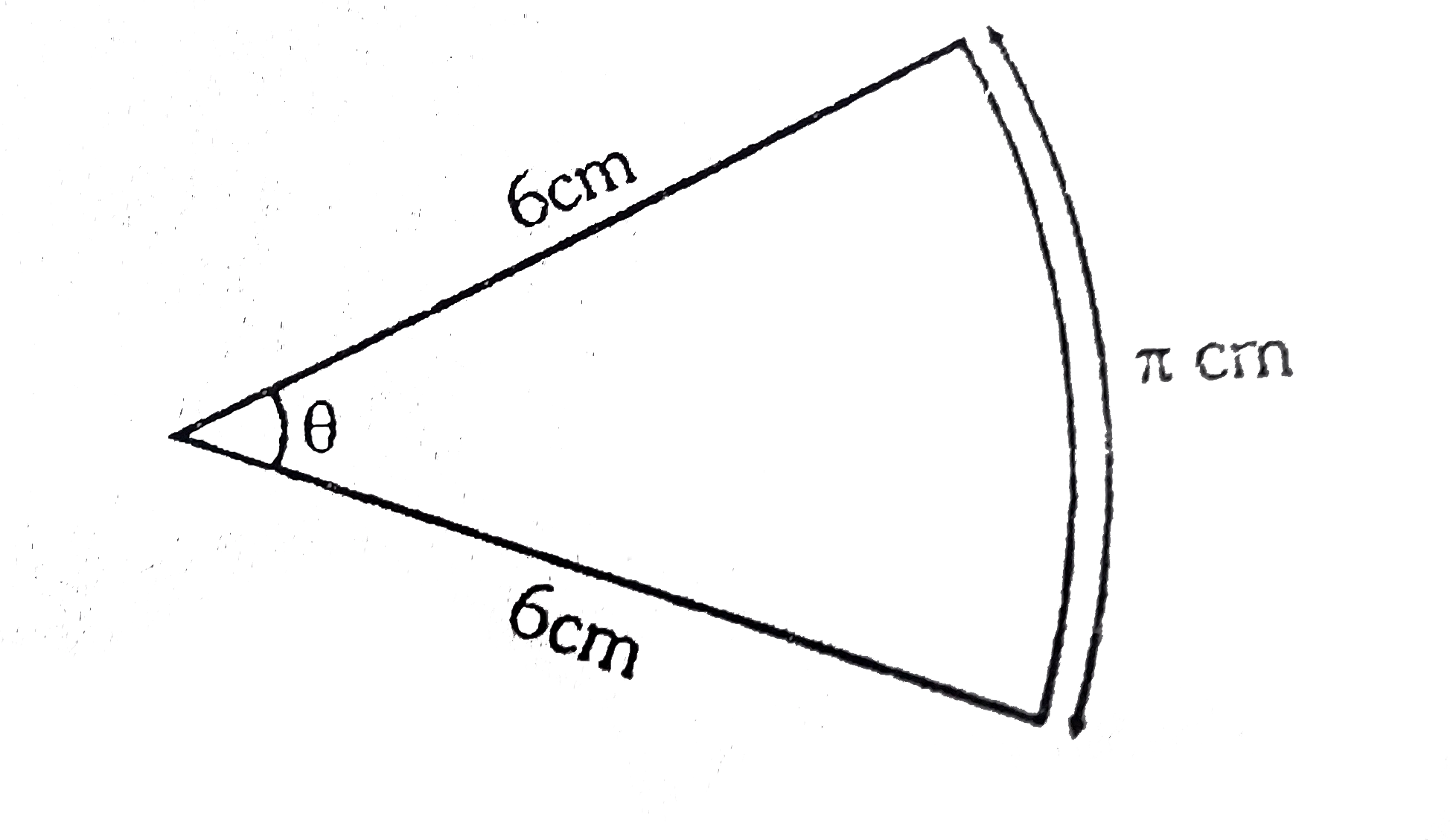
A circular arc of length $π$ cm. Find angle subtended by it at the centre in radian and degree.

Video Solution

Text Solution

Verified by Experts

Comparing this equation with standard quadration $a x^{2} + b x + c = 0$ ,
we have $a = 2, b = - 1, c = - 3$
Now from, $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}, x = \frac{- (- 1) \pm \sqrt{{(- 1)}^{2} - 4 (2) (- 3)}}{2 (2)}$
$x = \frac{1 \pm \sqrt{1 + 24}}{4} = \frac{1 \pm 5}{4} \Rightarrow x_{1} = \frac{+ 6}{4} = \frac{3}{2}$ and $x_{2} = - 1$

Updated on:21/07/2023

|

Class 12 PHYSICS BASIC MATHS

Topper's Solved these Questions

Similar Questions

ALLEN-BASIC MATHS-Question

Home
Ask Doubt
Profile