Three forces are acting on a body to make it in equilibrium , which set can not do it ?
3N,3N,7N
2N,3N,6N
2N, 1N, 1N
8N,6N,1N
The correct Answer is:A, B, D
To determine which set of forces cannot keep a body in equilibrium, we can apply the triangle inequality theorem. The triangle inequality states that for any three sides of a triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the third side.
1. Understanding Equilibrium:
For a body to be in equilibrium under the action of three forces F1, F2, and F3, the vector sum of these forces must equal zero:
F1+F2+F3=0
2. Applying Triangle Inequality:
According to the triangle inequality, for the forces to be in equilibrium, the following conditions must hold:
|F1|+|F2|≥|F3|
|F1|+|F3|≥|F2|
|F2|+|F3|≥|F1|
3. Evaluating Each Option:
We will evaluate each option provided to see if they satisfy the triangle inequality.
- Option A: F1=3, F2=3, F3=7
- Check: 3+3<7 (Does not satisfy)
- Option B: F1=2, F2=3, F3=6
- Check: 2+3<6 (Does not satisfy)
- Option C: F1=2, F2=1, F3=1
- Check: 2+1>1, 1+1=2 (Satisfies)
- Option D: F1=6, F2=1, F3=8
- Check: 6+1<8 (Does not satisfy)
4. Conclusion:
The sets that cannot keep the body in equilibrium are:
- Option A: (3,3,7)
- Option B: (2,3,6)
- Option D: (6,1,8)
Thus, the correct answer is that options A, B, and D cannot keep the body in equilibrium.
For a body to be in equilibrium under the action of three forces F1, F2, and F3, the vector sum of these forces must equal zero:
F1+F2+F3=0
According to the triangle inequality, for the forces to be in equilibrium, the following conditions must hold:
|F1|+|F2|≥|F3|
|F1|+|F3|≥|F2|
|F2|+|F3|≥|F1|
We will evaluate each option provided to see if they satisfy the triangle inequality.
- Check: 3+3<7 (Does not satisfy)
- Option B: F1=2, F2=3, F3=6
- Check: 2+3<6 (Does not satisfy)
- Option C: F1=2, F2=1, F3=1
- Check: 2+1>1, 1+1=2 (Satisfies)
- Option D: F1=6, F2=1, F3=8
- Check: 6+1<8 (Does not satisfy)
The sets that cannot keep the body in equilibrium are:
- Option A: (3,3,7)
- Option B: (2,3,6)
- Option D: (6,1,8)
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-1)
20 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)
7 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
Four forces acting on a particle keep it in equilibrium, then :-
View SolutionThree forces A=(ˆi+ˆj+ˆk),B=(2ˆi−ˆj+3ˆk) and C acting on a body to keep it in equilibrium. The C is :
View SolutionIf the sum of all the forces acting on a body is zero, is it necessarily in equilibrium ? If the sum of all the forces on a particle is zero, is it necessarily in equilibrium?
View SolutionThree forces acting on a body are shown in figure. To have the resultant force only along the y-directon, the magnitude of the minimum additional force needed si
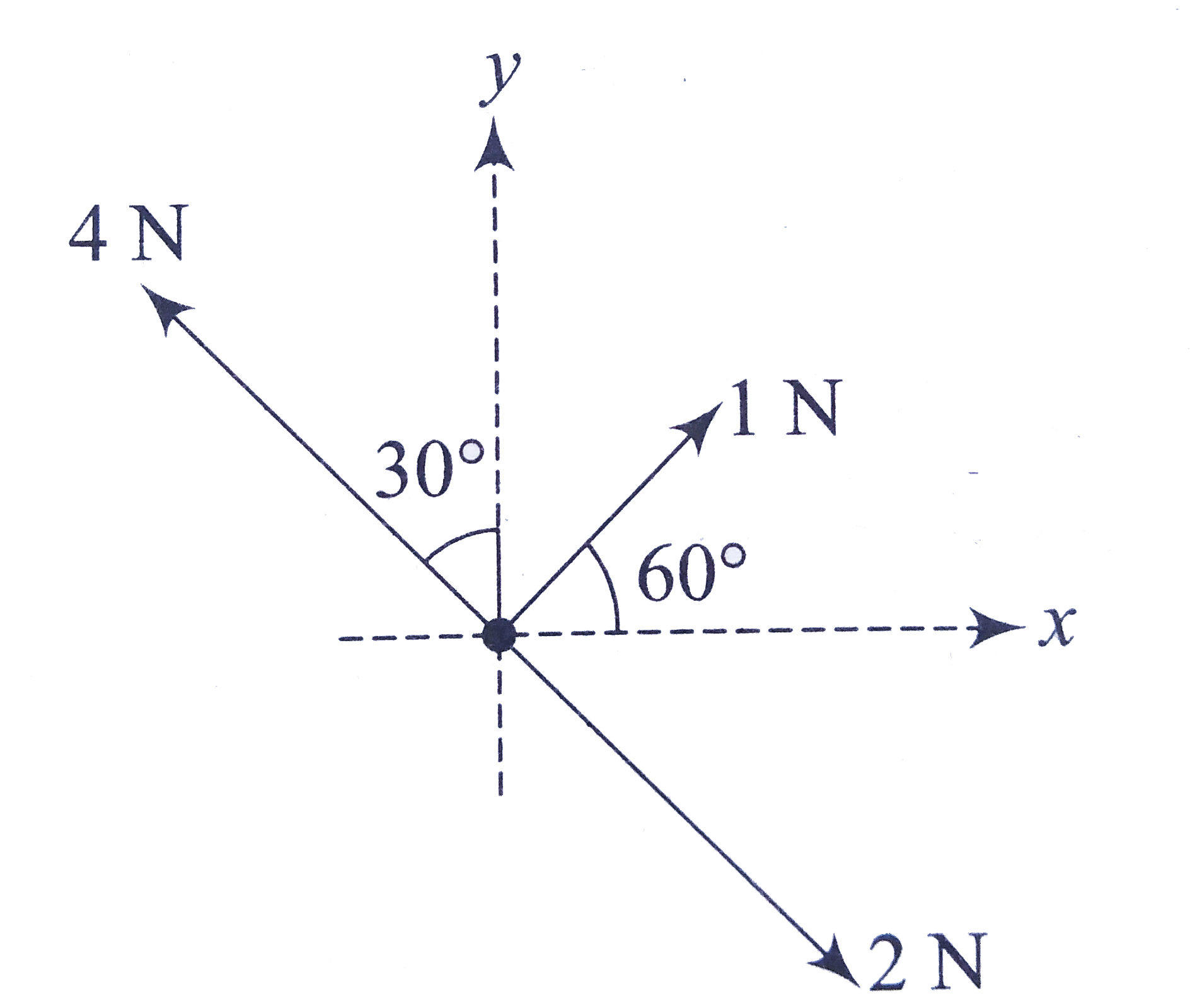
View SolutionThree forces acting on a body are shown in figure. To have the resultant force only along the y-directon, the magnitude of the minimum additional force needed si

View Solution(A) : A body subjected to three concurrent forces cannot be in equilibrium.
(R) : If large number of concurrent forces acting on the same point, then the point may be in equilibrium, even if the vectorial sum of all the force is not zero.
View SolutionFour forces act on a point object. The object will be in equilibrium, if
View SolutionFour forces are acting on a body as shown in figure. The magnitude of resultant of the forces is
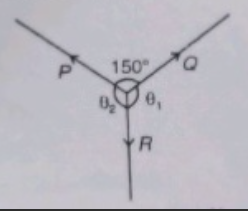
View SolutionP,Q and R are three coplanar forces acting at a point and are in equilibrium. Given P=1N , sinθ1=12 , the value of R is
View SolutionFor a body to be in equilibrium under the combined action of several forces
View Solution
