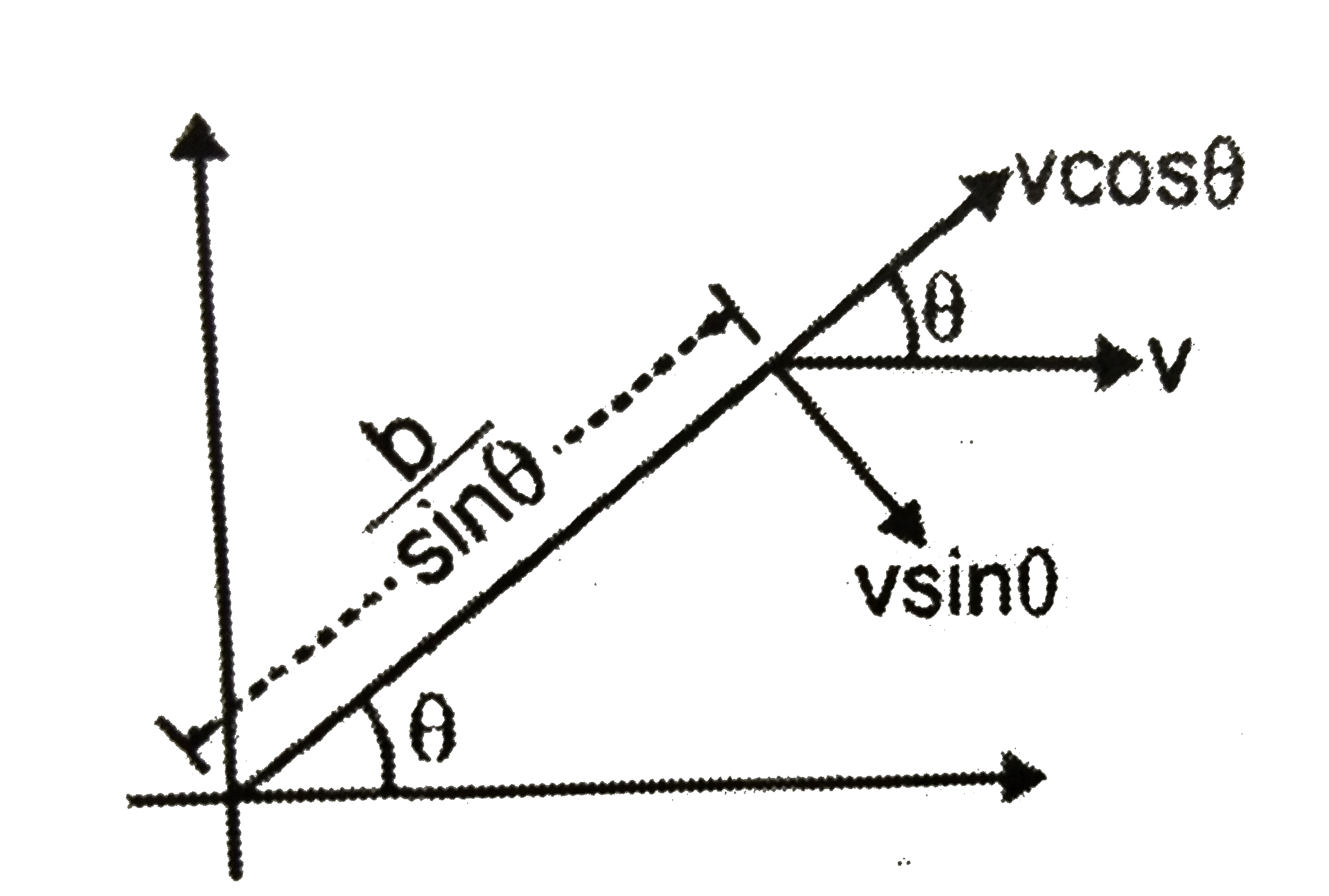
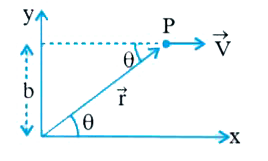
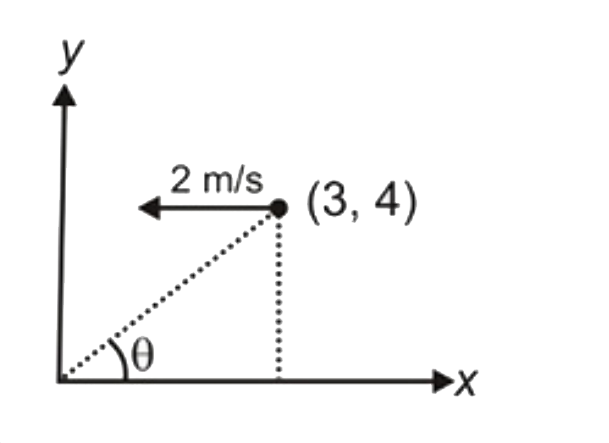
A particle moving parallel to x-axis as shown in figure. such that, at all instant the y-axis component of its position vector is constant and is equal to ‘b’. Find the angular velocity of the particle about the origin.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (S-1)
Explore 8 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:Dynamics of circular motion
Explore 6 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Question
Explore 1 Video
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
Similar Questions
A particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
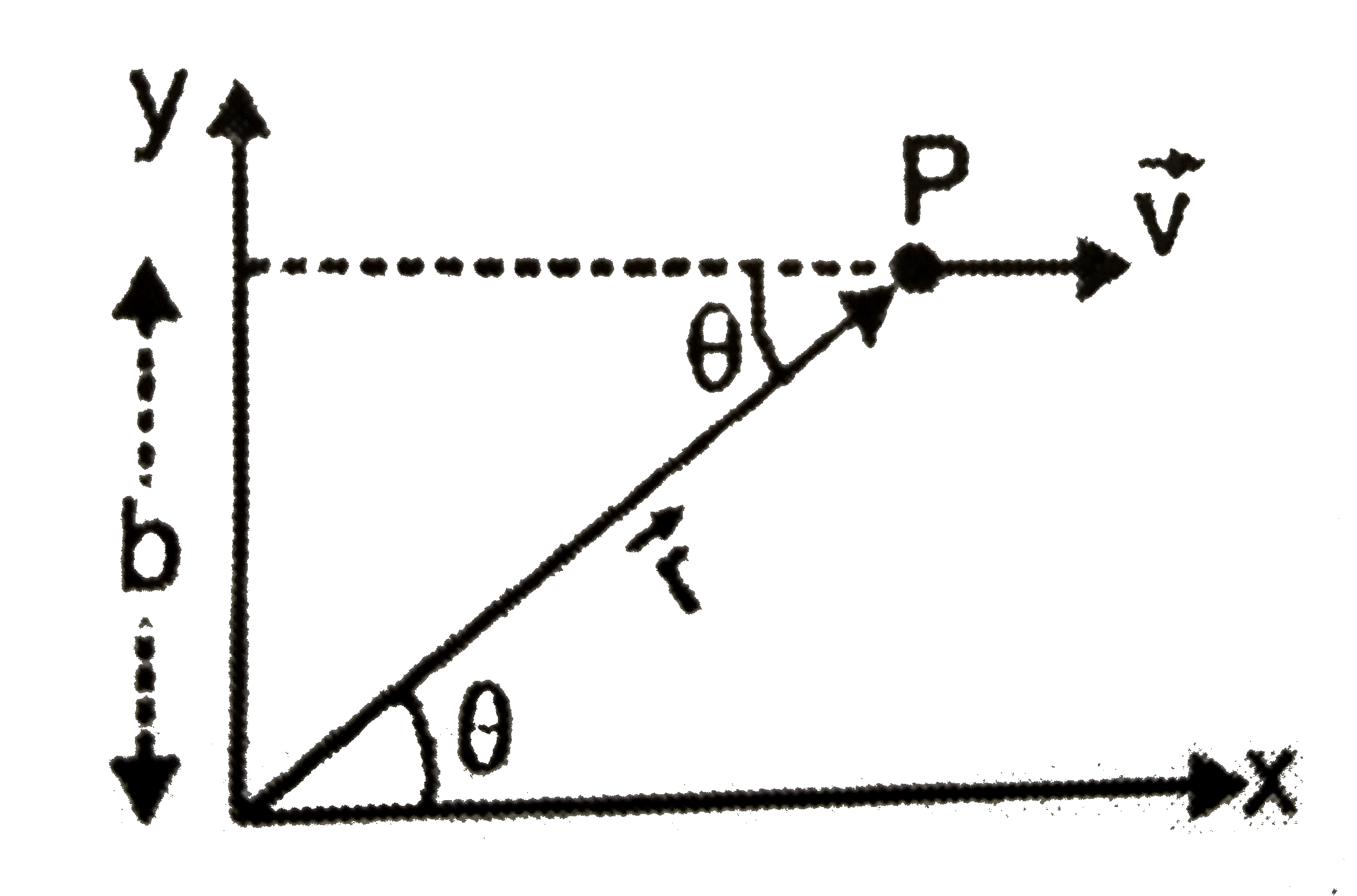
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
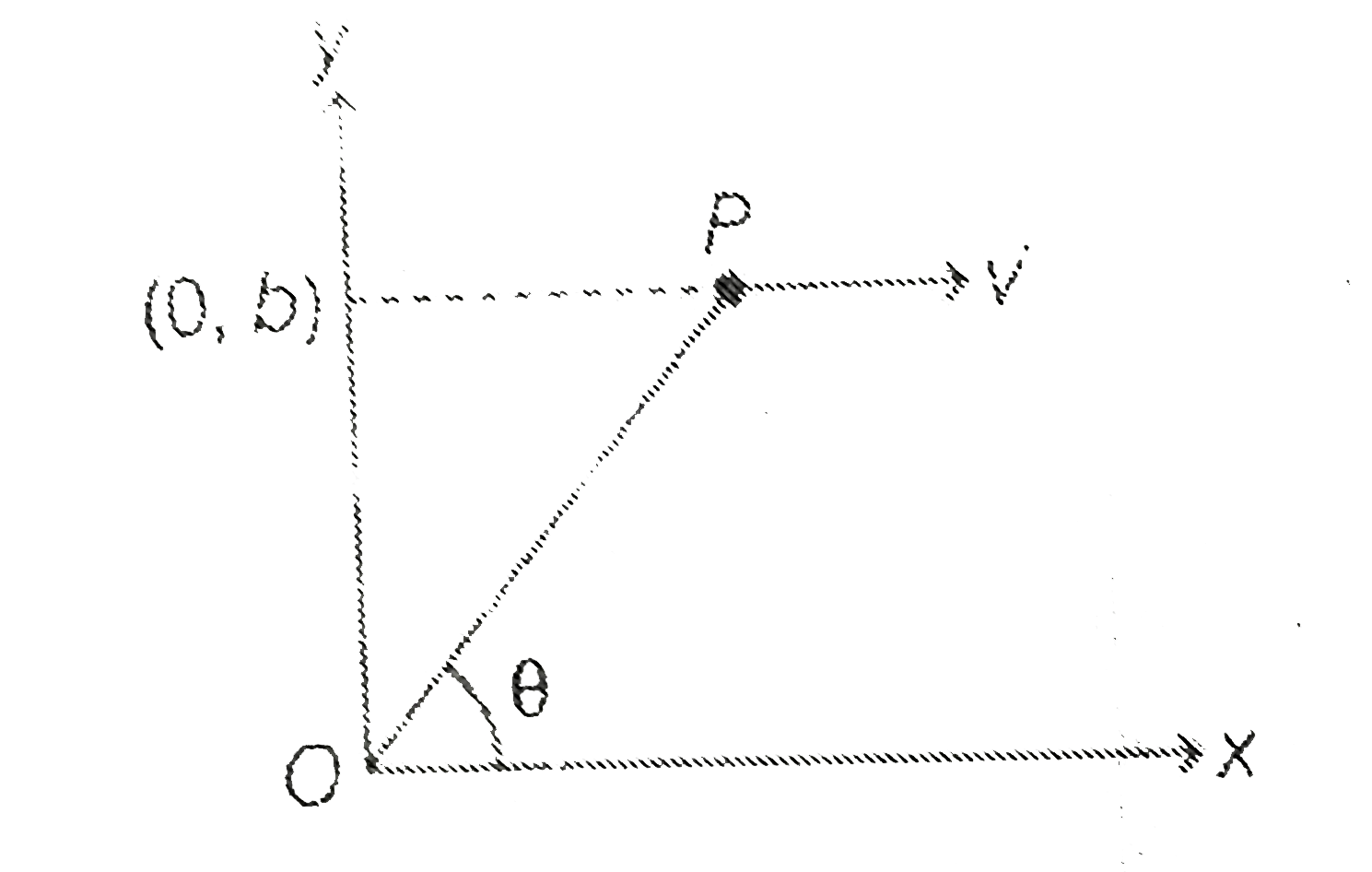
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA particle is moving in x-y plane as shown in the figure. Angular velocity of the particle with respect to the origin is
View SolutionVelocity of particle parallel to y- axis is
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is

View SolutionA particle moves in the plane xy with constant acceleration 'a' directed along the negative y-axis. The equation of motion of the particle has the form y=px−qx2 where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
View SolutionA particle moves in the plane xy with constant acceleration 'a' directed along the negative y-axis. The equation of motion of the particle has the form y=px−qx2 where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
View SolutionA particle has a linear momentum p and position vector r. the angular momentum of this particle about the origin will not be zero under the conditions
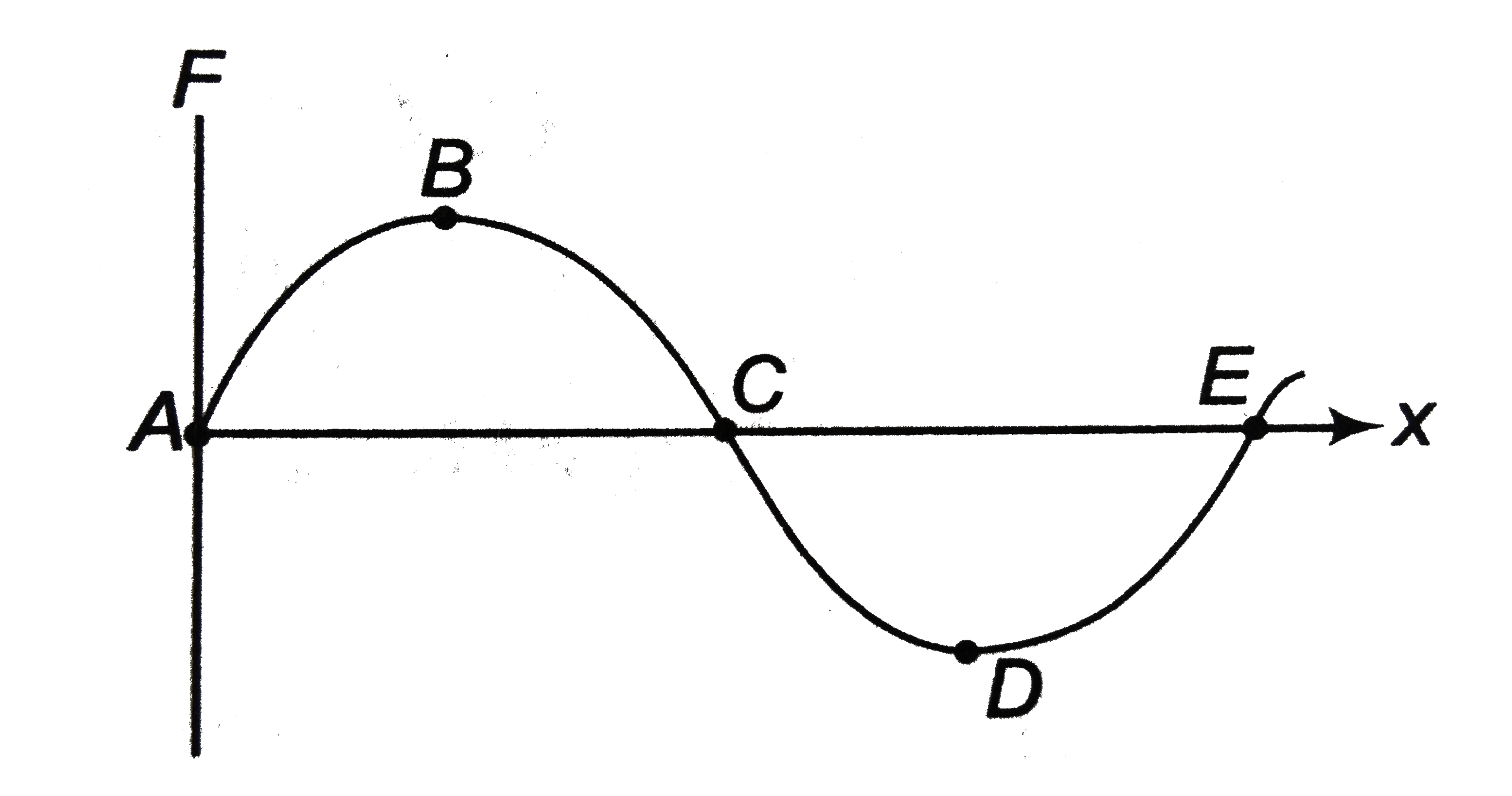
View SolutionForce acting on a particle moving along x-axis as shown in figure. Find points of stable and unstable equlibrium.
 .
.
View Solution