Two moving particles P and Q are 10 m apart at any instant. Velocity of P is 8 m/s at 30∘, from line joining the P and Q. Velocity of Q is 6 m/s at 30∘.Calculate the angular velocity of P with respect to Q.

ωPQ=8sin30∘−(−6sin30∘)10=0.7rad/s
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
8 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - Dynamics of circular motion
6 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Video
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
Two moving particles P and Q are 10cm apart at any instant. Velocity of P is 8m/s at 30∘, from line joining the P and Q and velocity of Q is 6m/s at 30∘. Calculate the angular velocity of P w.r.t. Q
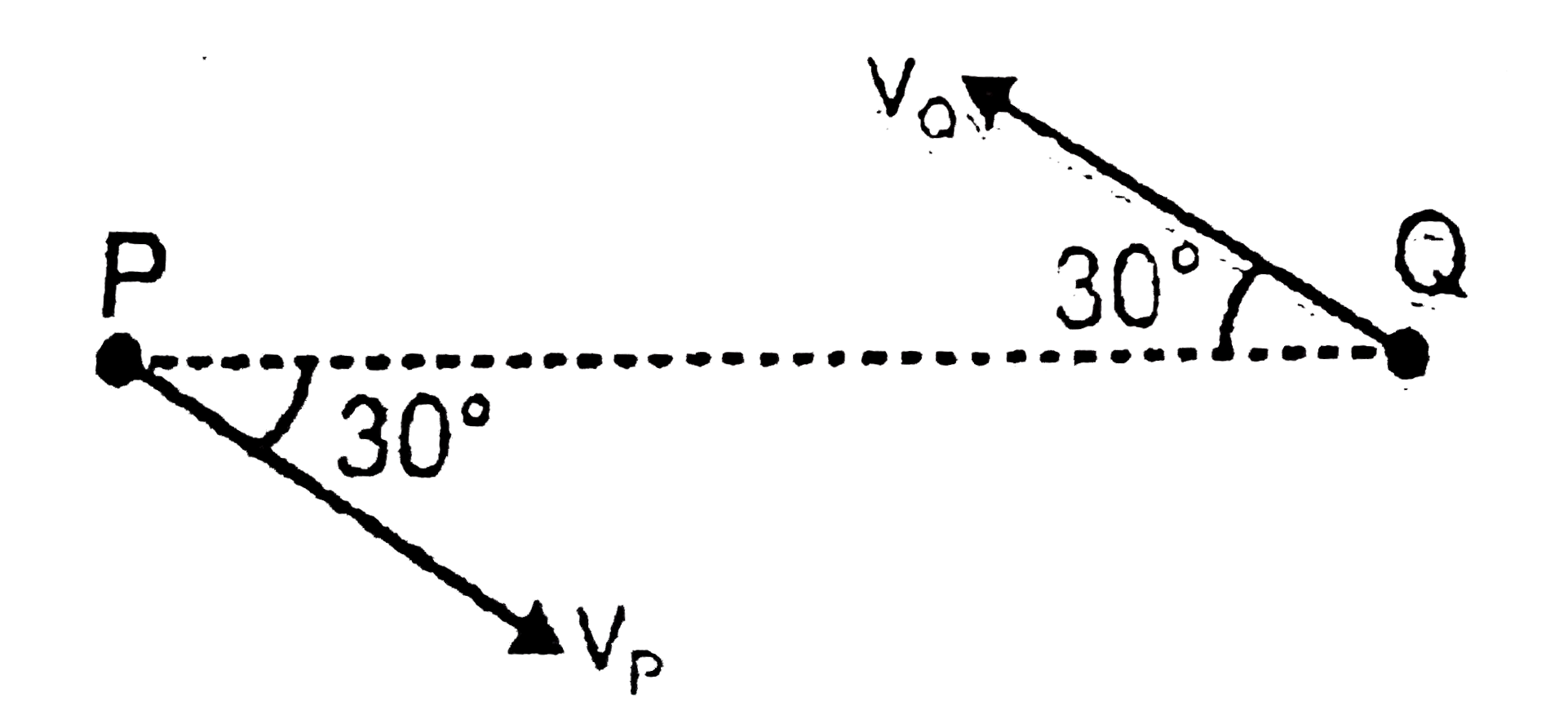
View Solution
Q. Species P and S are respectively:
View SolutionTwo particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
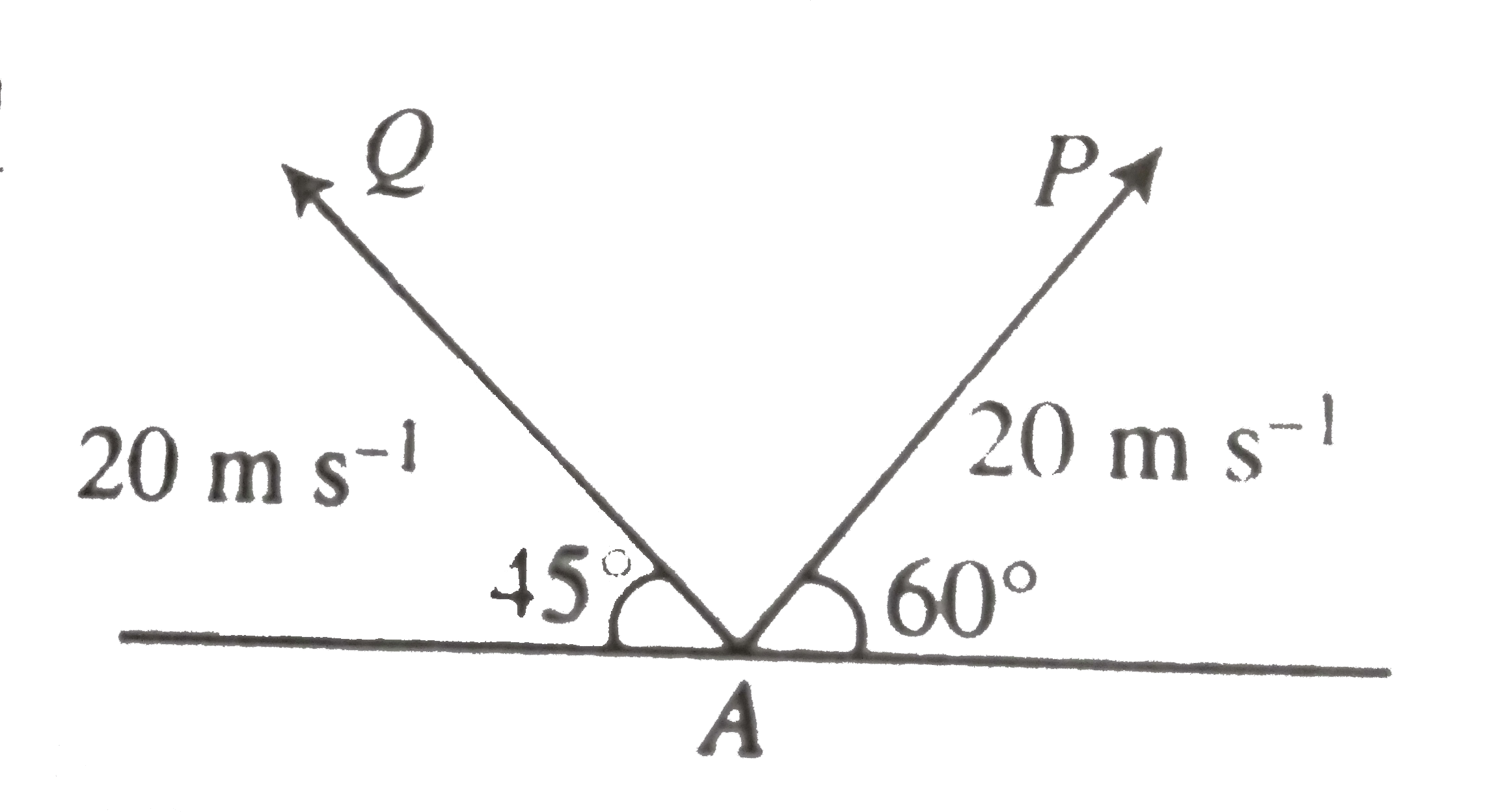
View SolutionTwo particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
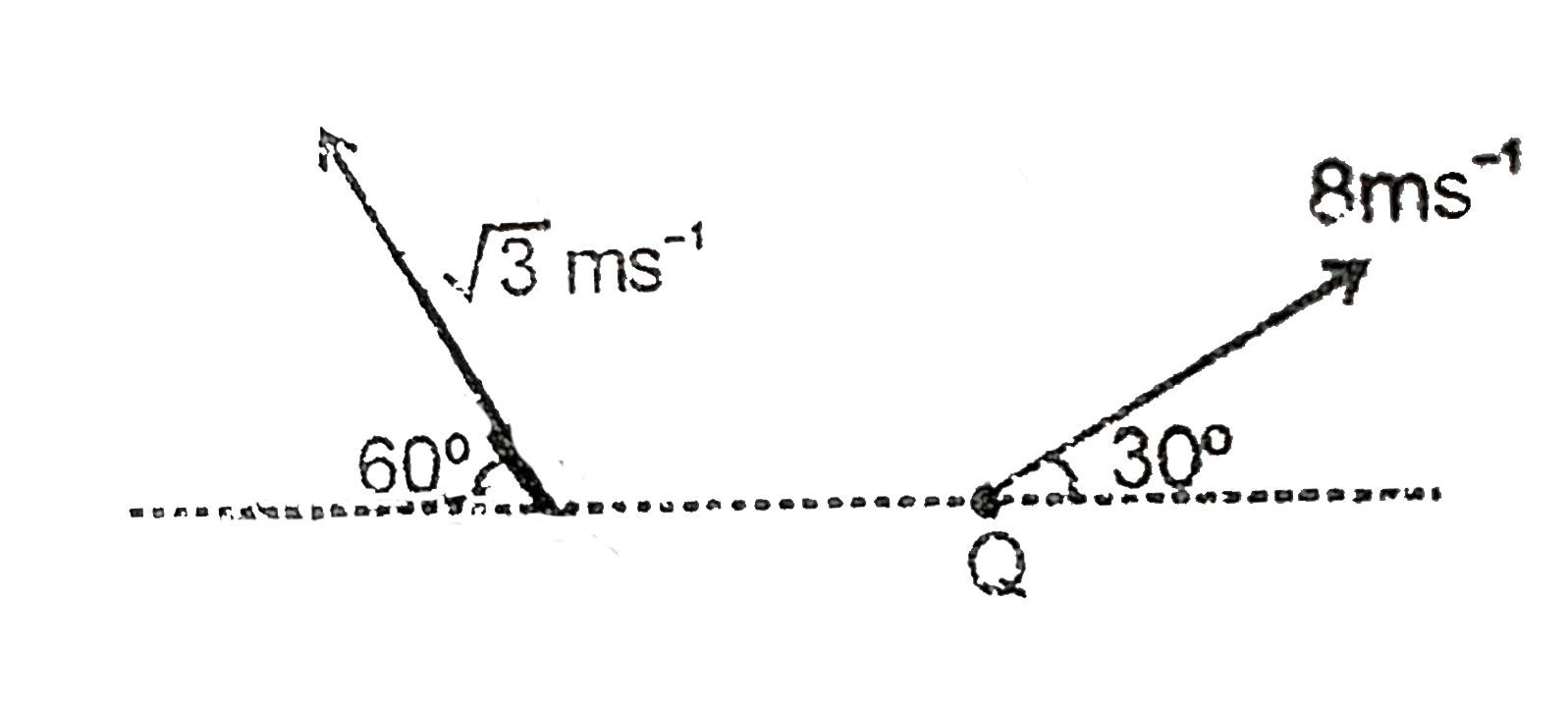
View SolutionTwo particles P and Q are moving on circle. At a certain instant of time both the particles and diametrically opposite and P has tangential acceleration 8m/s2 and centripetal acceleration 5m/s2 whereas Q has only e centripetal acceleration of1m/s2. At that instant acceleration (inm/s2) of P with respect to Q is
View SolutionThe displacement-time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities VP and VQ will be
View SolutionA two particles P and Q are separated by distance d apart. P and Q move with velocity v and u making an angle 60∘ and θ with line PQ the graph between their relative separation (8) when time t is shown in figure (2). The velocity v in terms of u
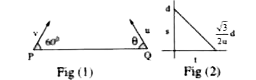
View SolutionA force P acts on a particle so as to accelerate it from rest to certain velocity. If P is replaced then by Q which decelerates it to rest.
View SolutionA sphere P of mass m moving with velocity u collides head on with another sphere Q of mass m which is at rest . The ratio of final velocity of Q to initial velocity of P is
( e = coefficient of restitution )
View SolutionTwo particles p and q located at distances rp and rq respectively from the centre of a rotating disc such that rp>rq.
View Solution
