An electron in the ground state of hydrogen atom is removing in unanticlockwise direction in a circle orbit of radius $R$

a. Obtain an expression for the orbital magnetic dipole moment of the electron .
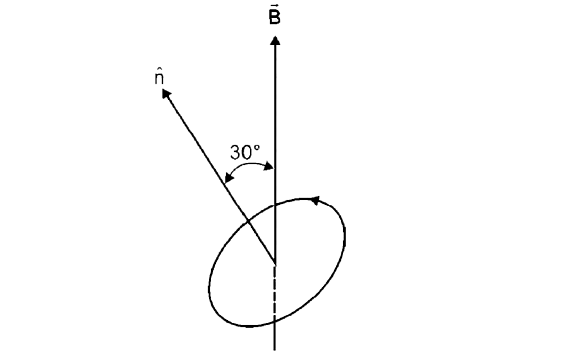
b. The atom is placed in a uniform magnetic indution $¯ ¯ ¯ B$ such that the plane normal to the electron orbitmakes an angle of $30^{\circ}$ with the magnetic induction. Find the tarque experienced by the orbiting electron .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(i) $\frac{h e}{4 π m}$ (ii) $\frac{e h B}{8 π m}$

(i) Magnetic moment $= I A = \frac{e h n}{4 π m}$
Produced is $n^{t h}$ orbit
for hydrogen $n = 1 \Rightarrow$ Magnetic moment $= \frac{e h}{4 π m}$
(ii) $\to τ = \to M \times \to B = \frac{e h}{4 π m} \times B \times {sin 30}^{\circ} = \frac{e h B}{8 π m}$

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
A $\frac{e h}{4 π m}$
B $\frac{e h}{2 π m}$
C $\frac{e h^{2}}{4 π m}$
D $\frac{e^{2} h}{4 π m}$
Question 2 - Select One
An electron moving in a circular orbit of radius r makes n rotations per second per second. The magnetic moment of the orbital electron is
Azero
B $π r^{2} n e$
C $π r^{2} n^{2} e$
D $\frac{r^{2} n e}{2 π}$

ALLEN-SIMPLE HARMONIC MOTION-Exercise - 04[A]

Home
Ask Doubt
Profile