A radioactive material of half-life T was produced in nuclear reactor at dirrent instants, the quantitiy produced second. Time was twic of that produced first time,If now their present acitivies are A1 and A2 respectively then their age difference equals
Tln2∣∣∣ln'A1A2∣∣∣
T∣∣∣ln'A1A2∣∣∣
TAln2∣∣∣ln'A22A1∣∣∣
T∣∣∣ln'A22A1∣∣∣
The correct Answer is:C
A1=λ−λ(t1−t2)⇒ln2A1A2=−λΔt⇒Δt=TlnA22A1ln2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 55
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 56
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 53
1 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A radioactive material of half-life T was kept in a nuclear reactor at two different instants. The quantity kept second time was twice of the kept first time. If now their present activities are A1 and A2 respectively, then their age difference equals
View SolutionA radioactive material of half-life T was kept in a nuclear reactor at two different instants. The quantity kept second time was twice of the kept first time. If now their present activities are A1 and A2 respectively, then their age difference equals
View Solution
Knowledge Check
A radioactive element X with half life 2 h decays giving a stable element Y. After a time t, ratio of X and Y atoms is 1:16 .Time t is
A6 hB4 hC8 hD16 h
A F32 radio nuclide with half-life T=14.3 days is produced in a reactor at a constant rate q=2×109 nuclei per second. How soon after the beginning of production of that radio nuclide will its activity be equal to R=109 disintegration per second?
View SolutionA radionuclide with half - life 1620 s is produced in a reactor at a constant rate of 1000 nuclei per second. During each decay energy, 200 MeV is released. If the production of radionuclides started at t = 0, then the rate of release of energy at t = 3240 s is
View SolutionFor a partiocular reaction with initial conc. Of the rectents as a1 and a2, the half-life period are t1 and t2 respectively. The order of the reaction (n) is given by :
View SolutionA radioactive with decay constant λ is being produced in a nuclear reactor at a rate q0t per second, where q0 is a positive constant and t is the time. During each decay, E0 energy is released. The production of radionuclide starts at time t=0.
Which differential equation correctly represents the above process?.
View SolutionA radioactive with decay constant λ is being produced in a nuclear ractor at a rate q0 per second, where q0 is a positive constant and t is the time. During each decay, E0 energy is released. The production of radionuclide starts at timet=0.
Average power developed in time t due to the decay of the radionuclide is
View SolutionA radioactive with decay constant λ is being produced in a nuclear ractor at a rate q0 per second, where q0 is a positive constant and t is the time. During each decay, E0 energy is released. The production of radionuclide starts at time t=0.
Instantaneous power developed at time t due to the decay of the radionuclide is .
View SolutionThe count rate of 10g of radioactive material was measured at different times and times has been shown in the figure. The half-life of material and the total counts (approximately) in the first half life period, respectively are.
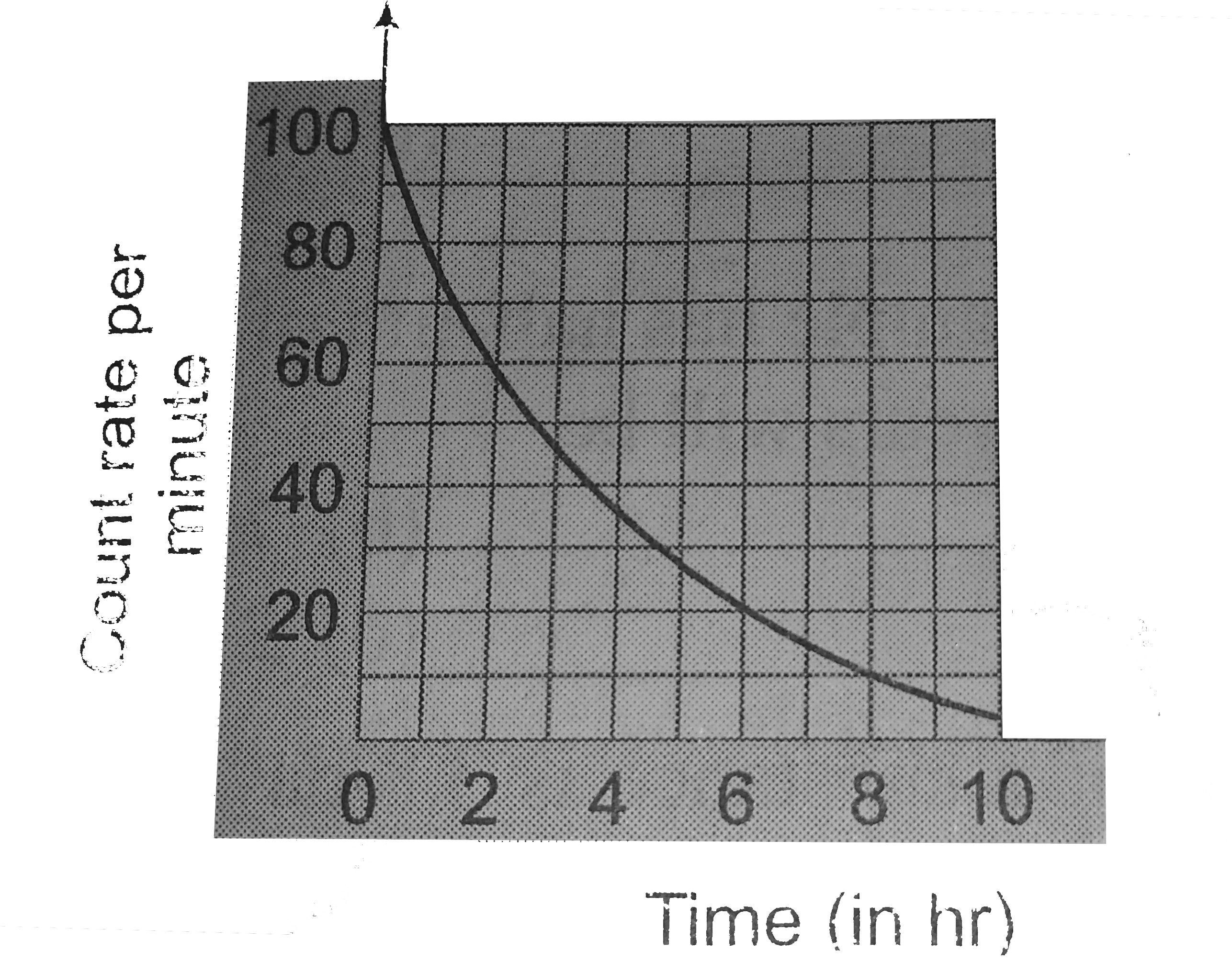 .
.
View Solution
