In a Coolidege tube experiment, the minimum wavelength of the continuouse X-ray spectrum is equal to 66.3 om . Then
electrons accelerate through a potential difference of 12.75kV in the Coolidge tube
electrons accelerate through a potential difference of 18.75kV in the Coolidge tube
de-Broglie wavelength of the electrons reaching the anticathode is of the order of 10pm
de-Broglie wavelength of the electrons reaching the anticathode is 0.01Å
The correct Answer is:B
To solve the problem regarding the Coolidge tube experiment and the minimum wavelength of the continuous X-ray spectrum, follow these steps:
1. Understand the Given Information:
- The minimum wavelength (λ₀) of the continuous X-ray spectrum is given as 66.3 picometers (pm).
- Convert this wavelength into meters for calculations:
λ₀=66.3pm=66.3×10−12m
2. Use the Formula for Minimum Wavelength:
- The formula relating minimum wavelength to the potential difference (Vₐ) in a Coolidge tube is:
λ₀ = \frac{hc}{eVₐ}
- Rearranging the formula to find the potential difference:
Vₐ=hceλ₀
3. Substitute the Constants:
- Use the following constants:
- Planck’s constant (h) = 6.626×10−34Js
- Speed of light (c) = 3.00×108m/s
- Charge of an electron (e) = 1.602×10−19C
4. Calculate the Potential Difference:
- Substitute the values into the equation:
Vₐ=(6.626×10−34Js)(3.00×108m/s)(1.602×10−19C)(66.3×10−12m)
- Calculate the numerator:
Numerator=6.626×10−34×3.00×108=1.9878×10−25Jm
- Calculate the denominator:
Denominator=1.602×10−19×66.3×10−12=1.063626×10−30C m
- Now, calculate Vₐ:
Vₐ=1.9878×10−251.063626×10−30≈18.75kV
5. Conclusion:
- The calculated potential difference Vₐ is approximately 18.75 kV, which matches the second option provided in the question.
- The minimum wavelength (λ₀) of the continuous X-ray spectrum is given as 66.3 picometers (pm).
- Convert this wavelength into meters for calculations:
λ₀=66.3pm=66.3×10−12m
- The formula relating minimum wavelength to the potential difference (Vₐ) in a Coolidge tube is:
λ₀ = \frac{hc}{eVₐ}
- Rearranging the formula to find the potential difference:
Vₐ=hceλ₀
- Use the following constants:
- Planck’s constant (h) = 6.626×10−34Js
- Speed of light (c) = 3.00×108m/s
- Charge of an electron (e) = 1.602×10−19C
- Substitute the values into the equation:
Vₐ=(6.626×10−34Js)(3.00×108m/s)(1.602×10−19C)(66.3×10−12m)
- Calculate the numerator:
Numerator=6.626×10−34×3.00×108=1.9878×10−25Jm
- Calculate the denominator:
Denominator=1.602×10−19×66.3×10−12=1.063626×10−30C m
- Now, calculate Vₐ:
Vₐ=1.9878×10−251.063626×10−30≈18.75kV
- The calculated potential difference Vₐ is approximately 18.75 kV, which matches the second option provided in the question.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise - 29
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise - 30
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise - 27
Explore 2 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
The nature of X-rays spectrum is
View SolutionThe minimum wavelength λmin in the continuous spectrum of X-rays is
View Solutionfind the minimum wavelength of the emitted X rays, when an X-ray tube is operated at 50 kV.
View SolutionIn the Coolidge tube experiment, if the applied voltage is increased to three times, the short wavelength limit of continuous X- ray spectrum shift by 20 pm. What is the initial voltage (in kV) applied to the tube?
View SolutionAn X-ray tube is operated at 50 kV. The minimum wavelength produced is
View SolutionFigure below shows a simple diagram of a modern X ray tube. (i.e. Coolidge tube).
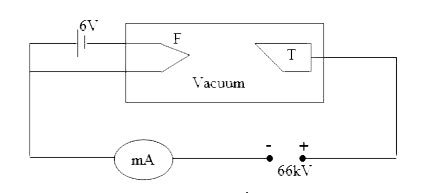
(i) Find the minimum wavelength of the X rays emitted by the X ray tube.
(ii) What will be the effect of replacing the 6V battery with a 9V battery on the emitted X rays?
View SolutionFind the cutoff wavelength for the continuous X-rays coming form an X-ray tube operating at 30 kV.
View SolutionConsider the following two statements A and B and identify the correct choice in the given answer
A : The characteristic X-ray spectrum depends on the nature of the material of the target
B : The short wavelength limit of continuous X-ray spectrum varies inversely with the potential difference applied to the X-rays tube
View SolutionIn an X-rays tube, electrons striking a target are brought to rest, causing X-rays to be emitted. In a paricular X-ray tube, the maximum frequency of the emitted continuum X-ray spectrum is fo. If the votage across the tube is doubled, the maximum frequency is
View SolutionFind the cut off wavelength for the continuous X - rays coming from an X-ray tube operating at 40 kV.
View Solution

