A very light rod of length l pivoted at O is connected with two springs of stiffness k1 & k2 at a distance of a & l from the pivot respectively. A block of mass ma attached with the spring k2 is kept on a smooth horizontal surface. Find the angular frequency of small oscillation of the block m.
_S01_031_Q01.png)
Let the block be pulled towards right through a distance x, then x=xB+xCB…..(i)
where, xCH= displacement of C (the block) relative to B
Thus, xCB=Fk2….(ii) and xB=(F'k1)la
Torque acting on the rod about point O.
τ0=F'a−Fl⇒I0d2θdt2=F'a−Fl
Since the rod is very light its moment of inertia
I0 about O is approximentely equal to zero ⇒F'=F(la).....(iv)
Using (iii) and (iv) ⇒xB=Fk1(la)2.............
Using (i), (ii) & (v) ⇒x=Fk1(la)2+Fk2
As force F is opposite to displacement x, then
⇒F=−k1k2k2(la)2+k1x⇒mω2x=k1k2k2(la)2+k1x⇒ω=√k1k2a2m(k1a2+k2l2)
_S01_031_S01.png)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:SOME WORKED OUT EXAMPLES
Explore 29 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

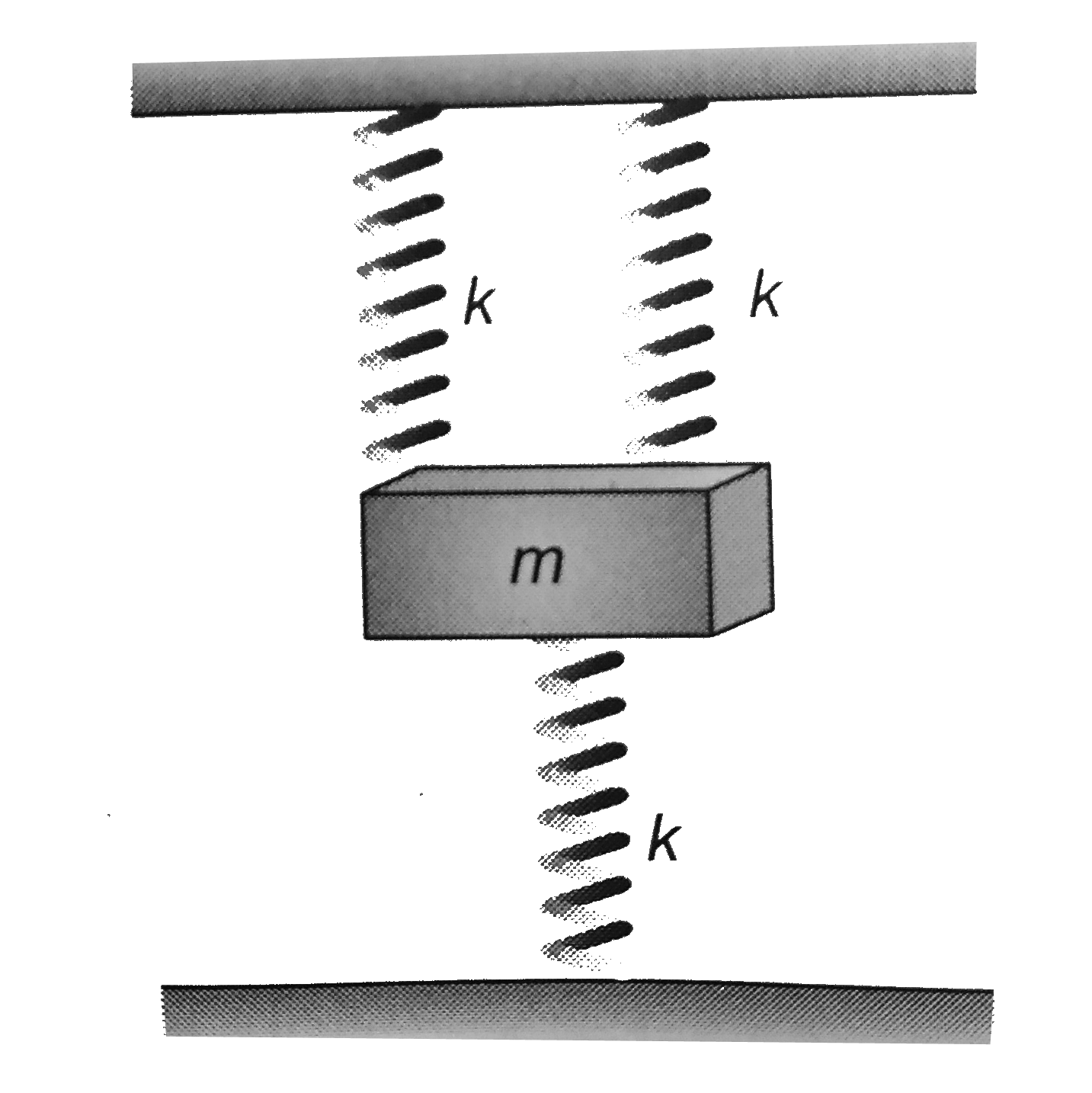
View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
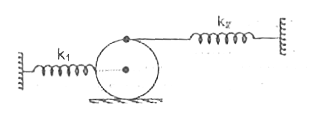
View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
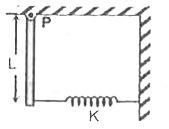
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View Solution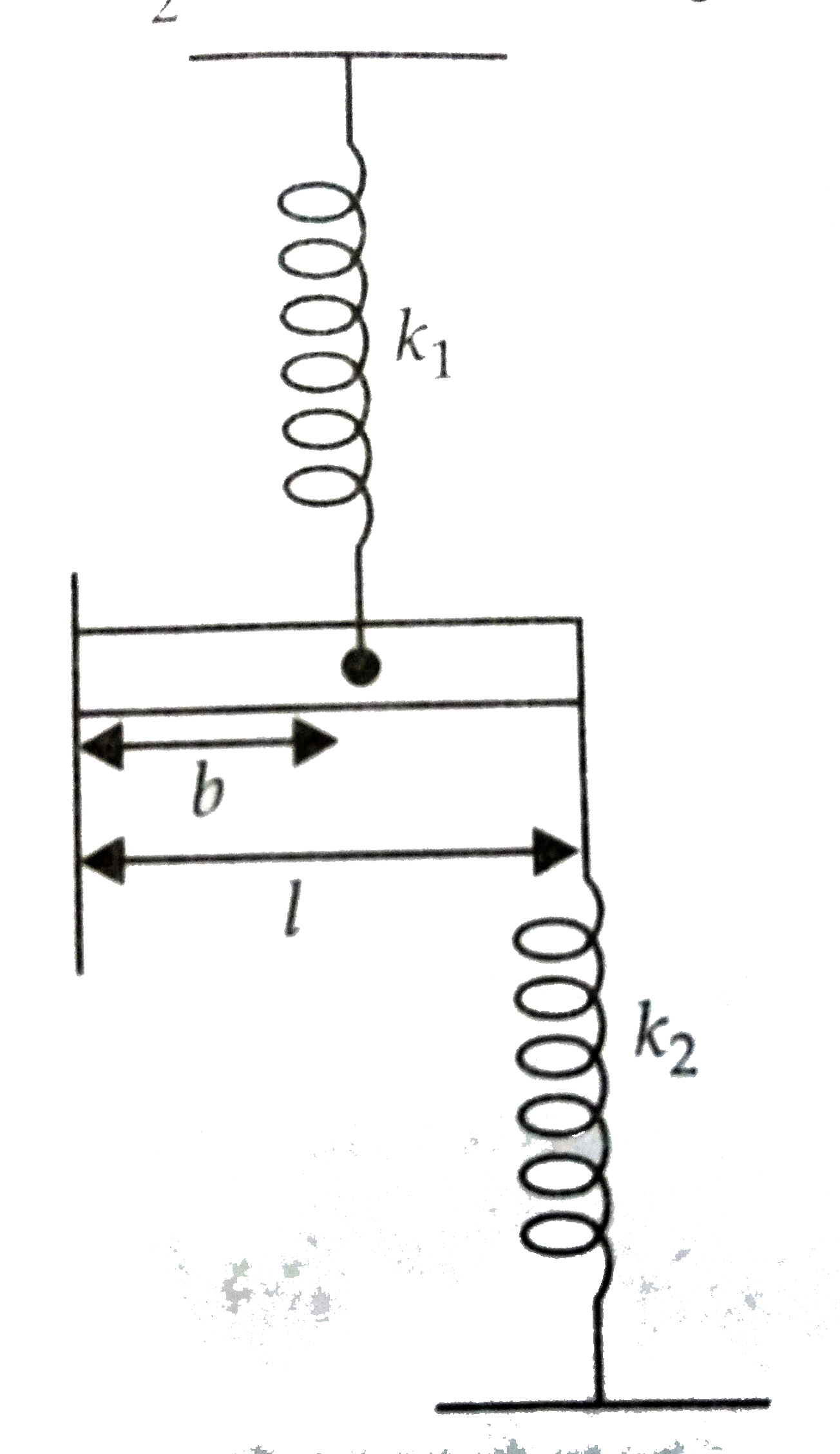
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View Solution

