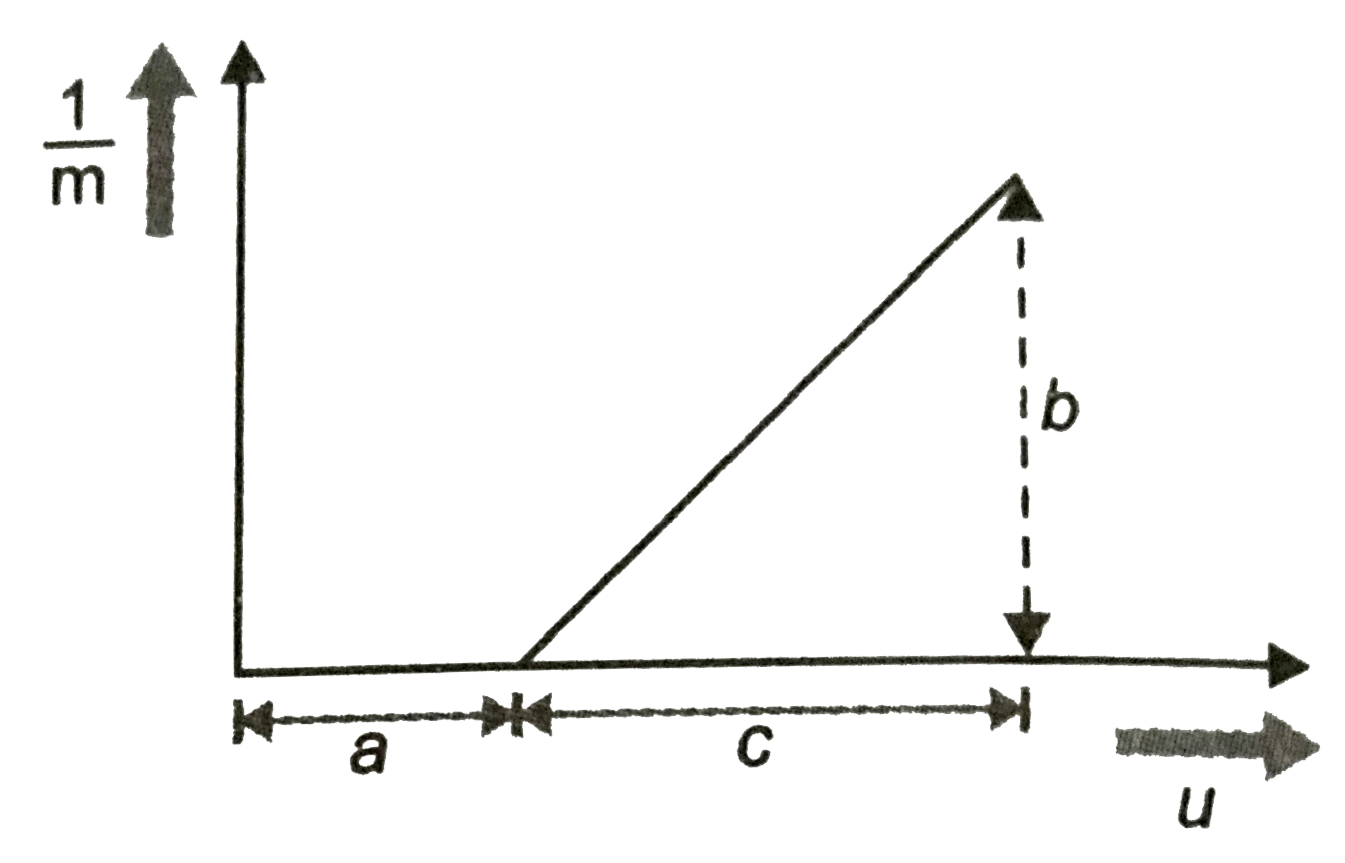
Consider the following diagram representing magnitude of magnification against image distance for a convex lens:
_E01_094_Q01.png)
Column IColumn II(A)Focal length of the lens(p)Inverse of slope of line(B)Intercept on x- axis(q)Unity(C)Intercept on y-axis(r)Focal length(D)Magnitude of slope of the line(s)(s)Inverse of the focal length
The correct Answer is:(A)-p (B)-r (C)-q (D)-s
m=v−ff=vf−1(∴y=mx+c)
m = slope = 1f (magnitude of slope of line)
Intercet on y axis c =-1 (unity)
Intercet on x-axis ⇒m=0
⇒0=vf−1⇒v=f(focal length)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]
23 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[B]
18 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-2
44 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Column - II shows the optical phenomenon that can be associated with optical components given in column- I . Note the column - I may have more than one matching options in column-II.
Column IColumn II(A)Convex mirror(p)Dispersion(B)Converging lens(q)Deviation(C)Thin prism(r)Real image of real object(D)Glass slab(s)Virtual images of real object
View SolutionMatch the column I with column II
Column-IColumn-II(A)Fructose(p)Protein(B)Zwitterion(q)Inversion(C)Peptide linkage(r)α−Amino acid(D)Hydrlysis of cane sugar(s)Carbohydroate(t)Ketose
View SolutionMatch the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)d v/dt(p)Acceleration(B)d|v|/dt(q)Magnitude of acceleration(C)drdt(r)Velocity(D)∣∣drdt∣∣(s)Magnitude of velocity(t)Rate of change of speed∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionThe graph in Fig. shows how the inverse of magnification 1/m produced by a convex thin lens varies with object distance u. What was the focal length of the lens used ?
 .
.
View SolutionWhen an object is at distances x and y from a lens, a real image and a virtual image is formed respectively having same magnification. The focal length of the lens is
View SolutionAn object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of 5m/s the speed and direction of the image will be :
View SolutionDraw ray diagrams showing the image formation by a convex lens when an object is placed
(a) between optical centre and focus of the lens
(b) between focus and twice the focal length of the lens
( c) at twice the focal length of the lens
(d) at infinity , (e) at the focus of the lens
View Solution(i) A diverging lens of focal length 15 cm, forms an image at distance of 10 cm from the lens. How far is the object placed from the lens ?
(ii) What is the linear magnification of the image?
View SolutionColumn I (optical system )
_S01_024_Q01.png)
Column II (focal length )
(P)80cm (Q)40cm (R)30cm (S)20cm
View SolutionColumn IColumn II(A) An object is placed at a distance equal to focal length from pole before convex mirror(p) Magnification is (∞)(B) An object is placed at focus before a concave mirror(q) Magnification is (0.5)(C)An object is placed at the centre of curvature before a concave mirror(r)Magnification is (1//3)(D) An object is placed at a distance equal to radius of curvature before a convex mirror(s)Magnification is (-1)
View Solution
