A vertical cylinder of cross-sectional area 0.1m2 closed at both ends is fitted with a frictionless piston of mass M dividing the cylinder into two parts. Each part contains one mole of an ideal gas in equilibrium at 300K. The volume of the upper part is 0.1m3 and that of lower part is 0.05m3 .What force must be applied to the piston so that the volumes of the two parts remain unchanged when the temperature is increased to 500K?
The correct Answer is:1660N
To solve the problem, we need to determine the force that must be applied to the piston to keep the volumes of the two parts of the cylinder unchanged when the temperature is increased from 300K to 500K. We will use the ideal gas law and the relationship between pressure, volume, and temperature.
1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where P is the pressure, V is the volume, n is the number of moles, R is the universal gas constant, and T is the temperature in Kelvin.
2. Calculate Initial Pressures:
For the upper part of the cylinder (volume V1=0.1m3):
P1=nRT1V1=1×R×3000.1
For the lower part of the cylinder (volume V2=0.05m3):
P2=nRT2V2=1×R×3000.05
3. Calculate the Change in Pressure:
The net force on the piston is given by the difference in pressure multiplied by the area A:
Fnet=(P1−P2)×A
The cross-sectional area A is given as 0.1m2.
4. Calculate New Pressures at Higher Temperature:
When the temperature is increased to 500K:
P′1=nRT′1V1=1×R×5000.1
P′2=nRT′2V2=1×R×5000.05
5. Calculate the New Net Force:
The new net force on the piston when the temperature is increased:
F′net=(P′1−P′2)×A
6. Determine the Force Required to Maintain Volume:
The force that must be applied to the piston to keep the volumes unchanged is the difference in the forces due to the change in pressure:
Fapplied=F′net−Fnet
7. Substituting Values:
Substitute the values of P1, P2, P′1, and P′2 into the equations to find the required force.
8. Final Calculation:
After calculating the above values, we find that the force required to maintain the volume unchanged when the temperature is increased to 500K is:
Fapplied=nRΔTV=1×253×2000.1=50003N
Final Answer:
The force that must be applied to the piston is 50003N.
The ideal gas law is given by the equation:
PV=nRT
where P is the pressure, V is the volume, n is the number of moles, R is the universal gas constant, and T is the temperature in Kelvin.
For the upper part of the cylinder (volume V1=0.1m3):
P1=nRT1V1=1×R×3000.1
For the lower part of the cylinder (volume V2=0.05m3):
P2=nRT2V2=1×R×3000.05
The net force on the piston is given by the difference in pressure multiplied by the area A:
Fnet=(P1−P2)×A
The cross-sectional area A is given as 0.1m2.
When the temperature is increased to 500K:
P′1=nRT′1V1=1×R×5000.1
P′2=nRT′2V2=1×R×5000.05
The new net force on the piston when the temperature is increased:
F′net=(P′1−P′2)×A
The force that must be applied to the piston to keep the volumes unchanged is the difference in the forces due to the change in pressure:
Fapplied=F′net−Fnet
Substitute the values of P1, P2, P′1, and P′2 into the equations to find the required force.
After calculating the above values, we find that the force required to maintain the volume unchanged when the temperature is increased to 500K is:
Fapplied=nRΔTV=1×253×2000.1=50003N
The force that must be applied to the piston is 50003N.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A vertical cylinder closed at both ends is fitted with a smooth piston dividing the volume into two parts each containing one mole of air. At the equilibrium temperature of 320 K, the volume of upper and lower parts are in the ratio 4:1. The ratio of volume will become 3:1 at a temperature of
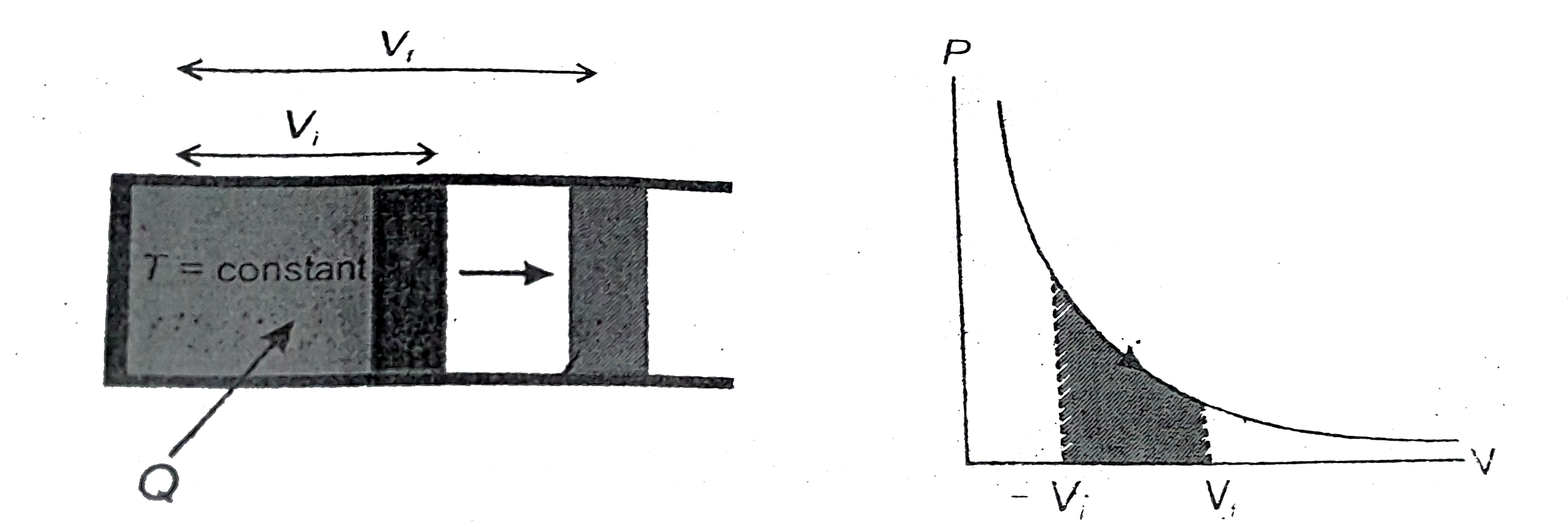
View SolutionA cylinder contains 0.50 mol of an ideal gas at temperature of 310 K. as the gas expands isothermally from an initial volume of 0.31 m3 to a final volume of 0.45m3, find the amount of heat that must be added to the gas in order to maintain a constant temperature.
View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionA piston can freely move inside a horizontal cylinder closed from both ends. Initially, the piston separates the inside space of the cylinder into two equal parts each of volume V0 in which an ideal gas is contained under the same pressure p0 and at the same temperature. What work has to be performed in order to increase isothermally the volume of one part of gas η times compared to that of the other by slowly moving the piston ?
View SolutionA container of volume 1m3 is divided into two equal parts by a partition. One part has an ideal gas at 300K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be .......
View SolutionA container of volume 1m3 is divided into two equal parts by a partition. One part has an ideal gas at 300K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be .......
View SolutionA closed gas cylinder is divided into two parts by a piston held tight. The pressure and volume of gas in two parts respectively are (P, 5V) and (10P, V). If now the piston is left free and the system undergoes isothermal process, then the volumes of the gas in two parts respectively are
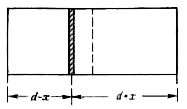
View SolutionA piston of mass m divides a cylinder containing gas into two equal parts. Suppose the piston is displaced to the left to a distance x and let go Fig. Assuming the process to take place at a constant temperature, find the frequency of the piston's oscillations.
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View Solution
