A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals v0, then th speed of the particle as a function of the distance covered S will be
v=v0e−S/R
v=v0eS/R
v=v0e−R/S
v=v0eR/S
The correct Answer is:A
To solve the problem, we need to find the speed of a particle moving in a circular path as a function of the distance covered, given that its tangential and normal accelerations are equal in magnitude.
1. Understanding the Problem:
- The particle moves in a circular path with radius R.
- At any moment, the tangential acceleration at and the normal (centripetal) acceleration an are equal in magnitude.
- The initial speed of the particle at t=0 is v0.
2. Define the Accelerations:
- The tangential acceleration at is given by:
at=dvdt
- The normal acceleration an (centripetal acceleration) is given by:
an=v2R
3. Setting Up the Equation:
- Since the magnitudes of the tangential and normal accelerations are equal, we can write:
dvdt=v2R
4. Changing Variables:
- We want to express v as a function of the distance s covered by the particle. We can use the chain rule:
dvdt=dvds⋅dsdt
- Here, dsdt=v, hence:
dvdt=dvds⋅v
5. Substituting into the Equation:
- Substitute dvdt into the equation:
dvds⋅v=v2R
- Dividing both sides by v (assuming v≠0):
dvds=vR
6. Separating Variables:
- Rearranging gives:
1vdv=1Rds
7. Integrating Both Sides:
- Integrate both sides:
∫1vdv=∫1Rds
- This results in:
ln|v|=sR+C
- Where C is the constant of integration.
8. Applying Initial Conditions:
- At s=0, v=v0:
ln|v0|=C
- Thus, the equation becomes:
ln|v|=sR+ln|v0|
9. Exponentiating Both Sides:
- Exponentiating gives:
|v|=|v0|esR
- Since speed cannot be negative, we can drop the absolute value:
v=v0esR
10. Final Expression:
- The speed of the particle as a function of the distance covered s is:
v=v0e−sR
Final Answer:
v=v0e−sR
- The particle moves in a circular path with radius R.
- At any moment, the tangential acceleration at and the normal (centripetal) acceleration an are equal in magnitude.
- The initial speed of the particle at t=0 is v0.
- The tangential acceleration at is given by:
at=dvdt
- The normal acceleration an (centripetal acceleration) is given by:
an=v2R
- Since the magnitudes of the tangential and normal accelerations are equal, we can write:
dvdt=v2R
- We want to express v as a function of the distance s covered by the particle. We can use the chain rule:
dvdt=dvds⋅dsdt
- Here, dsdt=v, hence:
dvdt=dvds⋅v
- Substitute dvdt into the equation:
dvds⋅v=v2R
- Dividing both sides by v (assuming v≠0):
dvds=vR
- Rearranging gives:
1vdv=1Rds
- Integrate both sides:
∫1vdv=∫1Rds
- This results in:
ln|v|=sR+C
- Where C is the constant of integration.
- At s=0, v=v0:
ln|v0|=C
- Thus, the equation becomes:
ln|v|=sR+ln|v0|
- Exponentiating gives:
|v|=|v0|esR
- Since speed cannot be negative, we can drop the absolute value:
v=v0esR
- The speed of the particle as a function of the distance covered s is:
v=v0e−sR
v=v0e−sR
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Assertion-Reason
Explore 20 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-01
Explore 55 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
At freezing point of a solution there is always
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
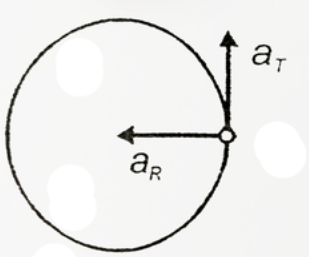
The time after which the speed of particle reduces to half of its initial value is
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
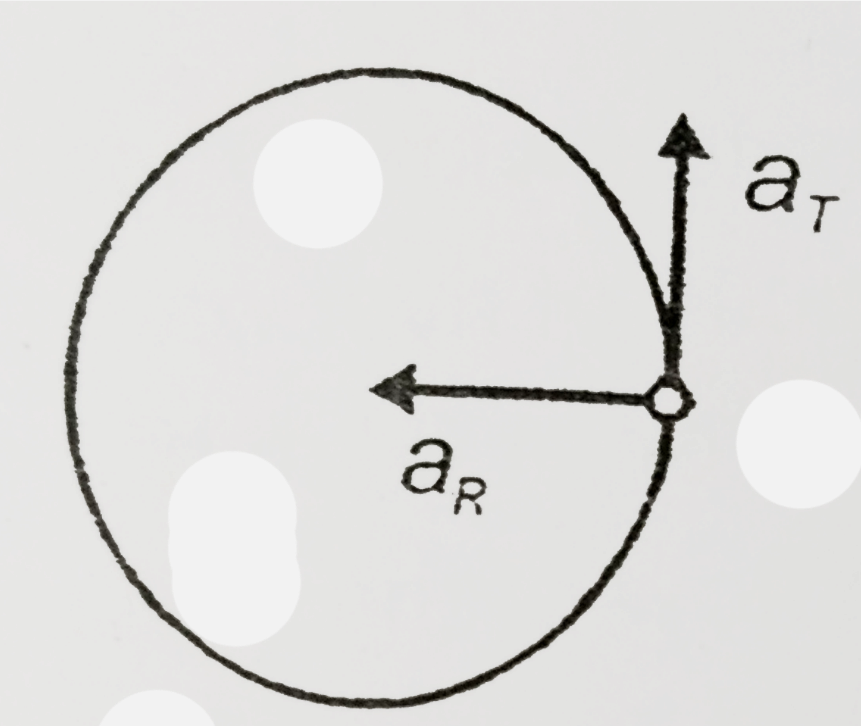
The magnitude of tangential acceleration at t=R2u is
View SolutionA particle is moving on a circle of radius R such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be v0 at t=0, the time for the completion of the half of the first revolution will be
View SolutionA particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential component of the acceleration are equal. If its speed at t=0 is u0 the time taken to complete the first revolution is
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
View SolutionAt any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
View Solution

