Which of the following pairs of graphs does not represent the motion of he same particle in the same interval (curves are parabollic):−
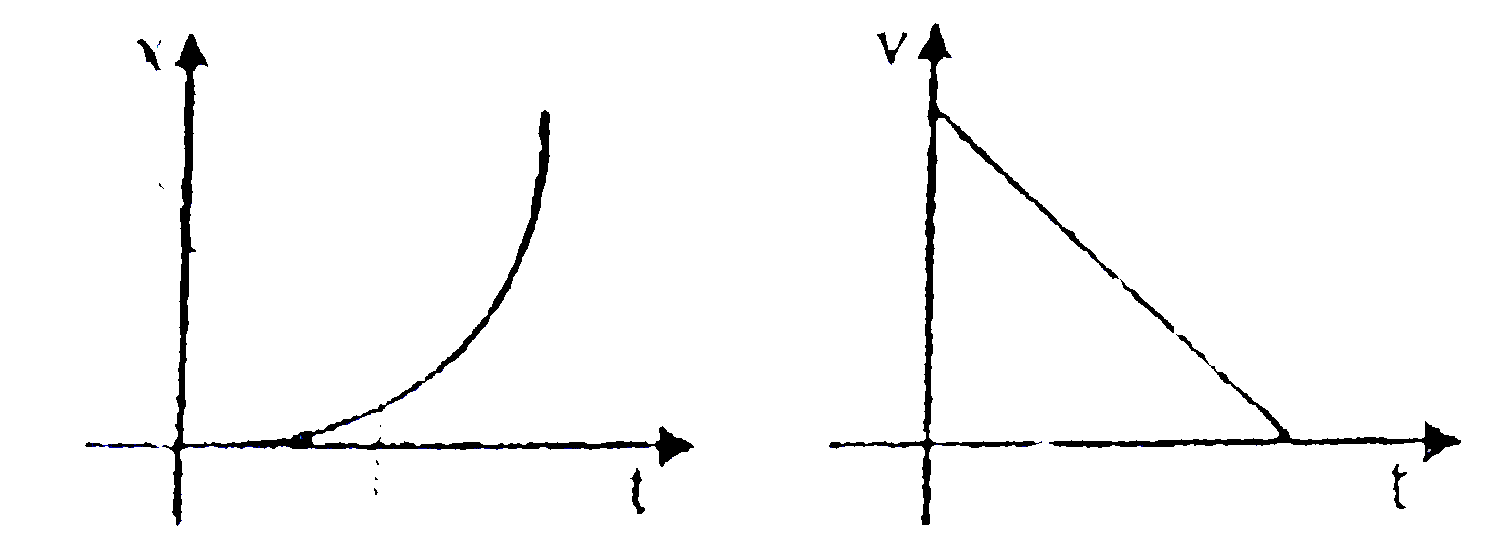
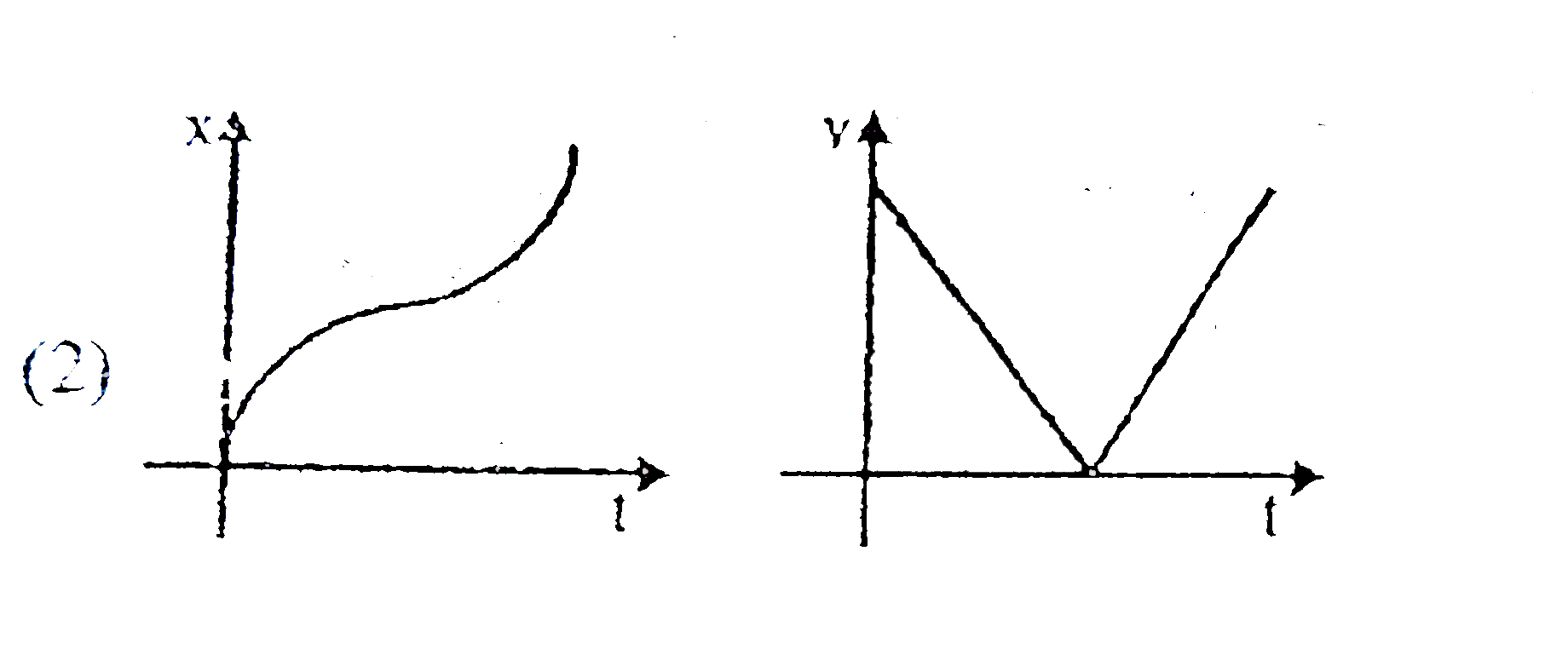

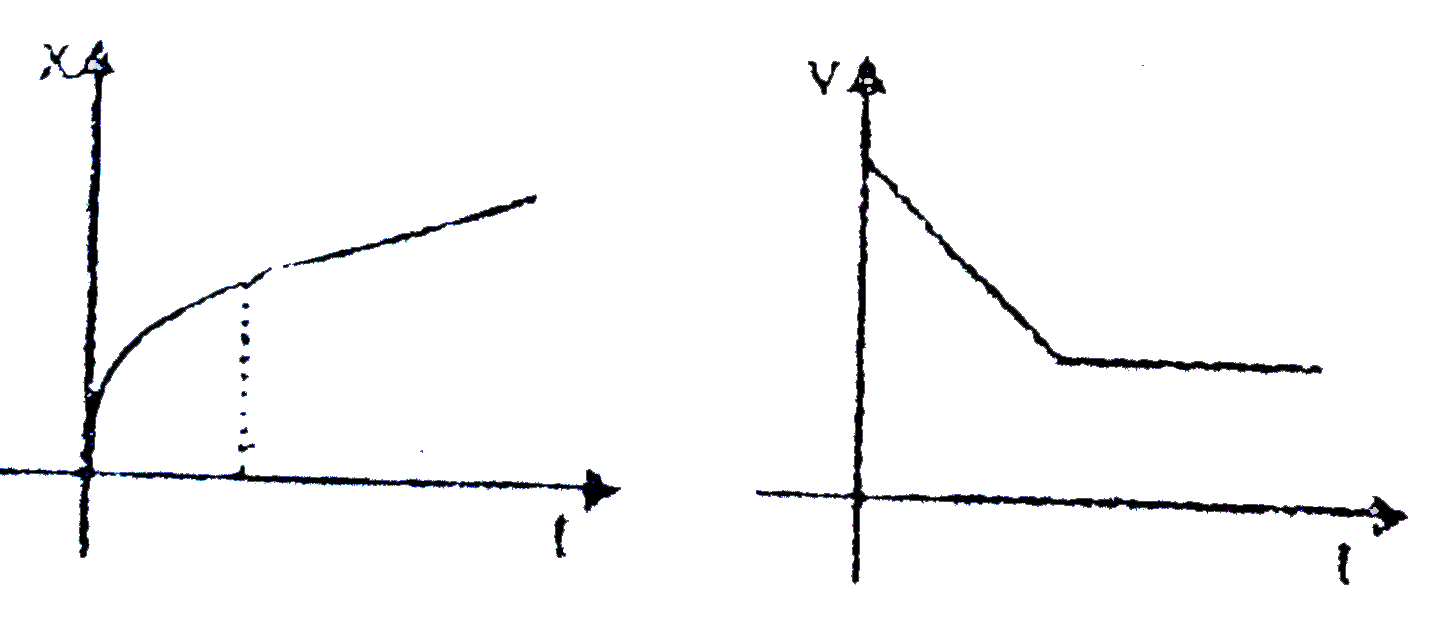
The correct Answer is:A
To determine which pair of graphs does not represent the motion of the same particle in the same interval, we need to analyze the displacement-time graphs and their corresponding velocity-time graphs.
1. Understanding Displacement-Time Graphs:
- The slope of a displacement-time graph represents the velocity of the particle.
- A positive slope indicates positive velocity, while a negative slope indicates negative velocity. A zero slope indicates that the particle is at rest.
2. Analyzing the Graphs:
- We will look at the initial and final slopes of the graphs to determine the velocities at those points.
- For the first graph, if the initial slope is non-zero (indicating initial velocity) and the final slope is zero (indicating the particle comes to rest), this is a valid representation of motion.
3. Comparing Pairs of Graphs:
- If we find a pair where one graph has an initial slope of zero and the other has a non-zero slope, they cannot represent the same particle's motion in the same interval.
- For instance, if one graph starts from rest (zero slope) and the other starts with some velocity (non-zero slope), they are inconsistent.
4. Checking for Acceleration:
- The acceleration can be determined from the curvature of the graphs. If the graph is concave up, the acceleration is positive, and if concave down, the acceleration is negative.
- We can also check the second derivative (the curvature) to confirm if the graphs are consistent with the expected motion.
5. Identifying the Incorrect Pair:
- After analyzing the slopes and curvatures, we find that one pair of graphs has inconsistent initial and final slopes. This indicates they do not represent the same particle's motion.
Conclusion:
The pair of graphs that does not represent the motion of the same particle in the same interval is the one where one graph has a zero initial slope while the other has a non-zero initial slope.
- The slope of a displacement-time graph represents the velocity of the particle.
- A positive slope indicates positive velocity, while a negative slope indicates negative velocity. A zero slope indicates that the particle is at rest.
- We will look at the initial and final slopes of the graphs to determine the velocities at those points.
- For the first graph, if the initial slope is non-zero (indicating initial velocity) and the final slope is zero (indicating the particle comes to rest), this is a valid representation of motion.
- If we find a pair where one graph has an initial slope of zero and the other has a non-zero slope, they cannot represent the same particle's motion in the same interval.
- For instance, if one graph starts from rest (zero slope) and the other starts with some velocity (non-zero slope), they are inconsistent.
- The acceleration can be determined from the curvature of the graphs. If the graph is concave up, the acceleration is positive, and if concave down, the acceleration is negative.
- We can also check the second derivative (the curvature) to confirm if the graphs are consistent with the expected motion.
- After analyzing the slopes and curvatures, we find that one pair of graphs has inconsistent initial and final slopes. This indicates they do not represent the same particle's motion.
The pair of graphs that does not represent the motion of the same particle in the same interval is the one where one graph has a zero initial slope while the other has a non-zero initial slope.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - Exercise (Physics)330videos
TEST PAPER
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS11videos
TEST PAPER 1
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following x-t graphs does not represent periodic motion?
A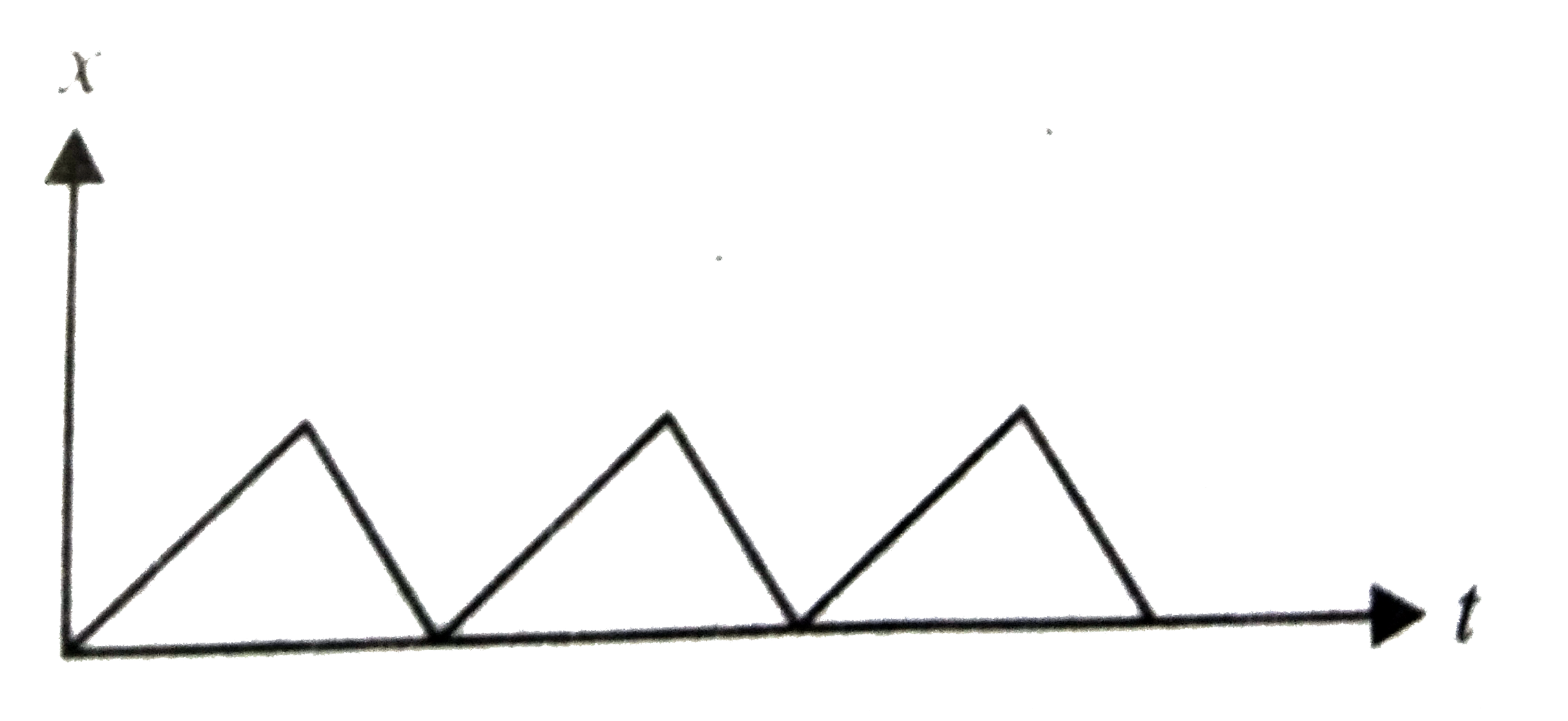 B
B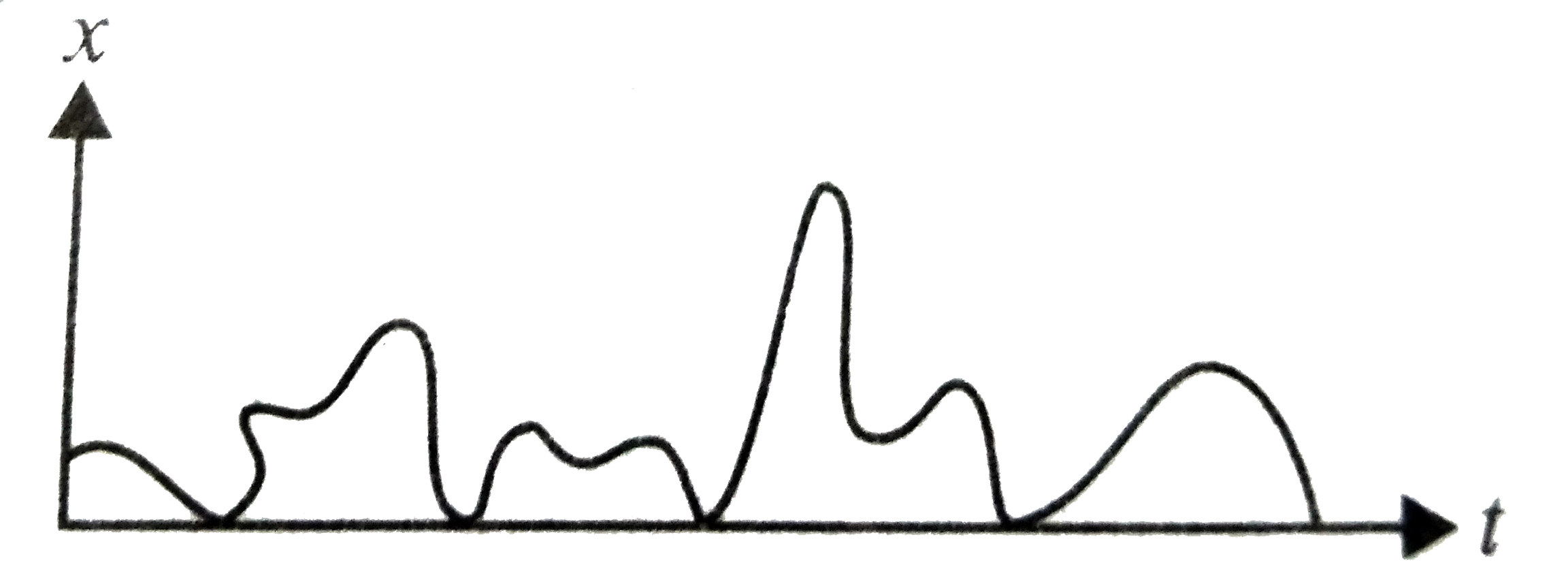 C
C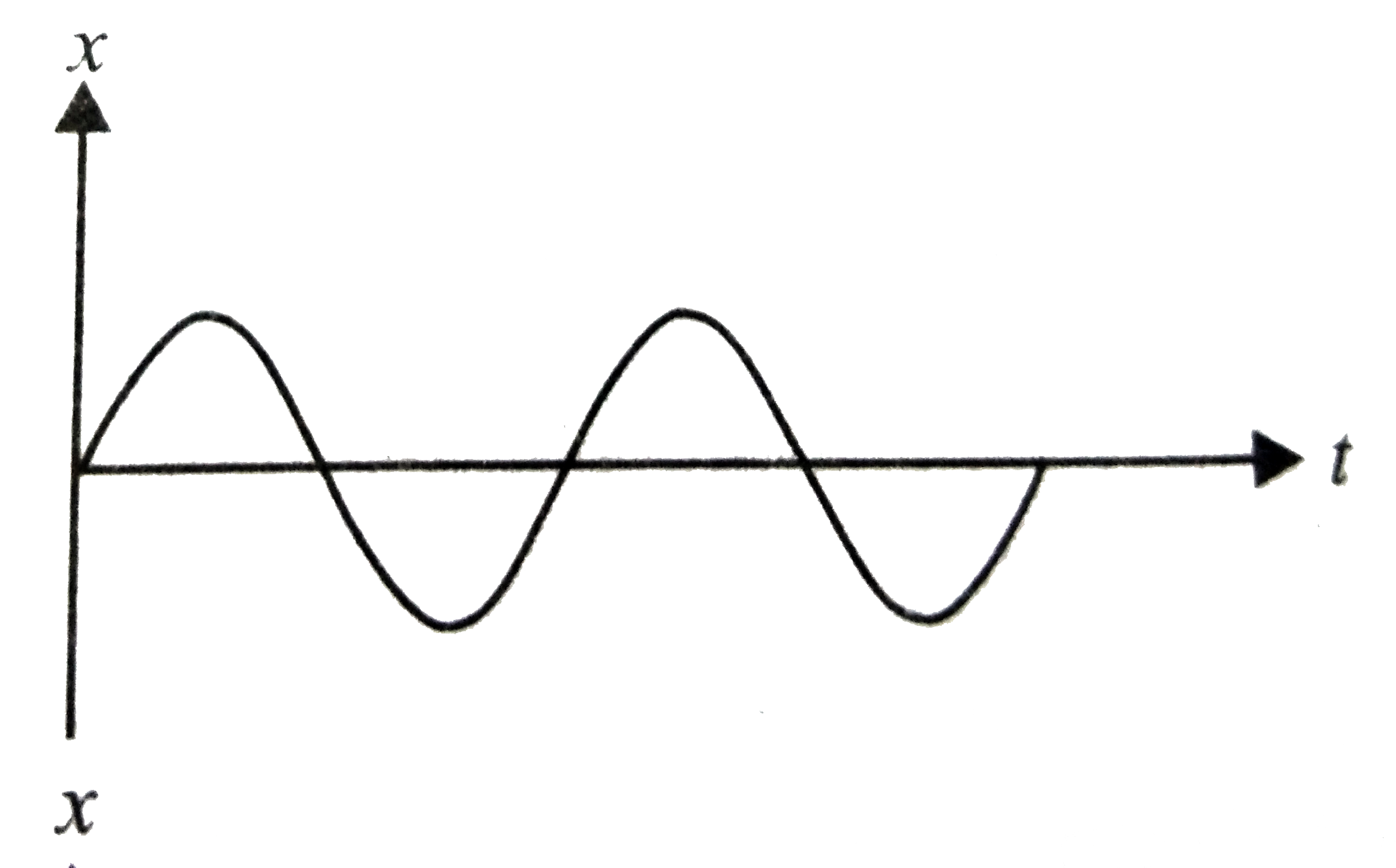 D
D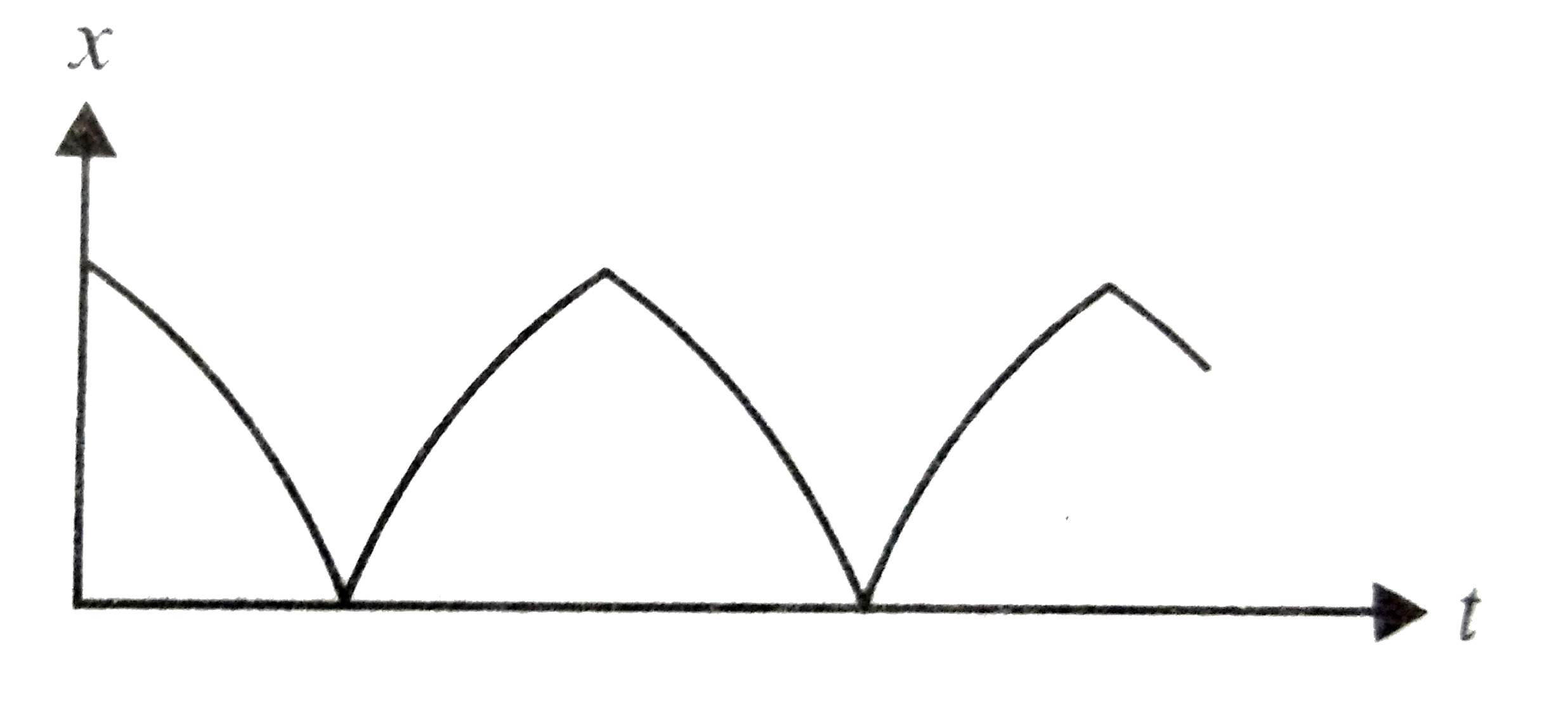
- Question 2 - Select One
Which of the following pairs of structures does not represent isomers?
A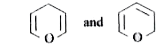 B
B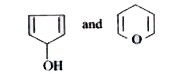 C
C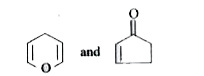 D
D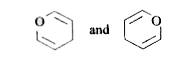
- Question 3 - Select One
Which of the following pairs of structures does not represent isomers?
A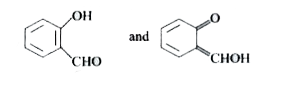 B
B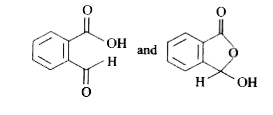 C
C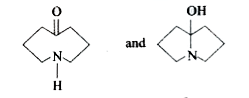 D
D
Which of the following are extensive properties ?
View SolutionWhich of the following graphs represents the motion of a particle moving with constant velocity?
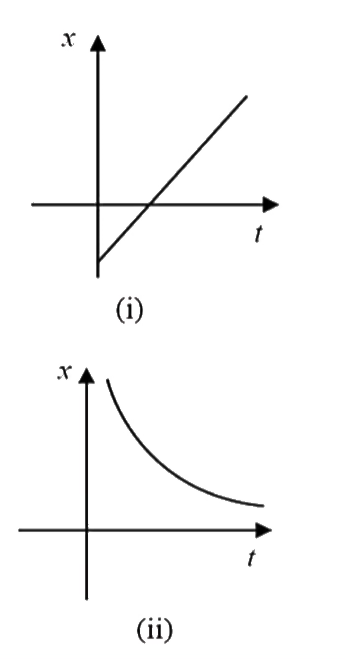
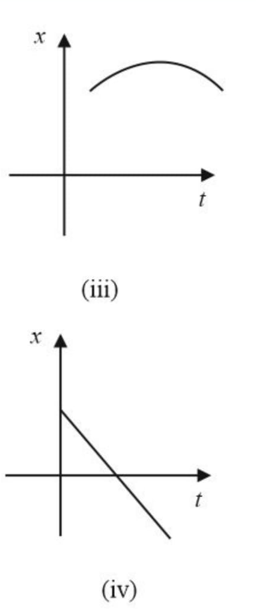 View Solution
View SolutionWhich of the following pairs does not represent the resonance contributors of the same species?
View SolutionWhich of the following pairs does not represent resonance structures?
View SolutionWhich of the following pairs of structures does not represent resonating structures?
View Solution
