The equation of an equipotential line in an electric field is y=2x, then electric field strength vectro at 1,2 may be .
4ˆi+3ˆj
4ˆi+8ˆj
8ˆi+4ˆj
−8ˆi+4ˆj
The correct Answer is:D
To find the electric field strength vector at the point (1, 2) given that the equation of an equipotential line is y=2x, we can follow these steps:
Step 1: Identify the slope of the equipotential line
The equation of the equipotential line is given as y=2x. The slope m1 of this line can be identified directly from the equation.
m1=2
Step 2: Determine the slope of the electric field line
The electric field lines are perpendicular to the equipotential lines. Therefore, the product of their slopes m1 and m2 (the slope of the electric field line) must equal -1.
m1⋅m2=−1
Substituting the value of m1:
2⋅m2=−1
Now, solve for m2:
m2=−12
Step 3: Express the electric field vector in terms of its components
The slope m2 can be expressed in terms of the components of the electric field vector. The electric field vector →E can be represented as:
→E=Ex^i+Ey^j
The slope is given by the ratio of the y component to the x component:
EyEx=m2
Substituting the value of m2:
EyEx=−12
Step 4: Choose suitable values for Ex and Ey
From the ratio EyEx=−12, we can express Ey in terms of Ex:
Ey=−12Ex
Now, we can choose a convenient value for Ex. Let's say Ex=2. Then:
Ey=−12⋅2=−1
Step 5: Write the electric field vector
Thus, the electric field vector at the point (1, 2) can be expressed as:
→E=2^i−1^j
Conclusion
The electric field strength vector at the point (1, 2) is:
→E=2^i−1^j
The equation of the equipotential line is given as y=2x. The slope m1 of this line can be identified directly from the equation.
The electric field lines are perpendicular to the equipotential lines. Therefore, the product of their slopes m1 and m2 (the slope of the electric field line) must equal -1.
The slope m2 can be expressed in terms of the components of the electric field vector. The electric field vector →E can be represented as:
From the ratio EyEx=−12, we can express Ey in terms of Ex:
Thus, the electric field vector at the point (1, 2) can be expressed as:
The electric field strength vector at the point (1, 2) is:
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice-03
Explore 7 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:ASSERTION-REASON
Explore 18 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
For the following electric field lines, the the electric field is
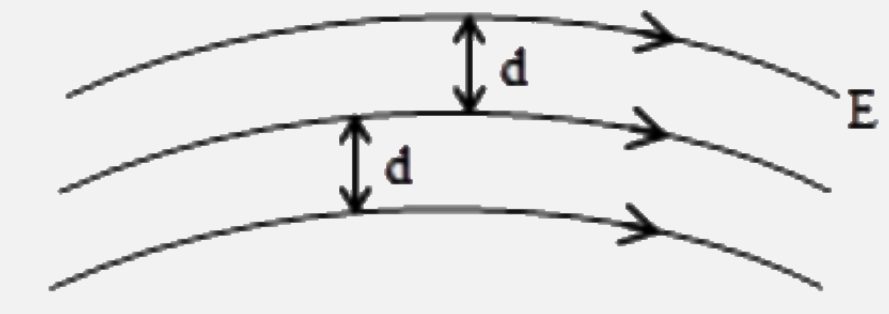
View SolutionThe potentaial function of an electrostatic field is given by V=2x2. Determine the electric field strength at the point (2m,0,3m).
View SolutionEquipotential surfaces are shown in figure. Then the electric field strength will be
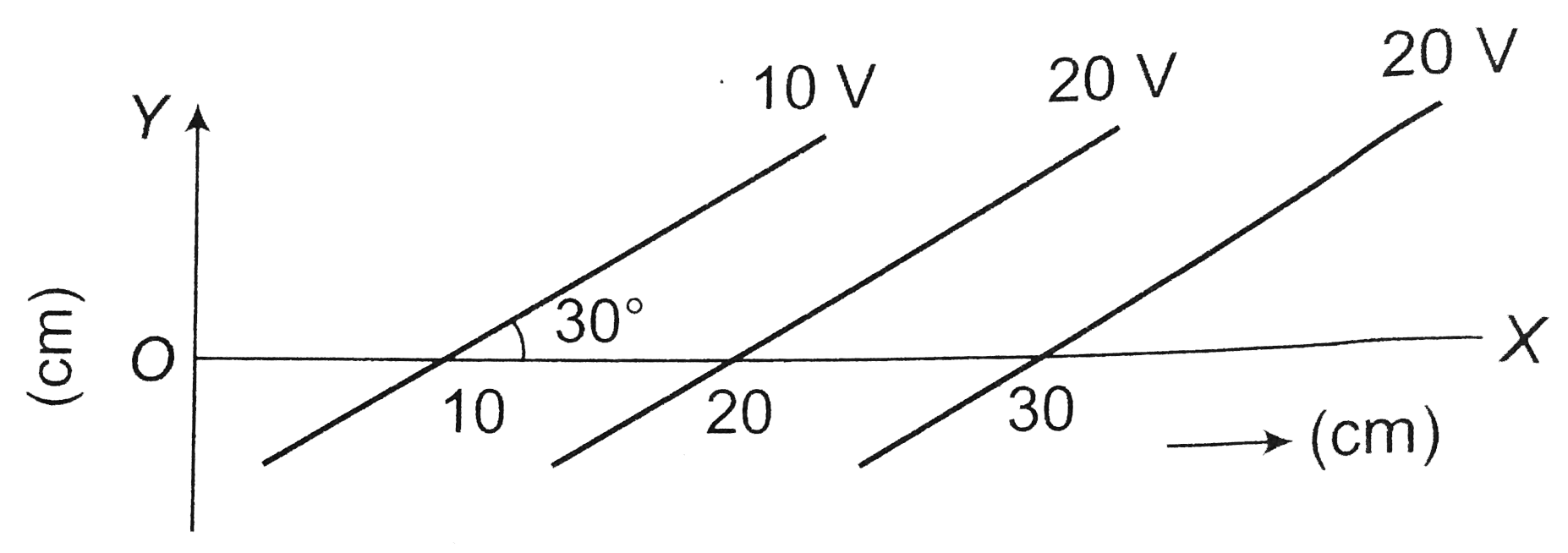
View SolutionIf electric field is uniform, then the electric lines of forces are :
View SolutionThe electric potential in a region is represented as
V=2x+3y−z
obtain expression for electric field strength.
View SolutionThe electric potential in a region is represented as
V=2x+3y−z
obtain expression for electric field strength.
View SolutionA point charge is brought in an electric field. The electric field at a near by point
View SolutionWhat is the angle between the electric dipole moment and the electric field strength due to it on the equatorial line
View SolutionIf the electric potential in a region is represented as V=2x+3y−4z.Then electric field vector will written as
View SolutionIs an electric field of the type shown by the electric lines in fig. physically possible?
 .
.
View Solution

