A particle moves on a given line with a constant speed v. At a certain time it is at point P on its staight line path.O is fixedpoint .show that (Op×v) is independent of the position P.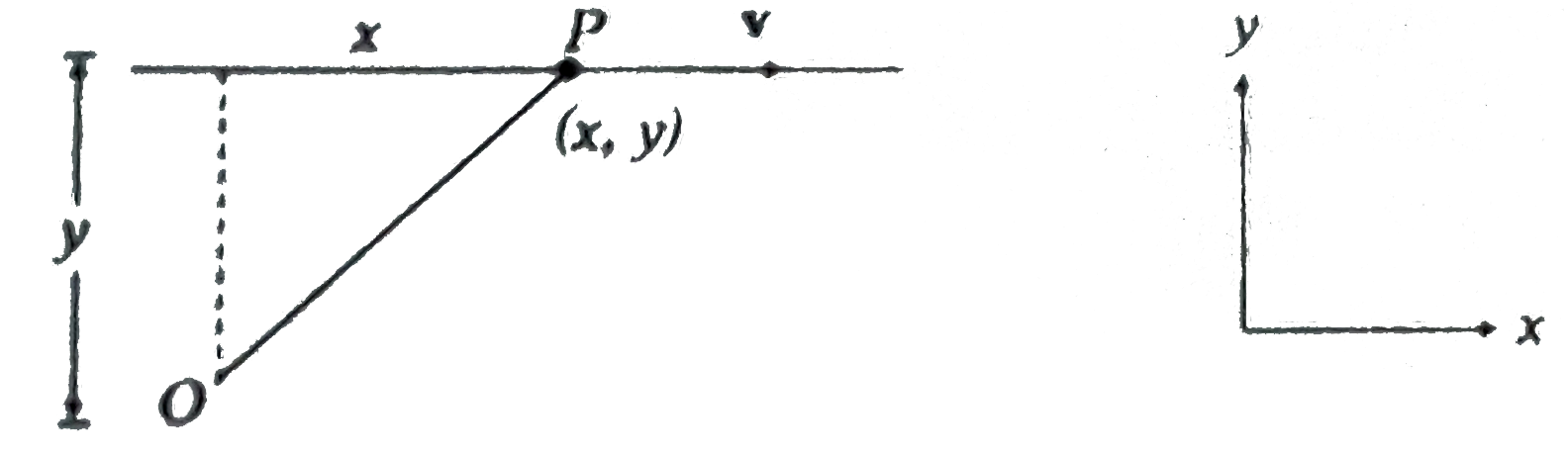
Let →v=vˆi & −−→OP=xˆi+yˆj=xˆi+dˆj

so −−→OP×→v=(xˆi+dˆj)×vˆi=−dvˆk
(d= is constant)
which is independent of position.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)
15 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
19 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-04 [A]
28 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
A particle moves on a given straight line with a constant speed v. At a certain time it is at a point P on its straight lline path.O is a fixed point. Show than −−→OP×→υ is independent of the position P.?
View SolutionA particle moves on a given straight line with a constant speed v. At a certain time it is at a point P on its straight lline path.O is a fixed point. Show than −−→OP×→υ is independent of the position P.?
View Solution
Knowledge Check
A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A particle moves on a given straight line with a constant speed v. At a certain time it is at a point P o its straight lline path.O is a fixed point. Show than −−→OP×→υ is independent of the position P.?
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA particle is moving on a circular path with constant speed, then its acceleration will be constant in
View SolutionA particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
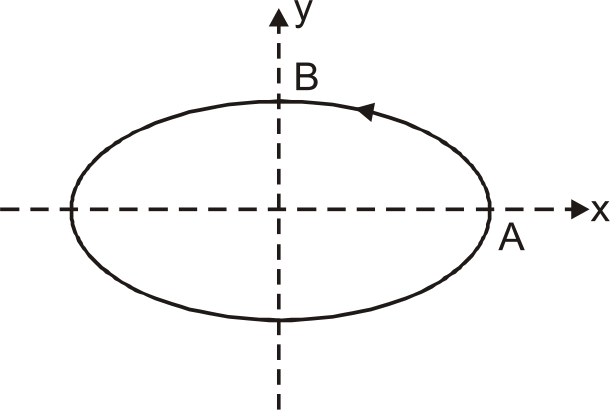
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
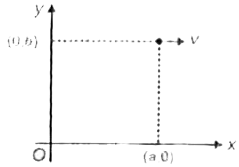
View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
View Solution
